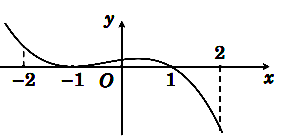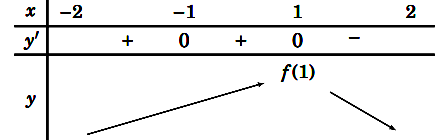Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() và hàm số
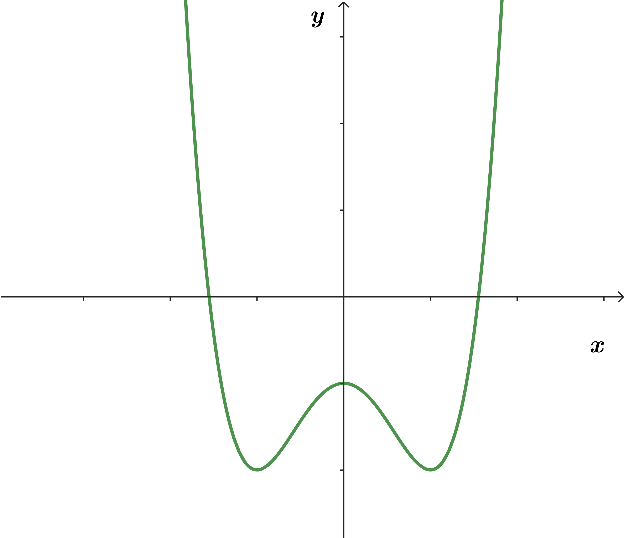
và hàm số ![]() là hàm số bậc ba có đồ thị là đường cong trong hình vẽ. Xét tính đúng sai của các khẳng định sau:
là hàm số bậc ba có đồ thị là đường cong trong hình vẽ. Xét tính đúng sai của các khẳng định sau:

a) Hàm số ![]() đồng biến trên khoảng (−∞; -2). Sai||Đúng
đồng biến trên khoảng (−∞; -2). Sai||Đúng
b) Hàm số ![]() có hai điểm cực trị. Sai||Đúng
có hai điểm cực trị. Sai||Đúng
c) ![]() . Sai||Đúng
. Sai||Đúng
d) Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
Cho hàm số có đạo hàm trên
và hàm số
là hàm số bậc ba có đồ thị là đường cong trong hình vẽ. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng (−∞; -2). Sai||Đúng
b) Hàm số có hai điểm cực trị. Sai||Đúng
c) . Sai||Đúng
d) Hàm số đồng biến trên khoảng
. Đúng||Sai
a) Sai: Vì từ đồ thị của hàm số ta thấy
nên hàm số đồng biến trên khoảng (1; +∞).
b) Sai: Vì từ đồ thị của hàm số ta thấy
chỉ đổi dấu một lần qua x = 1 nên hàm số có một điểm cực trị.
c) Sai: Từ đồ thị ta có hàm số có dạng
Đồ thị hàm số đi qua
nên
Vậy
d) Đúng: Ta có:
Vẽ đường thẳng y = x − 1 trên cùng hệ trục tọa độ với đồ thị hàm số
Khi đó
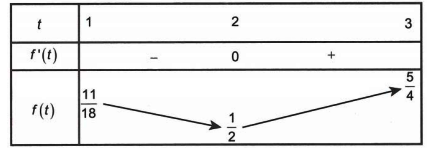
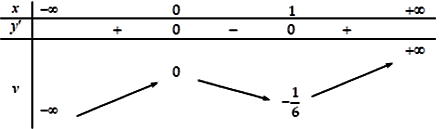
Bảng biến thiên của hàm số g(x) như sau:
Hàm số g(x) đồng biến trên khoảng (−3; -1) nên g(x) đồng biến trên khoảng