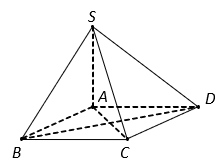
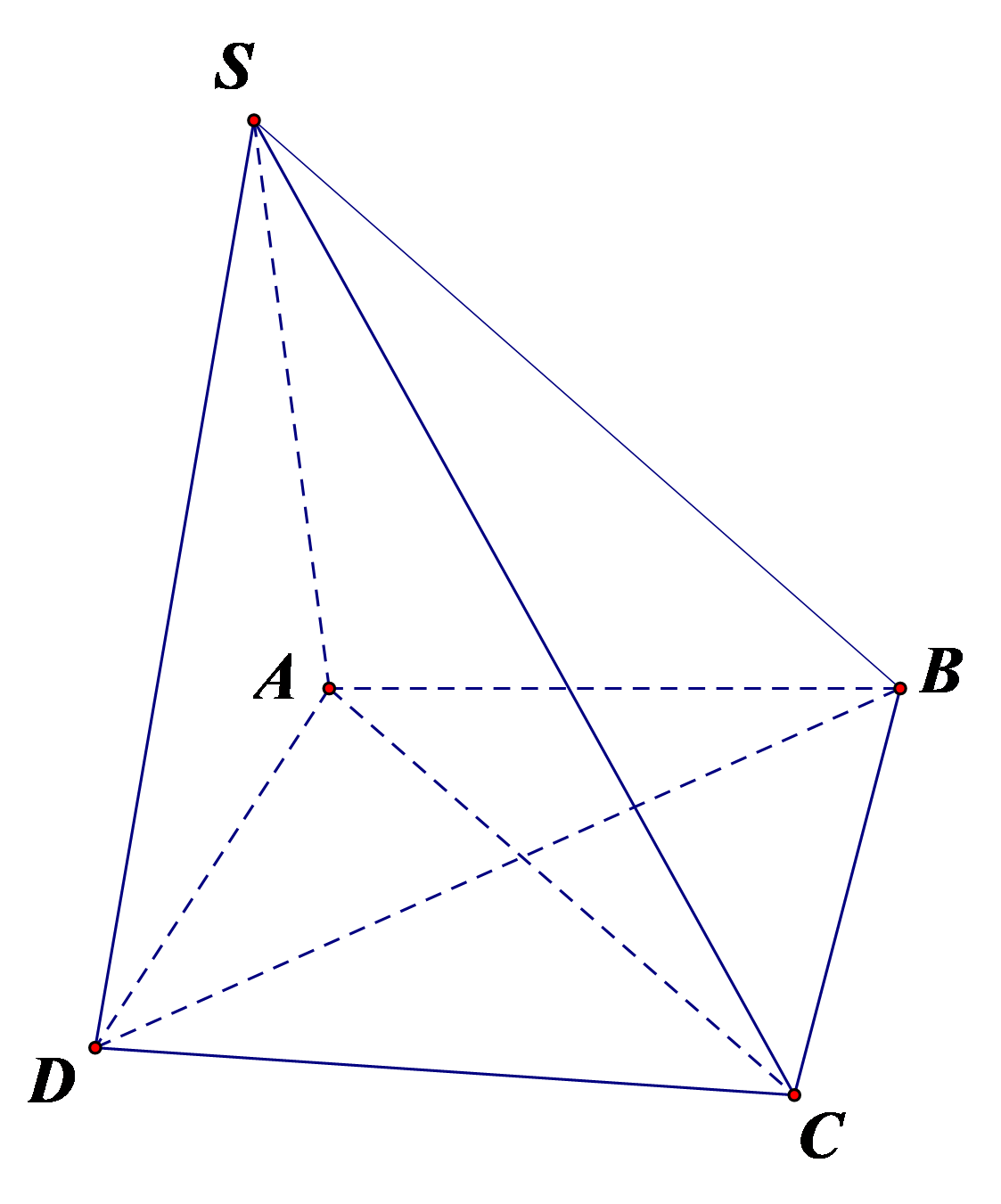
Cho khối chóp S.ABC có SA vuông góc với đáy, ![]() và
và ![]() . Tính thể tích V của khối chóp
. Tính thể tích V của khối chóp ![]() .
.
32
Cho khối chóp S.ABC có SA vuông góc với đáy, và
. Tính thể tích V của khối chóp
.
32
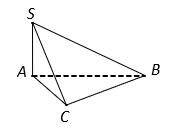
Xét tam giác , có:
Suy ra tam giác vuông tại A
Vậy thể tích khối chóp