Chọn phát biểu đúng về mệnh đề sau: "![]() ,
, ![]() "?
"?
Phát biểu đúng của mệnh đề ",
" là: “Với mọi số tự nhiên x, bình phương của nó đều nhỏ hơn 0”.
Chọn phát biểu đúng về mệnh đề sau: "![]() ,
, ![]() "?
"?
Phát biểu đúng của mệnh đề ",
" là: “Với mọi số tự nhiên x, bình phương của nó đều nhỏ hơn 0”.
Khi x là số lẻ, mệnh đề nào sau đây là mệnh đề sai:
Khi x là số lẻ => “x không chia hết cho 4” là mệnh đề đúng.
Khi x là số lẻ “x không chia hết cho 3” và “x chia hết cho 3” là một khẳng định nhưng không xác định được tính hoặc đúng hoặc sai tùy theo giá trị của x => Không phải mệnh đề.
Khi x là số lẻ “x chia hết cho 2” là mệnh đề sai.
Cho ![]() là tập hợp các số tự nhiên chẵn không lớn hơn
là tập hợp các số tự nhiên chẵn không lớn hơn ![]() ,
, ![]() . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?
Liệt kê các phần tử của tập hợp đã cho ta có kết luận đúng là:
Tìm đáp án không phải mệnh đề trong các câu sau.
Câu “Bộ phim quá hay!” là câu cảm thán nên không phải là mệnh đề.
Cách biểu diễn nào sau đây đúng cho tập số [‒5; 5]
Ta có:
Dấu “[” và “]” kí hiệu cho nửa đoạn trên trục số.
Biểu diễn tập [‒5; 5] trên trục số đúng là:

Điền vào chỗ trống: “Hiệu của tập hợp A và tập hợp B là ….”
Hiệu của tập hợp A và tập hợp B là tập hợp các phần tử thuộc A nhưng không thuộc B.
Tập hợp ![]() có bao nhiêu tập hợp con gồm 2 phần tử:
có bao nhiêu tập hợp con gồm 2 phần tử:
Tập gồm
phần tử.
Mỗi phần tử ghép với phần tử còn lại ta được
tập con của
có
phần tử.
Số tập con của có
phần tử bằng:
Cho biết ![]() là một phần tử của tập hợp
là một phần tử của tập hợp ![]() xét các mệnh đề sau:
xét các mệnh đề sau:
(I) ![]()
(II) ![]() .
.
(III) ![]()
(IV) ![]()
Trong các mệnh đề sau, mệnh đề nào là đúng:
I đúng.
II sai vì không có khái niệm tập hợp này thuộc tập hợp kia.
III sai vì phần tử thì không thể là con của
tập hợp.
IV đúng.
Tìm mệnh đề phủ định của mệnh đề: “Vịt là một loài chim”.
Phủ định của mệnh đề P là mệnh đề “không phải P"
Chọn đáp án Vịt không phải là một loài chim.
Mệnh đề nào sau đây có mệnh đề phủ định là mệnh đề đúng:
Ta có: mệnh đề là mệnh đề sai vì
nên không có bất kì giá trị
nào thỏa mãn
Vì mệnh đề
là mệnh đề sai nên mệnh đề phủ định của nó là mệnh đề đúng.
Chọn đáp án
Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp ![]() .
.
Ta có: .
Cho hai mệnh đề A: “∀ x ∈ R: ![]() ” và B: “∃ n ∈ Z:
” và B: “∃ n ∈ Z: ![]() ”. Xét tính đúng, sai của hai mệnh đề A và B.
”. Xét tính đúng, sai của hai mệnh đề A và B.
Với mệnh đề A, thay nên A sai.
Với mệnh đề B, thay nên B đúng.
Cho tập hợp A = {![]() , với
, với ![]() là số thực dương}. Tìm số nhỏ nhất của tập hợp A?
là số thực dương}. Tìm số nhỏ nhất của tập hợp A?
Ta có:
Đẳng thức xảy ra khi .
Vậy số nhỏ nhất là
Có bao nhiêu mệnh đề trong các câu sau?
Số nguyên dương là số tự nhiên khác 0.
Bạn hãy cố gắng, nhất định bạn sẽ thành công.
Tổng các góc của một tam giác là ![]()
Cố lên, sắp đến nơi rồi!
Câu “Số nguyên dương là số tự nhiên khác 0.” và “Tổng các góc của một tam giác là ” là mệnh đề.
Người ta thường kí hiệu tập hợp số như thế nào?
Người ta thường kí hiệu các tập hợp số như sau:
Xác định ![]() trong trường hợp
trong trường hợp ![]() {
{![]() ,
, ![]() và
và ![]() }, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12.
}, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12.
Liệt kê các phần tử ta có:
Vậy .
Cho ![]()
![]() Tập hợp
Tập hợp ![]() bằng
bằng
Tập hợp gồm những phần tử thuộc
nhưng không thuộc
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp ![]()
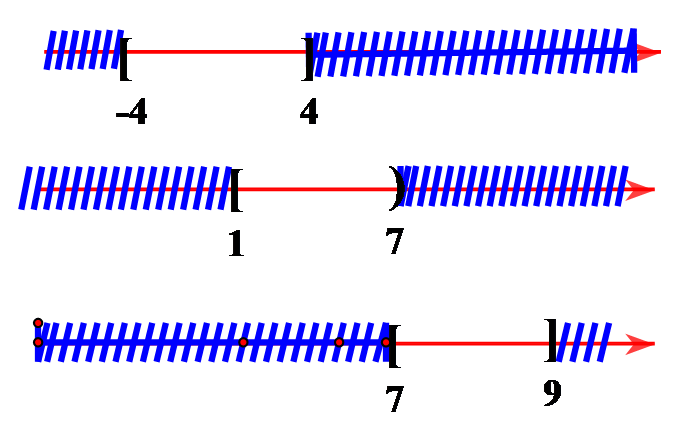
Vậy .
Trong các mệnh đề sau, mệnh đề nào sai?
Xét mệnh đề . Ta thấy
sai nên mệnh đề này sai.
Số tập hợp con có 2 phần tử của tập hợp ![]() là:
là:
Các tập hợp con của tập hợp là:
Có tất cả 15 tập con của tập hợp A.
