Cho A = {a, b}. Số tập con của A là:
Ta có: Số tập hợp con của tập có phần tử là
. Do đó số tập con của A là
.
Cho A = {a, b}. Số tập con của A là:
Ta có: Số tập hợp con của tập có phần tử là
. Do đó số tập con của A là
.
Trong định lí ta nói: "P là điều kiện cần để có Q". Khi đó P là gì của định lí?
Trong định lí ta nói: " là điều kiện cần để có
". Khi đó P là kết luận của định lí.
Với giá trị thực nào của ![]() mệnh đề chứa biến
mệnh đề chứa biến ![]() là mệnh đề đúng?
là mệnh đề đúng?
Thay vào
ta được
là mệnh đề đúng.
Tập ![]() bằng tập nào sau đây?
bằng tập nào sau đây?
Có bao nhiêu câu là mệnh đề trong các câu sau:
(1) Môn toán khó quá!
(2) Bạn có đói không?
(3) ![]() hoặc
hoặc ![]()
(4) ![]()
Câu (1) là câu cảm thán, câu (2) là câu nghi vấn nên không phải mệnh đề.
Các câu còn lại là mệnh đề.
Có
câu là mệnh đề.
Tìm điều kiện cần và đủ để hai khoảng ![]() và
và ![]() là tập rỗng, biết
là tập rỗng, biết ![]() là số thực âm.
là số thực âm.
Điều kiện cần và đủ để hai tập giao khác rỗng là:
Mệnh đề nào sau đây là đúng?
nhưng
sai.
nhưng
sai.
nhưng
sai.
Cho mệnh đề: “Một tứ giác là hình thang cân khi và chỉ khi tứ giác đó có hai đường chéo bằng nhau”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?
Mệnh đề tương đương với mệnh đề đã cho là: Điều kiện cần và đủ để một tứ giác có hai đường chéo bằng nhau là tứ giác đó là một hình thang cân.
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo ĐÚNG?
Nếu a chia hết cho 3 thì a chia hết cho 9 có mệnh đề đảo là Nếu a chia hết cho 9 thì a chia hết cho 3. Đây là mệnh đề đảo đúng.
Khi x là số lẻ, mệnh đề nào sau đây là mệnh đề sai:
Khi x là số lẻ => “x không chia hết cho 4” là mệnh đề đúng.
Khi x là số lẻ “x không chia hết cho 3” và “x chia hết cho 3” là một khẳng định nhưng không xác định được tính hoặc đúng hoặc sai tùy theo giá trị của x => Không phải mệnh đề.
Khi x là số lẻ “x chia hết cho 2” là mệnh đề sai.
Xác định tập hợp ![]()
Xác định kết quả tập hợp bằng hình vẽ như sau:
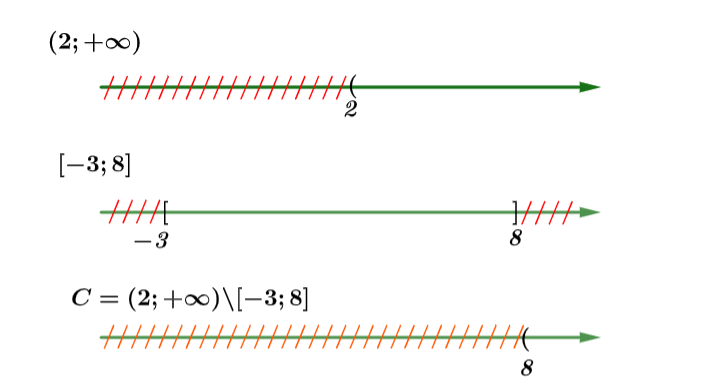
Vậy
Phủ định của mệnh đề “Phương trình ![]() có 2 nghiệm phân biệt” là mệnh đề nào?
có 2 nghiệm phân biệt” là mệnh đề nào?
Phủ định của mệnh đề P là mệnh đề "không phải P".
Chọn đáp án Phương trình không phải có 2 nghiệm phân biệt.
Cho tập hợp ![]() và
và ![]() Tập hợp
Tập hợp ![]() bằng tập nào sau đây?
bằng tập nào sau đây?
Tập hợp gồm những phần tử thuộc
nhưng không thuộc
.
Tìm phát biểu là mệnh đề.
Ta có:
Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai của nó. Một mệnh đề không thể vừa đúng, vừa sai.
Suy ra “Hà Nội là thủ đô của Việt Nam.” là mệnh đề.
Cho mệnh đề chứa biến ![]() chia hết cho 4” với
chia hết cho 4” với ![]() là số nguyên. Xét xem các mệnh đề
là số nguyên. Xét xem các mệnh đề ![]() và
và ![]() đúng hay sai?
đúng hay sai?
Thay và
vào
ta được các số
và
không chia hết cho
. Vậy
đúng và
sai.
Trong các mệnh đề sau tìm mệnh đề đúng?
Với thì
mệnh đề
là mệnh đề đúng.
Chọn đáp án
Người ta thường kí hiệu tập hợp số như thế nào?
Người ta thường kí hiệu các tập hợp số như sau:
Cho hai tập hợp: X = ![]() là bội của
là bội của ![]() và
và ![]() và Y=
và Y= ![]() n là bội số của 12}
n là bội số của 12}
Trong các mệnh đề nào sau đây, mệnh đề nào là sai?
là bội của
và
là số tự nhiên chia hết cho
và
chia hết cho
Tập hợp các số tự nhiên chia hết cho
là bội của
chia hết cho
Tập hợp các số tự nhiên chia hết cho
đáp án sai là
và
Cho ![]() và
và ![]() Khi đó:
Khi đó:
Ta có:
Khẳng định nào đúng trong các khẳng định sau:
Khẳng định đúng: "Nếu và
thì
"
