Lớp 12 Toán 12 - Chân trời sáng tạo

Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST

Mô tả thêm: Bài kiểm tra 15 phút Ứng dụng đạo hàm để khảo sát hàm số của chúng tôi gồm 4 mức độ được thay đổi ngẫu nhiên, giúp bạn đọc rèn luyện củng cố kiến thức tốt hơn.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho hàm số y = - x^{3} - 3(m + 1)x^{2} + 3(2m - 1)x + 2020. Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên ( - \infty; + \infty)?

    Ta có: y' = - 3x^{2} - 6(m + 1)x + 3(2m - 1)

    Để hàm số đã cho nghịch biến trên ( - \infty; + \infty)

    \Leftrightarrow y' \leq 0 \Leftrightarrow \Delta' \leq 0

    \Leftrightarrow 9\left( m^{2} + 2m + 1 ight) + 18m - 9 \leq 0

    \Leftrightarrow 9m^{2} + 36m \leq 0 \Leftrightarrow - 4 \leq m \leq 0

    Do m\mathbb{\in Z} nên có tất cả 5 giá trị của m thỏa mãn điều kiện.

  • Câu 2: Thông hiểu

    Biết rằng có hai giá trị t_{1};t_{2} của tham số t để đường thẳng y = t - x và đồ thị hàm số y = \frac{x}{x - 1} có đúng một điểm chung. Khẳng định nào sau đây đúng?

    Phương trình hoành độ giao điểm t - x = \frac{x}{x - 1} \Leftrightarrow (t - x)(x - 1) = x

    \Leftrightarrow x^{2} - tx + t = 0(*)

    Đường thẳng y = t - x và đồ thị hàm số y = \frac{x}{x - 1} có một điểm chung khi phương trình (*) có 1 nghiệm duy nhất

    \Leftrightarrow \Delta = 0 \Leftrightarrow t^{2} - 4t = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = 4 \\ \end{matrix} ight.

    Vậy t_{1} + t_{2} = 4 \in \left( - 1;\frac{9}{2} ight).

  • Câu 3: Thông hiểu

    Cho hàm số y = 2x^{3} - 3x^{2} - m. Trên đoạn \lbrack - 1;1brack hàm số có giá trị nhỏ nhất là - 1. Tìm giá trị của m?

    Ta có: y' = 6x^{2} - 6x \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight.

    Ta có bảng biến thiên như sau:

    Từ bảng biến thiên suy ra \min_{\lbrack - 1;1brack}y = - 5 - m \Leftrightarrow - 1 = - 5 - m \Leftrightarrow m = - 4.

    Vậy m = - 4 là giá trị cần tìm.

  • Câu 4: Thông hiểu

    Hàm số y = f(x) có đạo hàm và liên tục trên \mathbb{R}. Hàm số y = f'(1 - x) có đồ thị như hình vẽ:

    Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?

    Hàm số y = f(x) nghịch biến

    \Leftrightarrow f'(x) < 0 \Leftrightarrow f'(1 - t) < 0 với x = 1 - t

    \Leftrightarrow \left\lbrack \begin{matrix} t < 0 \\ 1 < t < 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} 1 - x < 0 \\ 1 < 1 - x < 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x > 1 \\ - 1 < x < 0 \\ \end{matrix} ight.

    Vậy hàm số y = f(x) nghịch biến trên khoảng ( - 1;0).

  • Câu 5: Nhận biết

    Cho hàm số y = f(x) có đồ thị như hình vẽ.

    Đồ thị hàm số đã cho có đường tiệm cận ngang bằng:

    Dựa vào đồ thị hàm số ta có: \lim_{x ightarrow \pm \infty}f(x) = - 1.

    Do đó, đồ thị hàm số y = f(x) có đường tiệm cận ngang là y = - 1.

  • Câu 6: Nhận biết

    Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ?

    Dựa vào hình dáng đồ thị ta suy ra đồ thị của hàm số bậc 4 có hệ số a > 0.

    Vậy hàm số cần tìm là y = x^{4} - x^{2} - 1.

  • Câu 7: Thông hiểu

    Sự ảnh hưởng khi sử dụng một loại thuốc với cá thể X được một nhà sinh học mô tả bởi hàm số P(t) = \frac{t + 1}{t^{2} + t + 4}, trong đó P(t) là số lượng cá thể sau t giờ sử dụng thuốc. Vào thời điểm nào thì số lượng cá thể X bắt đầu giảm?

    Xét P(t) = \frac{t + 1}{t^{2} + t + 4} ta có: P'(t) = \frac{- t^{2} - 2t + 3}{\left( t^{2} + t + 4 ight)^{2}} = \frac{(t - 1)( - t - 3)}{\left( t^{2} + t + 4 ight)^{2}}

    P'(t) = 0 \Leftrightarrow \frac{(t - 1)( - t - 3)}{\left( t^{2} + t + 4 ight)^{2}} = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = - 3 \\ t = 1 \\ \end{matrix} ight.

    Ta thấy hàm số đạt cực đại tại t = 1 và P'(t) < 0;\forall t \in (1; + \infty) nên sau 1 giờ thì cá thể bắt đầu giảm.

  • Câu 8: Vận dụng

    Cho hàm số y = f(x) có bảng biến thiên như hình vẽ:

    Hàm số g(x) = f\left( 2x^{2} - \frac{5}{2}x - \frac{3}{2} ight) nghịch biến trong khoảng nào dưới đây?

    Ta có:

    g'(x) = \left( 4x - \frac{5}{2} ight).f'\left( 2x^{2} - \frac{5}{2}x - \frac{3}{2} ight)

    Xét g'(x) = 0 \Leftrightarrow\left\lbrack \begin{matrix}4x - \dfrac{5}{2} = 0 \\f'\left( 2x^{2} - \dfrac{5}{2}x - \dfrac{3}{2} ight) = 0 \\\end{matrix} ight.

    \Leftrightarrow \left\lbrack\begin{matrix}x = \dfrac{5}{8} \\2x^{2} - \dfrac{5}{2}x - \dfrac{3}{2} = - 2 \\2x^{2} - \dfrac{5}{2}x - \dfrac{3}{2} = 3 \\\end{matrix} ight.\ \Leftrightarrow x \in \left\{ -1;\dfrac{1}{4};\dfrac{5}{8};1;\dfrac{9}{4} ight\}

    Ta có bảng xét dấu:

    g'(0) = - \frac{5}{2}.f'\left( - \frac{3}{2} ight) > 0 \Rightarrow g'(x) > 0;\forall x \in \left( - 1;\frac{1}{4} ight)

    Vậy đáp án cần tìm là \left( 1;\frac{5}{4} ight).

  • Câu 9: Nhận biết

    Cho hàm số có đạo hàm f'(x) = (x + 2)^{3}(x - 2)^{3}(3 - x). Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

    Ta có: f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 \\ x = 2 \\ x = 3 \\ \end{matrix} ight. ta có bảng xét dấu như sau:

    Vậy hàm số đồng biến trên khoảng (2;3).

  • Câu 10: Vận dụng

    Cho đồ thị hàm số (C):y = \frac{2x + 1}{x + 2}. Giả sử M(a;b) \in (C) có khoảng cách đến đường thẳng d:y = 3x + 6 nhỏ nhất. Chọn khẳng định đúng?

    Ta có: M\left( a;\frac{2a + 1}{a + 2} ight);(a eq - 2)

    Khoảng cách từ M đến đường thẳng (d) bằng:

    d(M;d) = \dfrac{\left| 3a - \dfrac{2a +1}{a + 2} + 6 ight|}{\sqrt{3^{2} + 1}}= \frac{1}{\sqrt{10}}.\left| 3a+ 6 - \frac{2a + 1}{a + 2} ight|= \frac{1}{\sqrt{10}}.\left|\frac{3a^{2} + 10a + 11}{a + 2} ight|

    Xét hàm số f(a) = \frac{3a^{2} + 10a + 11}{a + 2};(a eq - 2)

    f'(a) = \frac{3\left( a^{2} + 4a + 3 ight)}{(a + 2)^{2}} = 0 \Leftrightarrow \left\lbrack \begin{matrix} a = - 1 \\ a = - 3 \\ \end{matrix} ight.

    Ta có bảng biến thiên

    Vậy giá trị nhỏ nhất của hàm số \left| f(a) ight| = 4 tại a = - 1

    Vậy \left\{ \begin{matrix} a = - 1 \\ b = - 1 \\ \end{matrix} ight.\ \Rightarrow a + b = - 2

  • Câu 11: Nhận biết

    Cho hàm số f(x) có bảng xét dấu của đạo hàm f'(x) như sau:

    Hàm số f(x) có bao nhiêu điểm cực trị?

    Dựa vào bảng xét dấu ta thấy hàm số có bốn điểm cực trị.

  • Câu 12: Nhận biết

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có bảng xét dấu của f'(x) như sau:

    Số điểm cực tiểu của hàm số đã cho là

    Đạo hàm f'(x) đổi dấu từ âm sang dương hai lần qua các điểm x = - 2 và x = 2 nên hàm số đã cho có hai điểm cực tiểu.

  • Câu 13: Vận dụng

    Cho hàm số f(x) có đạo hàm trên \mathbb{R} và thỏa mãn f(x) > f'(x) + 1;\forall x\mathbb{\in R}. Bất phương trình f(x) < me^{x} + 1 nghiệm đúng với mọi x \in (0; + \infty) khi và chỉ khi

    Ta có:

    f(x) < me^{x} + 1 \Leftrightarrow f(x) - 1 < me^{x}

    \Leftrightarrow \frac{f(x) - 1}{e^{x}} < m.

    Xét hàm số g(x) = \frac{f(x) - 1}{e^{x}} có

    g'(x) = \frac{f'(x) - \left\lbrack f(x) - 1 ightbrack}{e^{x}} < 0;\forall x \in (0; + \infty)

    Bảng biến thiên

    Vậy bất phương trình f(x) < me^{x} + 1 nghiệm đúng với mọi x \in (0; + \infty) khi và chỉ khi m \geq f(0) - 1.

  • Câu 14: Nhận biết

    Các dân tộc ít người phân bố chủ yếu ở khu vực nào của Trung Quốc?

  • Câu 15: Thông hiểu

    Đường tiệm cận xiên của đồ thị hàm số y = \frac{x^{2} - 2x + 3}{x + 1} là đường thẳng có phương trình

    Tập xác định: D = R\backslash\left\{ - 1 ight\}.

    Phương trình đường tiệm cận xiên có dạng: y = ax + b.

    Trong đó,

    a = \lim_{x ightarrow + \infty}\frac{f(x)}{x} = \lim_{x ightarrow + \infty}\frac{x^{2} - 2x + 3}{x^{2} + x} = 1

    b = \lim_{x ightarrow + \infty}\left\lbrack f(x) - ax ightbrack = \lim_{x ightarrow + \infty}\left( \frac{x^{2} - 2x + 3}{x + 1} - x ight) = \lim_{x ightarrow + \infty}\frac{- 3x + 3}{x + 1} = - 3.

    Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x - 3.

  • Câu 16: Nhận biết

    Số đường tiệm cận ngang của đồ thị hàm số y = \frac{x}{\sqrt{x^{2} + 1}} bằng:

    Ta có:

    \lim_{x ightarrow + \infty}y = \lim_{x ightarrow + \infty}\left( \frac{x}{\sqrt{x^{2} + 1}} ight) = 1 suy ra y = 1 là một tiệm cận ngang của đồ thị hàm số.

    \lim_{x ightarrow - \infty}y = \lim_{x ightarrow - \infty}\left( \frac{x}{\sqrt{x^{2} + 1}} ight) = - 1 suy ra y = - 1 là một tiệm cận ngang của đồ thị hàm số.

    Vậy tổng số đường tiệm cận ngang của đồ thị hàm số đã cho bằng 2.

  • Câu 17: Thông hiểu

    Cho hàm số y = \frac{{{x^2} + 3}}{{x - 1}}. Khẳng định nào sau đây đúng?

    Tập xác định D = \mathbb{R}\backslash \left\{ 1 ight\}

    \begin{matrix} y' = \dfrac{{{x^2} - 2x - 3}}{{{{\left( {x - 1} ight)}^2}}} \hfill \\ y' = 0 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - 1} \\ {x = 3} \end{array}} ight. \hfill \\ y'' = \frac{8}{{{{\left( {x - 1} ight)}^3}}} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {y''\left( { - 1} ight) = - 1 < 0} \\ {y''\left( 3 ight) = 1 > 0} \end{array}} ight. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{y_{CD}} = y\left( { - 1} ight) = - 2} \\ {{y_{CT}} = y\left( 3 ight) = 3} \end{array}} ight. \Rightarrow {y_{CD}} < {y_{CT}} \hfill \\ \end{matrix}

  • Câu 18: Vận dụng cao

    Cho hàm số f\left( x ight) = a{x^4} + b{x^3} + c{x^2} + dx + e,\left( {a e 0} ight) có đồ thị của đạo hàm f’(x) như hình vẽ:

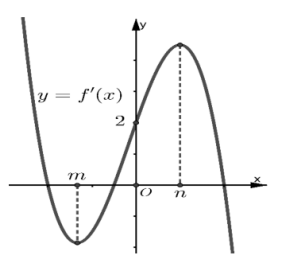
    Xác định số điểm cực trị của hàm số

    Biết rằng e > n. Số điểm cực trị của hàm số y = f'\left( {f\left( x ight) - 2x} ight) bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số f\left( x ight) = a{x^4} + b{x^3} + c{x^2} + dx + e,\left( {a e 0} ight) có đồ thị của đạo hàm f’(x) như hình vẽ:

    Xác định số điểm cực trị của hàm số

    Biết rằng e > n. Số điểm cực trị của hàm số y = f'\left( {f\left( x ight) - 2x} ight) bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 19: Nhận biết

    Điểm nào sau đây thuộc đồ thị hàm số y = x^{3} - 3x?

    Thay (1; - 2) vào y = x^{3} - 3x ta được:

    - 2 = 1^{3} - 3.1

    Vậy (1; - 2) thuộc đồ thị hàm số y = x^{3} - 3x.

  • Câu 20: Nhận biết

    Hàm số y = f(x) liên tục trên đoạn \lbrack - 1;3brack và có bảng biến thiên như sau.

    Gọi M và m lần lượt là GTLN và GTNN của hàm số trên \lbrack - 1;3brack. Xét tính đúng sai của các khẳng định sau:

    a) m = f(2) Sai|| Đúng

    b) M = f(4) Sai|| Đúng

    c) m = f( - 1) Đúng||Sai

    d) M = f(0) Đúng||Sai

    Đáp án là:

    Hàm số y = f(x) liên tục trên đoạn \lbrack - 1;3brack và có bảng biến thiên như sau.

    Gọi M và m lần lượt là GTLN và GTNN của hàm số trên \lbrack - 1;3brack. Xét tính đúng sai của các khẳng định sau:

    a) m = f(2) Sai|| Đúng

    b) M = f(4) Sai|| Đúng

    c) m = f( - 1) Đúng||Sai

    d) M = f(0) Đúng||Sai

    Dựa vào bảng biến thiên trên \lbrack - 1;3brack ta có:

    m = f( - 1) = 0

    M = f(0) = 5

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 10 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập