Cho hàm số y = f(x) có đạo hàm. Biết f(x) có đạo hàm f’(x) và hàm số y = f’(x) có đồ thị như hình vẽ:

Hàm số g(x) = f(x - 1) đạt cực đại tại điểm nào dưới đây?
Cách 1: Ta có:
Vậy chọn đáp án B
Cách 2: Đồ thị hàm số g’(x) = f’(x – 1) là phép tịnh tiến đồ thị hàm số y = f’(x) theo phương trục hoành sang bên phải 1 đơn vị. Ta có hình vẽ minh họa:
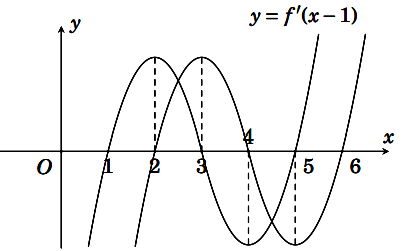
Đồ thị hàm số g’(x) = f’(x – 1) cắt trục hoành tạo các điểm có hoành độ x = 2, x = 4, x = 6 và giá trị hàm số g’(x) đổi dấu từ dương sang âm khi qua điểm x = 4
Chọn B