Lớp 10 Toán 10 - Chân trời sáng tạo

Đề kiểm tra 15 phút Chương 3 Hàm số bậc hai và đồ thị CTST

Mô tả thêm: Đề kiểm tra 15 phút Toán 10 Hàm số bậc hai và đồ thị gồm 20 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Chân trời sáng tạo.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Tập xác định của hàm số y = \frac{3x-1}{2x-2} là:

     Điều kiện xác định: 2x-2 eq 0 \Leftrightarrow x eq 1. Suy ra D= \mathbb {R} \setminus \{1\}.

  • Câu 2: Thông hiểu

    Tập xác định của hàm số f(x) = \sqrt{3 - x} + \frac{1}{\sqrt{x - 1}} là

    Hàm số xác định khi \left\{ \begin{matrix} 3 - x \geq 0 \\ x - 1 > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \leq 3 \\ x > 1 \\ \end{matrix} ight.\ \Leftrightarrow 1 < x \leq 3.

    Vậy tập xác định của hàm số là D = (1; 3].

  • Câu 3: Thông hiểu

    Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ − 7; 7] để phương trình mx2 − 2(m+2)x + m − 1 = 0 có hai nghiệm phân biệt?

    TH1:m = 0 \Leftrightarrow - 4x - 1 = 0 \Leftrightarrow x = - \frac{1}{4}; phương trình chỉ có một nghiệm duy nhất nên loại m = 0

    TH2: m ≠ 0

    Để mx2 − 2(m+2)x + m − 1 = 0với m ∈ [ − 7; 7]có hai nghiệm phân biệt thì

    \Delta' = (m + 2)^{2} - m(m - 1) > 0 \Leftrightarrow 5m > - 4 \Leftrightarrow m > - \frac{4}{5}đồng thời m ∈ [ − 7; 7].

    Vậy m = {1; 2;3;4;5;6;7}→ có 7 giá trị nguyên của m thỏa mãn.

  • Câu 4: Thông hiểu

    Cho hàm số: y = f(x) = |2x-3|. Tìm x để f(x) = 3

    Ta có:

    \begin{matrix} f\left( x ight) = 3 \hfill \\ \Leftrightarrow \left| {2x - 3} ight| = 3 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {2x - 3 = 3} \\ {2x - 3 = - 3} \end{array}} ight. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 3} \\ {x = 0} \end{array}} ight. \hfill \\ \end{matrix}

    Vậy x = 3 hoặc x = 0

  • Câu 5: Nhận biết

    Hàm số y = 2x2 + 4x − 1

    Hàm số y = ax2 + bx + c với a > 0 đồng biến trên khoảng \left( - \frac{b}{2a}; + \infty ight), nghịch biến trên khoảng \left( - \infty; - \frac{b}{2a} ight).

    Áp dụng: Ta có - \frac{b}{2a} = - 1. Do đó hàm số nghịch biến trên khoảng (−∞;−1) và đồng biến trên khoảng (−1;+∞).

  • Câu 6: Nhận biết

    Tìm m để hàm số y = mx +(m+2)x-2 luôn đồng biến biến trên tập số thực.

    Để hàm số y = mx +(m+2)x-2 nghịch biến trên tập số thực thì m>0.

  • Câu 7: Vận dụng cao

    Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x4 − 4x3 − x2 + 10x − 3 trên đoạn [−1; 4] là

    Ta có y = x4 − 4x3 − x2 + 10x − 3 = x4 − 4x3 + 4x2 − 5x2 + 10x − 5 + 2

     = (x2−2x)2 − 5(x−1)2 + 2 = [(x−1)2−1]2 − 5(x−1)2 + 2.

    Đặt t = (x−1)2, x ∈ [−1; 4] ⇒ t ∈ [0; 9].

    y = (t - 1)^{2} - 5t + 2 = t^{2} - 7t + 3= \left( t - \frac{7}{2} ight)^{2} - \frac{37}{4}.

    Cách 1: Ta có 0 \leq \left( t -\frac{7}{2} ight)^{2} \leq \frac{121}{4} \Leftrightarrow -\frac{37}{4} \leq y \leq 21.

    Cách 2: Vẽ BBT

    Description: Capture

    Vậy y_{\min} = - \frac{37}{4}, ymax = 21.

  • Câu 8: Thông hiểu

    Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?

    Nhận xét:

    Bảng biến thiên có bề lõm hướng xuống. Loại đáp án y = 2x2 + 2x − 1 và y = 2x2 + 2x + 2.

    Đỉnh của parabol có tọa độ là \left( - \frac{1}{2};\frac{3}{2} ight). Xét các đáp án, y =  − 2x2 − 2x + 1 thỏa mãn.

  • Câu 9: Thông hiểu

    Cho hàm số: y = \left\{ \begin{matrix} \frac{1}{x - 1} & x \leq 0 \\ \sqrt{x + 2} & x > 0 \\ \end{matrix} ight.. Tập xác định của hàm số là tập hợp nào sau đây?

    Với x ≤ 0 ta có: y = \frac{1}{x - 1} xác định với mọi x ≠ 1 nên xác định với mọi x ≤ 0.

    Với x > 0 ta có: y = \sqrt{x + 2} xác định với mọi x ≥  − 2 nên xác định với mọi x > 0.

    Vậy tập xác định của hàm số là D = ℝ.

  • Câu 10: Nhận biết

    Tìm tọa độ đỉnh S của parabol: y = {x^2} - 2x + 1?

    Gọi tọa độ đỉnh của parabol là điểm I(x; y)

    Hàm số bậc hai có: a = 1;b' = - 1;c = 1

    => \Rightarrow \Delta = b{'^2} - ac = 0

    \left\{ {\begin{array}{*{20}{c}} {x = - \dfrac{b'}{{a}} = - \dfrac{{ - 2}}{{2.1}} = 1} \\ {y = - \dfrac{\Delta' }{{a}} = 0} \end{array}} ight. \Rightarrow I\left( {1;0} ight)

  • Câu 11: Nhận biết

    Hàm số nào sau đây nghịch biến trên khoảng (−∞;0)?

    Xét đáp án y = \sqrt{2}x^{2} + 1, ta có - \frac{b}{2a} = 0 và có a > 0 nên hàm số đồng biến trên khoảng (0;+∞) và nghịch biến trên khoảng (−∞;0).

  • Câu 12: Nhận biết

    Cho hàm số y = f(x) = |-5x|. Khẳng định nào sau đây là sai?

    Ta có: f(\frac{1}{5})=|-5.\frac{1}{5}|=1 e-1

    Khẳng định sai là: f(\frac{1}{5})=-1

  • Câu 13: Vận dụng

    Cho parabol như hình vẽ:

    Có bao nhiêu giá trị nguyên của tham số m với m \in \lbrack 0;3000brack để phương trình f(x) + m = 2022 có hai nghiệm x_{1};x_{2} phân biệt?

    Ta có:

    f(x) + m = 2022 \Leftrightarrow f(x) = - m + 2022(*)

    Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số y = f(x) và y = - m + 2022

    Do đó phương trình (*) có có hai nghiệm phân biệt khi và chỉ khi - m + 2022 < 2 \Leftrightarrow m > 2020.

    Mặt khác m \in \lbrack 0;3000brack suy ra có 980 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 14: Thông hiểu

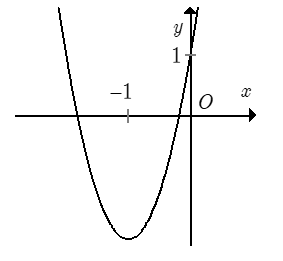
    Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

    Nhận xét:

    Parabol có bề lõm hướng xuống.

    Parabol cắt trục hoành tại 2 điểm (3;0) và (−1;0). Xét các đáp án, đáp án y = - \frac{1}{2}x^{2} + x + \frac{3}{2} thỏa mãn.

  • Câu 15: Vận dụng

    Cho hai hàm số y1 = x2 + (m−1)x + m, y2 = 2x + m + 1. Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì m có giá trị là

    Phương trình hoành độ giao điểm: x2 + (m−1)x + m = 2x + m + 1 ⇔ x2 + (m−3)x − 1 = 0  (1).

    Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì pt(1) có hai nghiệm phân biệt

     ⇔ Δ = (m−3)2 + 4 > 0 luôn đúng ∀m ∈ ℝ.

  • Câu 16: Nhận biết

    Hàm số nào sau đây nghịch biến trên khoảng (−1;+∞)?

    Xét đáp án y = - \sqrt{2}(x + 1)^{2}, ta có y = - \sqrt{2}(x + 1)^{2} = - \sqrt{2}x^{2} - 2\sqrt{2}x - \sqrt{2} nên - \frac{b}{2a} = - 1 và có a < 0 nên hàm số đồng biến trên khoảng (−∞;−1) và nghịch biến trên khoảng (−1;+∞).

  • Câu 17: Nhận biết

    Trong các hàm số sau, hàm số nào là nghịch biến:

    Ta có: 

    Hàm số y = f(x) = -2x + 2 có a = -2 < 0

    => Hàm số nghịch biến.

  • Câu 18: Nhận biết

    Tập xác định của hàm số y = \frac{2 - x}{x^{2} - 4x} là:

    Hàm số xác định \Leftrightarrow x^{2} - 4x eq 0 \Leftrightarrow \left\{ \begin{matrix} x eq 0 \\ x eq 4 \\ \end{matrix} ight.. Vậy D = ℝ ∖ {0;4}.

  • Câu 19: Thông hiểu

    Giả sử đồ thị parabol (P):y = 2x^{2} + bx + c đi qua điểm A(0;4) và có trục đối xứng là đường thẳng x - 1 = 0. Tính tổng các giá trị b và c?

    Ta có: A \in (P) \Rightarrow c = 4

    Trục đối xứng của (P) là: - \frac{b}{2a} = 1 \Leftrightarrow b = - 4

    \Rightarrow b + c = - 4 + 4 = 0

  • Câu 20: Thông hiểu

    Tập xác định của hàm số y = \frac{\sqrt{9 - x^{2}}}{x^{2} - 6x + 8} là

    Ta có 9 − x2 ≥ 0 ⇔ (3−x)(3+x) ≥ 0 ⇔  − 3 ≤ x ≤ 3.

    Hàm số xác định khi và chỉ khi

    \left\{ \begin{matrix} 9 - x^{2} \geq 0 \\ x^{2} - 6x + 8 eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} - 3 \leq x \leq 3 \\ x eq 4 \\ x eq 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} - 3 \leq x \leq 3 \\ x eq 2 \\ \end{matrix} ight.. Vậy x ∈ [ − 3; 3] ∖ {2}.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 3 Hàm số bậc hai và đồ thị CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 45 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 3 Hàm số bậc hai và đồ thị CTST
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập