Lớp 10 Toán 10 - Cánh diều

Đề kiểm tra 15 phút Chương 3 Hàm số và đồ thị

Mô tả thêm: Đề kiểm tra 15 phút Toán 10 Hàm số và đồ thị gồm 20 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Cánh Diều.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Tập nghiệm của bất phương trình: 2x^{2}–7x–15≥0 là:

     Ta có: 2x^{2}–7x–15≥0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \le - \frac{3}{2}}\\{x \ge 5}\end{array}} ight..

    Vậy D=(-\infty ;-\frac{3}{2}]\cup [5;+\infty ).

  • Câu 2: Thông hiểu

    Xác định parabol (P): y = ax2 + bx + c, a ≠ 0 biết (P) cắt trục tung tại điểm có tung độ bằng 1 và có giá trị nhỏ nhất bằng \frac{3}{4} khi x = \frac{1}{2}.

    Ta có (P) cắt trục tung tại điểm có tung độ bằng 1: Khi x = 0 thì y = 1 ⇒ c = 1.

    (P)có giá trị nhỏ nhất bằng \frac{3}{4} khi x = \frac{1}{2} nên:

    \left\{ \begin{matrix} y\left( \frac{1}{2} ight) = \frac{3}{4} \\ \frac{- b}{2a} = \frac{1}{2} \\ \end{matrix} ight. ⇔ \left\{ \begin{matrix} \frac{1}{4}a + \frac{1}{2}b + 1 = \frac{3}{4} \\ \frac{- b}{2a} = \frac{1}{2} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \frac{1}{4}a + \frac{1}{2}b = - \frac{1}{4} \\ a + b = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} a = 1 \\ b = - 1 \\ \end{matrix} ight..

    Vậy (P): y = x2 − x + 1.

  • Câu 3: Thông hiểu

    Phương trình \left( x^{2} + 5x + 4 ight)\sqrt{x + 3} =0 có bao nhiêu nghiệm?

    Điều kiện xác định của phương trình là x ≥  − 3.

    Phương trình tương đương với \Leftrightarrow \left\{ \begin{matrix}x \geq - 3 \\\left\lbrack \begin{matrix}x = - 1 \\x = - 4 \\x = - 3 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}x = - 1 \\x = - 3 \\\end{matrix} ight..

    Vậy phương trình có hai nghiệm.

  • Câu 4: Vận dụng cao

    Tổng các nghiệm của phương trình \sqrt{4x^{2} - 1} - \sqrt{2x + 1} = 1 + x - 2x^{2} là:

    Đặt \sqrt{4x^{2} - 1} = a;\sqrt{2x + 1} = b(a,b \geq 0).

    Ta có 1 + x - 2x^{2} = - \frac{1}{2}(4x^{2} - 1) + \frac{1}{2}(2x + 1).

    Phương trình trở thành a - b = \frac{1}{2}\left( b^{2} - a^{2} ight) \Leftrightarrow a = b

    Thay vào ta được x = 1;x = - \frac{1}{2}. Vậy tổng các nghiệm của phương trình là \frac{1}{2}.

  • Câu 5: Nhận biết

    Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol có trục đối xứng x =  − 3.

    Vì (P) có trục đối xứng x =  − 3 nên - \frac{b}{2a} = - 3 \Leftrightarrow - \frac{3}{2a} = - 3 \Leftrightarrow a = \frac{1}{2}.

    Vậy (P):y = \frac{1}{2}x^{2} + 3x - 2.

  • Câu 6: Thông hiểu

    Tập nghiệm của bất phương trình x(x + 5) \leqslant 2({x^2} + 2) là:

    Ta có:

    \begin{matrix} x(x + 5) \leqslant 2({x^2} + 2) \hfill \\ \Leftrightarrow {x^2} + 5x \leqslant 2{x^2} + 4 \hfill \\ \Leftrightarrow - {x^2} + 5x - 4 \leqslant 0 \hfill \\ \Leftrightarrow x \in \left( { - \infty ;1} ight] \cup \left[ {4; + \infty } ight) \hfill \\ \end{matrix}

  • Câu 7: Nhận biết

    Tam thức bậc hai f(x) = 4x2 − 12x + 9 nhận giá trị âm khi và chỉ khi

    Chọn Ta có: f(x) = 4x^{2} - 12x + 9 = 0 \Leftrightarrow x = \frac{3}{2}

    Dựa vào bảng xét dấu thì ta thấy không có giá trị x nào để f(x) < 0.

  • Câu 8: Nhận biết

    Số nghiệm của phương trình \sqrt{8-x^{2}}=\sqrt{x+2} là

    Điều kiện: \left\{ {\begin{array}{*{20}{c}} {8 - {x^2} \geqslant 0} \\ {x + 2 \geqslant 0} \end{array}} ight.

    Phương trình tương đương:

    \begin{gathered} \sqrt {8 - {x^2}} = \sqrt {x + 2} \hfill \\ \Leftrightarrow 8 - {x^2} = x + 2 \hfill \\ \Leftrightarrow - {x^2} - x + 6 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 2} \\ {x = - 3} \end{array}} ight. \hfill \\ \end{gathered}

    Kết hợp điều kiện ta được: x=2 thỏa mãn điều kiện

    Vậy phương trình đã cho có một nghiệm.

  • Câu 9: Nhận biết

    Cho hàm số có đồ thị như hình bên dưới.

    Khẳng định nào sau đây là đúng?

    Trên khoảng (0;2) đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.

  • Câu 10: Thông hiểu

    Tìm m để hàm số y = (2m−1)x + 7 đồng biến trên ℝ.

    Hàm số y = (2m−1)x + 7 đồng biến trên ℝ khi 2m − 1 > 0 hay m > \frac{1}{2}.

  • Câu 11: Vận dụng

    Phương trình (x -1)(x + 3) + 2(x - 1)\sqrt{\frac{x + 3}{x - 1}} = 8 có mấy nghiệm ?

    Điều kiện: \left\lbrack \begin{matrix}x \leq - 3 \\x > 1 \\\end{matrix} ight.

    Đặt t = (x - 1)\sqrt{\frac{x + 3}{x - 1}}\Rightarrow t^{2} = (x - 1)(x + 3).

    PT đã cho trở thành:

    t^{2} + 2t - 8 = 0 \Leftrightarrow\left\lbrack \begin{matrix}t = 2\ \ \\t = - 4\ \ \ \\\end{matrix} ight.

    Với t = 2 ta được

    \begin{matrix}(x - 1)\sqrt{\frac{x + 3}{x - 1}} = 2 \\\Rightarrow (x - 1)(x + 3) = 4 \Leftrightarrow \left\lbrack\begin{matrix}x = - 1 + 2\sqrt{2}(TM) \\x = - 1 - 2\sqrt{2}(L) \\\end{matrix} ight.\ \\\end{matrix}

    Với t =  − 4 ta được ta được

    \begin{matrix}(x - 1)\sqrt{\frac{x + 3}{x - 1}} = - 4 \\\Rightarrow (x - 1)(x + 3) = 16 \Leftrightarrow \left\lbrack\begin{matrix}x = - 1 + 2\sqrt{5}(L) \\x = - 1 - 2\sqrt{5}(TM) \\\end{matrix} ight.\ \\\end{matrix}

    Vậy phương trình có hai nghiệm là x = - 1+ 2\sqrt{2} ; x = - 1 -2\sqrt{5}.

  • Câu 12: Nhận biết

    Tập xác định của hàm số y = \sqrt{8 - 2x} - x là:

    Điều kiện: 8 − 2x ≥ 0 ⇔ x ≤ 4. Vậy D = ( − ∞; 4].

  • Câu 13: Nhận biết

    Tam thức f(x) = x2 − 2x − 3 nhận giá trị dương khi và chỉ khi

    Ta có: f(x) = x^{2} - 2x - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, chọn đáp án x ∈ (−∞;−1) ∪ (3;+∞).

  • Câu 14: Thông hiểu

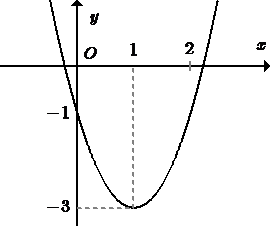
    Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

    Nhận xét:

    Parabol có bề lõm hướng lên.

    Parabol cắt trục hoành tại 2 điểm phân biệt có hoành độ âm. Xét các đáp án, đáp án y = 3x2 + 6x + 1 thỏa mãn.

  • Câu 15: Thông hiểu

    Tam thức bậc hai .

    Ta có .

    Bảng xét dấu

    Dựa vào bảng xét dấu .

  • Câu 16: Vận dụng

    Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?

    Nhìn vào đồ thị ta có:

    Bề lõm hướng xuống  ⇒ a < 0.

    Hoành độ đỉnh x = - \frac{b}{2a} > 0\Rightarrow \frac{b}{2a} < 0 \Rightarrow b > 0 .

    Đồ thị hàm số cắt trục tung tại điểm có tung độ âm  ⇒ c < 0.

    Do đó: a < 0, b > 0, c < 0.

  • Câu 17: Thông hiểu

    Tập nghiệm của phương trình: \sqrt{3-x+x^{2}}-\sqrt{2+x-x^{2}}=1 là:

    Điều kiện: \left\{ {\begin{array}{*{20}{c}} {3 - x + {x^2} \geqslant 0} \\ {2 + x - {x^2} \geqslant 0} \end{array}} ight. => x \in \left[ { - 1,2} ight]

    Phương trình tương đương

    \begin{matrix} \sqrt {3 - x + {x^2}} - \sqrt {2 + x - {x^2}} = 1 \hfill \\ \Leftrightarrow \sqrt {3 - x + {x^2}} - 2 + 1 - \sqrt {2 + x - {x^2}} = 0 \hfill \\ \Leftrightarrow \dfrac{{{x^2} - x - 1}}{{\sqrt {3 - x + {x^2}} + 2}} + \dfrac{{{x^2} - x - 1}}{{1 + \sqrt {2 + x - {x^2}} }} = 0 \hfill \\ \Leftrightarrow \left( {{x^2} - x - 1} ight)\left( {\dfrac{1}{{\sqrt {3 - x + {x^2}} + 2}} + \dfrac{1}{{1 + \sqrt {2 + x - {x^2}} }}} ight) = 0 \hfill \\ \end{matrix}

    Ta có: \frac{1}{{\sqrt {3 - x + {x^2}} + 2}} + \frac{1}{{1 + \sqrt {2 + x - {x^2}} }} > 0,\forall x \in \left[ { - 1,2} ight]

    \begin{matrix} \Leftrightarrow {x^2} - x - 1 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{{1 - \sqrt 5 }}{2}} \\ {x = \dfrac{{1 + \sqrt 5 }}{2}} \end{array}} ight.\left( {tm} ight) \hfill \\ \end{matrix}

    Vậy tập nghiệm của phương trình là: \left\{ {\frac{{1 + \sqrt 5 }}{2};\frac{{1 - \sqrt 5 }}{2}} ight\}

  • Câu 18: Nhận biết

    Xét tính đồng biến, nghịch biến của hàm số f(x) = x2 − 4x + 5 trên các khoảng (−∞; 2) và (2; +∞). Khẳng định nào sau đây đúng?

    Xét f(x) = x2 − 4x + 5.

    TXĐ: D = ℝ.

    Tọa độ đỉnh I(2; 1).

    Hàm số nghịch biến trên (−∞; 2), đồng biến trên (2; +∞).

  • Câu 19: Thông hiểu

    Cho hàm số y = (m + 2)x + \sqrt{2 - m}. Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên ℝ?

    Hàm số có dạng y = ax + b, nên để hàm số đồng biến trên ℝ khi và chỉ khi \left\{ \begin{matrix} m + 2 > 0 \\ 2 - m \geq 0 \\ \end{matrix} ight. \Leftrightarrow \left\{ \begin{matrix} m > - 2 \\ m \leq 2 \\ \end{matrix} ight.. Mặt khác do m ∈ ℤ nên m ∈ {−1;  0;  1;  2}. Vậy có 4 giá trị nguyên của m.

  • Câu 20: Nhận biết

    Cho tam thức bậc hai f(x) = {x^2} - 10x + 2. Kết luận nào sau đây đúng?

    Ta có:

    \begin{matrix}f\left( { - 2} ight) = {\left( { - 2} ight)^2} - 10.\left( { - 2} ight) + 2 = 26 > 0 \hfill \\ f\left( 1 ight) = {\left( 1 ight)^2} - 10.\left( 1 ight) + 2 = - 7 < 0 \hfill \\ \end{matrix}

    Vậy khẳng định đúng là f(–2) > 0.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 3 Hàm số và đồ thị Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 50 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 3 Hàm số và đồ thị
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập