Lớp 10 Toán 10 - Kết nối tri thức

Đề kiểm tra 15 phút Chương 3 Hệ thức lượng trong tam giác

Mô tả thêm: Đề kiểm tra 15 phút Toán 10 Hệ thức lượng trong tam giác gồm 20 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Kết nối tri thức.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \cos\alpha = \sqrt{1 - sin^{2}\alpha}.

    Ta có \cos\alpha = \sqrt{1 - sin^{2}\alpha} \Leftrightarrow \cos\alpha = \sqrt{cos^{2}\alpha} \Leftrightarrow \cos\alpha = \left| \cos\alpha ight| \Leftrightarrow \cos\alpha.

    Đẳng thức \left| \cos\alpha ight| \Leftrightarrow \cos\alpha\overset{}{ightarrow}\cos\alpha \geq 0\overset{}{ightarrow}điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc IV.

  • Câu 2: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha < 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 3: Nhận biết

    Cho \Delta ABC vuông tại B và có \widehat{C} = 25^{0}. Số đo của góc A là:

    Ta có: Trong \Delta ABC \widehat{A} + \widehat{B} + \widehat{C} = 180^{0} \Rightarrow \widehat{A} = 180^{0} - \widehat{B} - \widehat{C} = 180^{0} - 90^{0} - 25^{0} = 65^{0}.

  • Câu 4: Nhận biết

    Cho tam giác ABC có AB=1;AC=\sqrt2;\hat A=45^{\circ}. Tính độ dài cạnh BC.

     Áp dụng định lí côsin:

    BC^2=AB^2+AC^2-2.AB.AC.\cos A=1+2-2.1.\sqrt2.\cos45^{\circ} =1.

    Suy ra BC=1.

  • Câu 5: Vận dụng

    Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).

    Tính bán kinh của chiếc đĩa

    Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):

    Ta có: Bán kính của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.

    Nửa chu vi tam giác ABC: 

    \begin{matrix} p = \dfrac{{AB + AC + BC}}{2} \hfill \\ = \dfrac{{4,3 + 7,5 + 3,7}}{2} = \dfrac{{31}}{4}\left( {cm} ight) \hfill \\ \end{matrix}

    Áp dụng công thức Hê - rông tính diện tích tam giác ABC:

    \begin{matrix} S = \sqrt {p\left( {p - AB} ight)\left( {p - AC} ight)\left( {p - BC} ight)} \hfill \\ \Rightarrow S \approx 5,2\left( {c{m^2}} ight) \hfill \\ \end{matrix}

    Mặt khác 

    \begin{matrix} S = \dfrac{{AB.AC.BC}}{{4R}} \Rightarrow R = \dfrac{{AB.AC.BC}}{{4s}} \hfill \\ \Rightarrow R \approx 5,73\left( {cm} ight) \hfill \\ \end{matrix}

  • Câu 6: Vận dụng

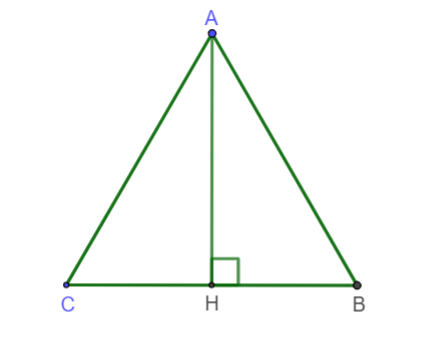
    Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30' (hình vẽ).

    Tính độ cao CH của ngọn núi

    Ngọn núi đó có độ cao CH so với mặt đất gần nhất với giá trị nào sau đây?

    Ta có: \widehat {ABC} = {90^0} + {15^0}30' = {105^0}30'

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat {ABC} + \widehat {CAB} + \widehat {ACB} = {180^0} \hfill \\ \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat {ABC} + \widehat {CAB}} ight) \hfill \\ \Rightarrow \widehat {ACB} = {180^0} - \left( {{{105}^0}30\prime + {{60}^0}} ight) \hfill \\ \Rightarrow \widehat {ACB} = {14^0}30\prime \hfill \\ \end{matrix}

    Áp dụng định lí sin cho tam giác ABC ta có:

    \begin{matrix} \dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{AC}}{{\sin \widehat {ABC}}} \hfill \\ \Rightarrow AC = \dfrac{{AB.\sin \widehat {ABC}}}{{\sin \widehat {ACB}}} \hfill \\ \Rightarrow AC = \dfrac{{70.\sin {{107}^0}30'}}{{\sin {{14}^0}30'}} \approx 269,4\left( m ight) \hfill \\ \end{matrix}

    Xét tam giác ACH vuông tại H ta có:

    \begin{matrix} CH = AC.\sin \widehat {CAH} \hfill \\ \Rightarrow CH \approx 269,4.\sin {30^0} \approx 134,7\left( m ight) \hfill \\ \end{matrix}

  • Câu 7: Nhận biết

    Cho \Delta ABCcó S = 84,a = 13,b = 14,c = 15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là:

    Ta có: S_{\Delta ABC} = \frac{a.b.c}{4R} \Leftrightarrow R = \frac{a.b.c}{4S} = \frac{13.14.15}{4.84} = \frac{65}{8}.

  • Câu 8: Thông hiểu

    Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230m. Góc giữa hai hàng rào MN và MP là 110^{\circ} (như hình vẽ)

    Diện tích mảnh đất mà gia đình bà Sáu sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?

    Diện tích mảnh đất của gia đình bà Sáu (tam giác MNP) là:

    S = \frac{1}{2}MN \cdot MP \cdot \sin M

    = \frac{1}{2} \cdot 150 \cdot 230 \cdot \sin110^{\circ} \approx 16209,7\left( {m}^{2}ight).

  • Câu 9: Nhận biết

    Tam giác ABC có BC = 10 và \widehat{A}=30°. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

     Ta có: \frac {BC}{\sin A}=2R \Leftrightarrow R= \frac{BC}{2\sin A} =\frac {10}{2.sin30^{\circ} }=10.

  • Câu 10: Thông hiểu

    Giá trị biểu thức S = {\cos ^2}{12^0} + {\cos ^2}{48^0} + {\cos ^2}{1^0} + {\cos ^2}{89^0} bằng:

    Ta có:

    \begin{matrix} S = {\cos ^2}{12^0} + {\cos ^2}{48^0} + {\cos ^2}{1^0} + {\cos ^2}{89^0} \hfill \\ = {\cos ^2}{12^0} + {\sin ^2}{12^0} + {\cos ^2}{1^0} + {\sin ^2}{1^0} \hfill \\ = 1 + 1 = 2 \hfill \\ \end{matrix}

  • Câu 11: Vận dụng

    Cho góc \alpha thỏa mãn \sin\alpha + \cos\alpha = \frac{5}{4}. Tính P = \sin\alpha.cos\alpha.

    Từ giả thiết, ta có \left( \sin\alpha + \cos\alpha ight)^{2} = \frac{25}{16} \Leftrightarrow 1 + 2sin\alpha.cos\alpha = \frac{25}{16}

    ightarrow P = \sin\alpha.cos\alpha = \frac{9}{32}.

  • Câu 12: Thông hiểu

    Cho góc \alpha thoả mãn 0^{\circ} < \alpha < 180^{\circ} và \cot\alpha = - 2. Giá trị của \sin\alpha là:

    Ta có: \cot\alpha = \frac{\cos\alpha}{\sin\alpha}

    \Rightarrow \cot^{2}\alpha = \frac{\cos^{2}\alpha}{\sin^{2}\alpha} = \frac{1 - \sin^{2}\alpha}{\sin^{2}\alpha}

    \Rightarrow 1 + \cot^{2}\alpha = \frac{1}{\sin^{2}\alpha}.

    Do đó \sin^{2}\alpha = \frac{1}{1 + \cot^{2}\alpha} = \frac{1}{1 + ( - 2)^{2}} = \frac{1}{5}.

    Vì 0^{0} < \alpha < 180^{\circ} nên \sin\alpha =\frac{\sqrt{5}}{5}.

  • Câu 13: Nhận biết

    Cho \Delta ABC có a = 4,c = 5,B = 150^{0}. Diện tích của tam giác là:

    Ta có: S_{\Delta ABC} = \frac{1}{2}a.c.sinB = \frac{1}{2}.4.5.sin150^{0} = 5.

  • Câu 14: Vận dụng

    Cho \pi < \alpha < \frac{3\pi}{2}. Xác định dấu của biểu thức M = \sin\left( \frac{\pi}{2} - \alpha ight).cot(\pi + \alpha).

    Ta có:

    \left\{ \begin{matrix} \pi < \alpha < \frac{3\pi}{2} ightarrow - \frac{3\pi}{2} < - \alpha < - \pi \\ \pi < \alpha < \frac{3\pi}{2} ightarrow 2\pi < \pi + \alpha < \frac{5\pi}{2} \\ \end{matrix} ight. ightarrow - \pi < \frac{\pi}{2} - \alpha < - \frac{\pi}{2} và \overset{}{ightarrow}\cot(\pi + \alpha) > 0

    \overset{}{ightarrow}\sin\left( \frac{\pi}{2} - \alpha ight) < 0

    \overset{}{ightarrow}M < 0.

  • Câu 15: Thông hiểu

    Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và \widehat{ACB} = 60{^\circ}. Tính độ dài cạnh cạnh BC.

    Gọi M,\ \ N lần lượt là trung điểm của AB,\ \ BC.

    \overset{}{ightarrow}MN là đường trung bình của \Delta ABC.

    \overset{}{ightarrow}MN = \frac{1}{2}AC. Mà MN = 3, suy ra AC = 6.

    Theo định lí hàm cosin, ta có:

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{ACB}

    \Leftrightarrow 9^{2} = 6^{2} + BC^{2} - 2.6.BC.cos60{^\circ}

    \Rightarrow BC = 3 + 3\sqrt{6}

  • Câu 16: Nhận biết

    Tam giác ABC có AB = 2,\ \ AC = 1 và \widehat{A} = 60{^\circ}. Tính độ dài cạnh BC.

    Theo định lí hàm cosin, ta có BC^{2} = AB^{2} + AC^{2} - 2AB.AC.cos\widehat{A} = 2^{2} + 1^{2} - 2.2.1.cos60{^\circ} = 3 \Rightarrow BC = \sqrt{3}.

  • Câu 17: Thông hiểu

    Diện tích tam giác có ba cạnh lần lượt là \sqrt{3},\sqrt{2} và 1 là:

    Nửa chu vi của tam giác là: p = \frac{{a + b + c}}{2} = \frac{{\sqrt 3 + \sqrt 2 + 1}}{2}

    Áp dụng công thức Herong ta có:

    \begin{matrix} S = \sqrt {p\left( {p - a} ight)\left( {p - b} ight)\left( {p - a} ight)} \hfill \\ S = \sqrt {p\left( {p - \sqrt 3 } ight)\left( {p - \sqrt 2 } ight)\left( {p - 1} ight)} \hfill \\ S = \dfrac{{\sqrt 2 }}{2} \hfill \\ \end{matrix}

  • Câu 18: Thông hiểu

    Cho tam giác ABC có b = 7; c = 5, \cos A = \frac{3}{5}. Đường cao h_{a} của tam giác ABC là:

    Ta có: a^{2} = b^{2} + c^{2} - 2bc\cos A = 7^{2} + 5^{2} - 2.7.5.\frac{3}{5} = 32 \Rightarrow a = 4\sqrt{2}.

    Mặt khác: sin^{2}A + cos^{2}A = 1 \Rightarrow sin^{2}A = 1 - cos^{2}A = 1 - \frac{9}{25} = \frac{16}{25} \Rightarrow \sin A = \frac{4}{5} (Vì \sin A > 0).

    Mà: S_{\Delta ABC} = \frac{1}{2}b.c.sinA = \frac{1}{2}a.h_{a} \Rightarrow h_{a} = \frac{bc\sin A}{a} = \frac{7.5.\frac{4}{5}}{4\sqrt{2}} = \frac{7\sqrt{2}}{2}.

  • Câu 19: Nhận biết

    Giá trị cot\frac{\pi }{6} là:

     Ta có: cot\frac{\pi }{6} =\sqrt3.

  • Câu 20: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sin\alpha,\ cos\alpha cùng dấu?

    Điểm cuối của \alpha thuộc góc phần tư thứ nhất thì \sin\alpha > 0, \cos\alpha > 0.

    Điểm cuối của \alpha thuộc góc phần tư thứ nhất thì \sin\alpha < 0, \cos\alpha < 0.

    Vậy nếu \sin\alpha,\ cos\alpha cùng dấu thì điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc III.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 3 Hệ thức lượng trong tam giác Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 27 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 3 Hệ thức lượng trong tam giác
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập