Lớp 12 Toán 12

Đề kiểm tra 15 phút Chương 3 Nguyên hàm - Tích phân và ứng dụng

Mô tả thêm: Bài kiểm tra 15 phút Nguyên hàm - Tích phân và ứng dụng của chúng tôi gồm 4 mức độ được thay đổi ngẫu nhiên, giúp bạn đọc rèn luyện củng cố kiến thức tốt hơn.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Nguyên hàm của hàm số f\left( x ight) = {2^x} + {e^x} là:

     Ta có: \int {\left( {{2^x} + {e^x}} ight)dx} = \int {{2^x}dx} + \int {{e^x}dx} = \frac{{{2^x}}}{{\ln 2}} + {e^x} + C

  • Câu 2: Thông hiểu

    Cho hình phẳng (H) giới hạn bởi đường parabol (P):y = x^{2} - x + 2 và tiếp tuyến của đồ thị hàm số y = x^{2} + 1 tại điểm có tọa độ (1;2). Diện tích của hình (H) là:

    Xét hàm số y = x^{2} + 1 trên \mathbb{R}. Ta có: y' = 2x

    Khi đó phương trình tiếp tuyến tại điểm (1;2) của đồ thị hàm số y = x^{2} + 1 là

    y = y'(1)(x - 1) + 2 \Leftrightarrow y = 2x

    Gọi ∆ là đường thẳng có phương trình y = 2x. Xét phương trình tương giao của (P) và ∆

    x^{2} - x + 2 = 2x \Leftrightarrow x^{2} - 3x + 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 2 \\ \end{matrix} ight.

    Gọi S là diện tích hình phẳng (H) khi đó

    S = \int_{1}^{2}{\left| \left( x^{2} - x + 2 ight) - 2x ight|dx} = \int_{1}^{2}{\left| x^{2} - 3x + 2 ight|dx}

    Vì x^{2} - 3x + 2 \leq 0;\forall x \in \lbrack 1;2bracknên

    S = - \int_{1}^{2}{\left( x^{2} - 3x + 2 ight)dx}

    = - \left. \ \left( \frac{x^{3}}{3} - \frac{3x^{2}}{2} + 2x ight) ight|_{1}^{2} = - \left( \frac{2}{3} - \frac{5}{6} ight) = \frac{1}{6}

  • Câu 3: Vận dụng

    Tính thể tích của một vật thể nằm giữa hai mặt phẳng x = 0;x = \pi, biết thiết diện của vật thể cắt bởi mặt phẳng \left( P ight) vuông góc với trục Ox tại điểm có hoành độ  là một tam giác đều có cạnh bằng 2\sqrt {\sin x}

     Diện tích thiết diện là S\left( x ight) = \frac{{{{\left( {2\sqrt {\sin x} } ight)}^2}.\sqrt 3 }}{4} = \sqrt 3 \sin x

    Ta có thể tích cần tính là V = \int\limits_0^\pi {\sqrt 3 \sin xdx = \left. { - \sqrt 3 \cos x} ight|_0^\pi = } 2\sqrt 3

  • Câu 4: Nhận biết

    Họ nguyên hàm của hàm số f(x) = \frac{1}{x} + \sin x là:

    Ta có: \int_{}^{}{f(x)dx} = \int_{}^{}{\left( \frac{1}{x} + \sin x ight)dx} = \ln|x| - \cos x + C.

  • Câu 5: Thông hiểu

    Tính diện tích S_{D} của hình phẳng D được giới hạn bởi các đường y = \left| \frac{\ln x}{x} ight|, trục hoành và các đường thẳng x = \frac{1}{e};x = 2?

    Diện tích hình phẳng cần tìm là:

    S_{D} = \int_{\frac{1}{e}}^{2}{\left| \frac{\ln x}{x} ight|dx} = \int_{\frac{1}{e}}^{1}{\left| \frac{\ln x}{x} ight|dx} + \int_{1}^{2}{\left| \frac{\ln x}{x} ight|dx}

    = - \int_{\frac{1}{e}}^{1}{\frac{\ln x}{x}dx} + \int_{1}^{2}{\frac{\ln x}{x}dx}

    = - \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{\frac{1}{e}}^{1} + \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{1}^{2}

    = \frac{1}{2} + \frac{\ln^{2}2}{2} =\frac{1}{2}\left( 1 + \ln^{2}2 ight)

  • Câu 6: Thông hiểu

    Cho hàm số y = \cos4x có một nguyên hàm là F(x); F\left( \frac{\pi}{4} ight) = 2. Khẳng định nào sau đây đúng?

    Ta có: F(x) = \int_{}^{}{\cos4x}dx =\frac{1}{4}\sin4x + C

    F\left( \frac{\pi}{4} ight) = 2 \Rightarrow C = 2

    Ta được F(x) = \frac{1}{4}\sin4x +2

    \Rightarrow \int_{}^{}{F(x)dx} =\int_{}^{}{\left( \frac{1}{4}\sin4x + 2 ight)dx}

    = - \frac{\cos4x}{16} + 2x +C

  • Câu 7: Thông hiểu

    Gọi F(x) là một nguyên hàm của hàm số f\left( x ight) = {\left( {2x - 3} ight)^2} thỏa mãn F\left( 0 ight) = \frac{1}{3}. Tính giá trị của biểu thức A = {\log _2}\left[ {3F\left( 1 ight) - 2F\left( 2 ight)} ight]

     F\left( x ight) = \int {{{\left( {2x - 3} ight)}^2}dx = \frac{1}{2}\int {{{\left( {2x - 3} ight)}^2}d\left( {2x - 3} ight) = } \frac{1}{2}.\frac{{{{\left( {2x - 3} ight)}^2}}}{3} + C}

    Ta có: F\left( 0 ight) = \frac{1}{3} \Rightarrow C = \frac{{29}}{6}

    F\left( 1 ight) = \frac{1}{2}.\left( {\frac{{ - 1}}{3}} ight) + \frac{{29}}{6} = \frac{{14}}{3};F\left( 2 ight) = \frac{1}{2}.\left( {\frac{1}{3}} ight) + \frac{{29}}{6} = 5

    => A = {\log _2}\left[ {3F\left( 1 ight) - 2F\left( 2 ight)} ight] = A = {\log _2}\left[ {3\frac{{14}}{3} - 2.5} ight] = {\log _2}4 = 2

  • Câu 8: Thông hiểu

    Tìm một nguyên hàm của hàm số f\left( x ight) = \frac{{\ln x}}{x}.\sqrt {{{\ln }^2}x + 1}?

    Ta có: F(x) = \int_{}^{}{\frac{\ln x}{x}\sqrt{\ln^{2}x + 1}dx}

    Đặt \sqrt{ln^{2}x + 1} \Rightarrow t^{2}= \ln^{2}x + 1 \Rightarrow tdt = \frac{\ln x}{x}dx

    Khi đó F(x) = \int_{}^{}{t^{2}dt} =\frac{t^{3}}{3} + C = \frac{\sqrt{\left( \ln^{2}x + 1 ight)^{3}}}{3} +C.

  • Câu 9: Thông hiểu

    Giả sử \int_{}^{}\frac{(2x + 3)dx}{x(x + 1)(x + 2)(x + 3) + 1} = - \frac{1}{g(x)} + C với C là hằng số. Tổng các nghiệm của phương trình g(x) = 0 bằng:

    Ta có: \int_{}^{}\frac{(2x + 3)dx}{x(x + 1)(x + 2)(x + 3) + 1} = \int_{}^{}\frac{(2x + 3)dx}{\left( x^{2} + 3x + 2 ight)\left( x^{2} + 3x ight) + 1}

    Đặt t = x^{2} + 3x \Rightarrow dt = (2x + 3)dx

    \int_{}^{}\frac{dt}{(t + 2)t + 1} = \int_{}^{}\frac{dt}{(t + 1)^{2}} = - \frac{1}{t + 1} + C = - \frac{1}{x^{2} + 3x + 1} + C

    \Rightarrow g(x) = x^{2} + 3x + 1

    Theo định lí Vi – et ta thấy phương trình g(x) = 0 có hai nghiệm x_{1};x_{2} và x_{1} + x_{2} = - 3.

  • Câu 10: Vận dụng

    Cho hàm số F(x) là một nguyên hàm của hàm số f(x) = \frac{2\cos x -1}{\sin^{2}x} trên khoảng (0;\pi). Biết rằng giá trị lớn nhất của F(x) trên khoảng (0;\pi) là \sqrt{3}. Chọn mệnh đề đúng trong các mệnh đề sau?

    Ta có: \int_{}^{}{f(x)dx} =\int_{}^{}{\dfrac{2\cos x - 1}{\sin^{2}x}dx} =\int_{}^{}{\dfrac{2\cos x}{\sin^{2}x}dx} -\int_{}^{}{\dfrac{1}{\sin^{2}x}dx}

    = \int_{}^{}\frac{2d\left( \sin xight)}{\sin^{2}x} - \int_{}^{}{\frac{1}{\sin^{2}x}dx} = - \frac{2}{\sin x} + \cot x + C

    Vì F(x) là một nguyên hàm của hàm số f(x) = \frac{2\cos x -1}{\sin^{2}x} trên khoảng (0;\pi) nên hàm số F(x) có công thức dạng F(x) = - \frac{2}{\sin x} + \cot x + C với mọi x \in (0;\pi)

    Xét hàm số F(x) = - \frac{2}{\sin x} + \cot x + C xác định và liên tục trên (0;\pi)

    Ta có: F'(x) = f(x) = \frac{2\cos x -1}{\sin^{2}x}

    \Rightarrow F'(x) = 0\Leftrightarrow \frac{2\cos x - 1}{\sin^{2}x} = 0

    \Leftrightarrow \cos x = \frac{1}{2} \Leftrightarrow x = \pm \frac{\pi}{3} + k2\pi;\left( k\mathbb{\in Z} ight)

    Trên khoảng (0;\pi) phương trình F'(x) = 0 có một nghiệm x = \frac{\pi}{3}

    Ta có bảng biến thiên như sau:

    \underset{(0;\pi)}{\max F(x)} = F\left( \frac{\pi}{3} ight) = - \sqrt{3} + C. Theo bài ra ta có: - \sqrt{3} + C = \sqrt{3} \Rightarrow C = 2\sqrt{3}

    Do đó F(x) = - \frac{2}{\sin x} + \cot x + 2\sqrt{3} suy ra F\left( \frac{\pi}{6} ight) = 3\sqrt{3} - 4.

  • Câu 11: Thông hiểu

    Cho hàm số y = f(x) liên tục trên đoạn \lbrack 0;10brack và \int_{0}^{10}{f(x)dx} = 7 và \int_{2}^{6}{f(x)dx} = 3. Tính F = \int_{0}^{2}{f(x)dx} + \int_{6}^{10}{f(x)dx}?

    Ta có: \int_{0}^{10}{f(x)dx} = \int_{0}^{2}{f(x)dx} + \int_{2}^{6}{f(x)dx} + \int_{6}^{10}{f(x)dx}

    \Rightarrow F = \int_{0}^{2}{f(x)dx} + \int_{6}^{10}{f(x)dx} = \int_{0}^{10}{f(x)dx} - \int_{2}^{6}{f(x)dx} = 7 - 3 = 4

  • Câu 12: Nhận biết

    Hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn \lbrack 1;3brack, trục Ox và hai đường thẳng x = 1;x = 3 có diện tích là:

    Công thức tính diện tích cần tìm là: S = \int_{1}^{3}{\left| f(x) ight|dx}.

  • Câu 13: Nhận biết

    Cho các hàm số f(x) và F(x) liên tục trên \mathbb{R} thỏa mãn F'(x) = f(x) với \forall x\mathbb{\in R}. Tính I = \int_{0}^{1}{f(x)dx}, biết rằng F(0) = 2;F(1) = 5?

    Ta có: I = \int_{0}^{1}{f(x)dx} = F(1) - F(0) = 3.

  • Câu 14: Vận dụng cao

    Trong hệ trục tọa độ Oxy, cho parabol \left( P ight):y = {x^2} và hai đường thẳng y = a;y = b;\left( {0 < a < b} ight) (mô tả như hình vẽ). Gọi {S_1} là diện tích hình phẳng giới hạn bới và đường thẳng y=a (phần tô màu đen); S_2 là diện tích hình phẳng giới hạn bới parabol \left( P ight) và đường thẳng y=b (phần gạch chéo). Với điều kiện nào sau đây của a,b thì {S_1} = 2{S_2}?

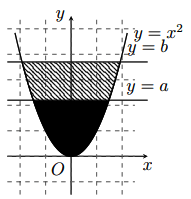
    Tìm điều kiện của a và b

    Phương trình hoành độ giao điểm của \left( P ight) và đường thẳng y=b là:

    {x^2} = b \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = \sqrt b } \\ {x = - \sqrt b } \end{array}} ight.

    Phương trình hoành độ giao điểm của \left( P ight) và đường thẳng y=a là:

    {x^2} = a \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = \sqrt a } \\ {x = - \sqrt a } \end{array}} ight.

    Diện tích hình phẳng giới hạn bởi \left( P ight) và y=b là:

    \begin{matrix} S = 2\int\limits_0^{\sqrt b } {{{\left( {b - x} ight)}^2}dx} = \left. {2\left( {bx - \dfrac{{{x^3}}}{3}} ight)} ight|_0^{\sqrt b } \hfill \\ = 2\left( {b\sqrt b - \dfrac{{b\sqrt b }}{3}} ight) = \dfrac{{4b\sqrt b }}{3} \hfill \\ \end{matrix}

    Diện tích hình phẳng giới hạn bởi \left( P ight) và y=a là:

    \begin{matrix} S = 2\int\limits_0^{\sqrt a } {{{\left( {a - x} ight)}^2}dx} = \left. {2\left( {ax - \dfrac{{{x^3}}}{3}} ight)} ight|_0^{\sqrt a } \hfill \\ = 2\left( {a\sqrt a - \dfrac{{a\sqrt a }}{3}} ight) = \dfrac{{4a\sqrt a }}{3} \hfill \\ \end{matrix}

    Khi đó: {S_1} = 2{S_2} \Leftrightarrow \frac{{4b\sqrt b }}{3} = 2\frac{{4a\sqrt a }}{3} \Rightarrow b = \sqrt[3]{4}a

     

  • Câu 15: Thông hiểu

    Trong hệ trục tọa độ Oxy cho elip (E) có phương trình \frac{x^{2}}{25} + \frac{y^{2}}{9} = 1. Hình phẳng (H) giới hạn bởi nửa elip nằm trên trục hoành và trục hoành. Quay hình (H) xung quanh trục Ox ta được khối tròn xoay, tính thể tích khối tròn xoay đó?

    Ta có: \frac{y^{2}}{9} = 1 - \frac{x^{2}}{25} \Rightarrow y = \sqrt{9\left( 1 - \frac{x^{2}}{25} ight)} với x \in \lbrack - 5;5brack

    Khi đó thể tích cần tìm là: V = \pi\int_{- 5}^{5}{\left( 9 - \frac{9x^{2}}{25} ight)dx} = 60\pi

  • Câu 16: Nhận biết

    Nguyên hàm của hàm số f(x) = \frac{1}{x\sqrt{x}} là:

    Ta có: \int_{}^{}{f(x)dx} = \int_{}^{}{\frac{1}{x\sqrt{x}}dx}

    = \int_{}^{}{x^{- \frac{3}{2}}dx=}\dfrac{x^{- \frac{1}{2}}}{- \dfrac{1}{2}} + C = - \frac{2}{\sqrt{x}} +C.

  • Câu 17: Nhận biết

    Tích phân I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} ight)dx} có giá trị là:

     Tích phân I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} ight)dx} có giá trị là:

    I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} ight)dx} = \left. {\left( { - \frac{1}{x} + {x^2}} ight)} ight|_1^2 = \frac{7}{2}

    Ngoài ra ta có thể sử dụng máy tính cầm tay nhập trực tiếp biểu thức và tính ra kết quả.

  • Câu 18: Vận dụng

    Cho hàm số f(x) xác định trên \mathbb{R}\backslash \left\{ 1 ight\} thỏa mãn f'\left( x ight) = \frac{2}{{x - 1}};f\left( 0 ight) = 3;f\left( 2 ight) = 4. Tính giá trị của biểu thức  N = f\left( { - 2} ight) + f\left( 5 ight)

     

    f\left( x ight) = \int {f'\left( x ight)dx} = \int {\frac{2}{{x - 1}}dx} = \ln \left| {2x - 1} ight| + C

    => f\left( x ight) = \left\{ {\begin{array}{*{20}{c}} {2\ln \left( {x - 1} ight) + {C_1}{\text{ khi x > }}1} \\ {2\ln \left| {1 - x} ight| + {C_2}{\text{ khi x < }}1} \end{array}} ight.

    Theo bài ra ta có: \left\{ {\begin{array}{*{20}{c}} {f\left( 0 ight) = 3 \Rightarrow \ln \left( {1 - 0} ight) + {C_2} = 3} \\ {f\left( 2 ight) = 4 \Rightarrow \ln \left( {2 - 1} ight) + {C_1} = 4} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{C_2} = 3} \\ {{C_1} = 4} \end{array}} ight.

    => f\left( x ight) = \left\{ {\begin{array}{*{20}{c}} {2\ln \left( {x - 1} ight) + 4{\text{ khi x > }}1} \\ {2\ln \left| {1 - x} ight| + 3{\text{ khi x < }}1} \end{array}} ight.

    => N = f\left( { - 2} ight) + f\left( 5 ight) = \left\{ {2\ln \left[ {1 - \left( { - 2} ight)} ight] + 3} ight\} + \left\{ {2\ln \left( {5 - 1} ight) + 4} ight\}

    = 2\ln 3 + 2\ln 4 + 7

  • Câu 19: Vận dụng cao

    Biết luôn có hai số a;b để F(x) = \frac{ax + b}{x + 4};(4a - b eq 0) là một nguyên hàm của hàm số f(x) và thỏa mãn 2f^{2}(x) = \left\lbrack F(x) - 1 ightbrack.f'(x). Khẳng định nào sau đây là đúng và đầy đủ nhất?

    Do 4a - b eq 0 \Rightarrow F(x) eq C;\forall x\mathbb{\in R}. Vì luôn có hai số a;b để F(x) = \frac{ax + b}{x + 4};(4a - b eq 0) là một nguyên hàm của hàm số f(x) nên f(x) không phải là hàm hằng.

    Từ giả thiết 2f^{2}(x) = \left\lbrack F(x) - 1 ightbrack.f'(x) \Leftrightarrow \frac{2f(x)}{F(x) - 1} = \frac{f'(x)}{f(x)}

    Lấy nguyên hàm hai vế với vi phân dx ta được:

    \int_{}^{}{\frac{2f(x)}{F(x) - 1}dx} =\int_{}^{}{\frac{f'(x)}{f(x)}dx}\Leftrightarrow 2\ln\left| F(x) - 1ight| = \ln\left| f(x) ight| + C với C là hằng số.

    \Leftrightarrow 2ln\left| F(x) - 1 ight| + \ln e^{C} = \ln\left| f(x) ight|

    \Leftrightarrow \left| f(x) ight| = e^{C}.\left\lbrack F(x) - 1 ightbrack^{2} = e^{C}.\left( \frac{(a - 1)x + b - 4}{x + 4} ight)

    \Leftrightarrow \left\lbrack\begin{matrix}f(x) = e^{C}.\left\lbrack \dfrac{(a - 1)x + b - 4}{x + 4}ightbrack^{2} \\f(x) = - e^{C}.\left\lbrack \dfrac{(a - 1)x + b - 4}{x + 4}ightbrack^{2} \\\end{matrix} ight.

    TH1: f(x) = e^{C}.\left\lbrack \frac{(a - 1)x + b - 4}{x + 4} ightbrack^{2} ta có: F'(x) = f(x) \Rightarrow f(x) = \frac{4a - b}{(x + 4)^{2}}

    Đồng nhất hệ số ta có:

    e^{C}.\left\lbrack (a - 1)x + b - 4 ightbrack^{2} = 4a - b;\forall x\mathbb{\in R}

    \Leftrightarrow \left\{ \begin{matrix}a = 1 \\e^{C}.(b - 4)^{2} = 4 - b \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}a = 1 \\\left\lbrack \begin{matrix}b = 4 \\b = \dfrac{4e^{C} - 1}{e^{C}} \\\end{matrix} ight.\ \\\end{matrix} ight.

    Loại b = 4 do điều kiện 4a - b eq 0. Do đó (a;b) = \left( 1;\frac{4e^{C} - 1}{e^{C}} ight)

    TH2: f(x) = - e^{C}.\left\lbrack \frac{(a - 1)x + b - 4}{x + 4} ightbrack^{2} ta có: F'(x) = f(x) \Rightarrow f(x) = \frac{4a - b}{(x + 4)^{2}}

    Đồng nhất hệ số ta có:

    - e^{C}.\left\lbrack (a - 1)x + b - 4 ightbrack^{2} = 4a - b;\forall x\mathbb{\in R}

    \Leftrightarrow \left\{ \begin{matrix}a = 1 \\- e^{C}.(b - 4)^{2} = 4 - b \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}a = 1 \\\left\lbrack \begin{matrix}b = 4 \\b = \dfrac{4e^{C} + 1}{e^{C}} \\\end{matrix} ight.\ \\\end{matrix} ight.

    Loại b = 4 do điều kiện 4a - b eq 0. Do đó (a;b) = \left( 1;\frac{4e^{C} + 1}{e^{C}} ight)

    Vậy khẳng định đúng và đầy đủ nhất là a = 1;b\mathbb{= R}\backslash\left\{ 4 ight\}.

  • Câu 20: Vận dụng

    Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):(x - 3)^{2} + (y - 1)^{2} =1.

    Tính thể tích của khối tròn xoay thu được khi quay hình phẳng giới hạn bởi đường tròn (C) quanh trục hoành.

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):(x - 3)^{2} + (y - 1)^{2} =1.

    Tính thể tích của khối tròn xoay thu được khi quay hình phẳng giới hạn bởi đường tròn (C) quanh trục hoành.

    Chỗ nhập nội dung câu trả lời tự luận
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 3 Nguyên hàm - Tích phân và ứng dụng Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 16 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 3 Nguyên hàm - Tích phân và ứng dụng
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập