Lớp 12 Toán 12 - Chân trời sáng tạo

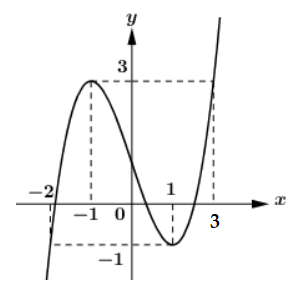
Đề kiểm tra 15 phút Chương 4 Nguyên hàm Tích phân CTST

Mô tả thêm: Bài kiểm tra 15 phút Nguyên hàm Tích phân của chúng tôi gồm 4 mức độ được thay đổi ngẫu nhiên, giúp bạn đọc rèn luyện củng cố kiến thức tốt hơn.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng cao

    Cho hình phẳng (H) giới hạn bởi các đường y = \left| x^{2} - 1 ight| và y = k, với 0 < k < 1. Tìm k để diện tích hình phẳng (H) gấp hai lần diện tích hình phẳng được kẻ sọc ở hình vẽ bên (Kết quả được làm tròn đến hàng phần trăm)

    Đáp án: 0,59

    Đáp án là:

    Cho hình phẳng (H) giới hạn bởi các đường y = \left| x^{2} - 1 ight| và y = k, với 0 < k < 1. Tìm k để diện tích hình phẳng (H) gấp hai lần diện tích hình phẳng được kẻ sọc ở hình vẽ bên (Kết quả được làm tròn đến hàng phần trăm)

    Đáp án: 0,59

    Gọi S là diện tích hình phẳng (H). Lúc dó S = 2S_{1} + 2S_{2}, trong đó S_{1} là diện tích phần gạch sọc ở bên phải Oy và S_{2} là diện tích phần gạch ca rô trong hình vẽ bên.

    GọiA,B là các giao diếm có hoành độ dương của đường thẳng y = k và đồ thị hàm sốy = \left| x^{2} - 1 ight|, trong đó A\left( \sqrt{1 - k};k ight) và B\left( \sqrt{1 + k};k ight).

    Thco yêu cầu bài toán S = 2 \cdot 2S_{1} \Leftrightarrow S_{1} = S_{2}.

    \Leftrightarrow \int_{0}^{\sqrt{1 - k}}{\left( 1 - x^{2} - k ight)dx}\ = \int_{\sqrt{1 - k}}^{1}{\left( k - 1 + x^{2} ight)dx} + \int_{1}^{\sqrt{1 + k}}{\left( k - x^{2} + 1 ight)dx}.

    \Leftrightarrow \ (1 - k)\sqrt{1 - k} - \frac{1}{3}(1 - k)\sqrt{1 - k}

    = \frac{1}{3} - (1 - k) - \frac{1}{3}(1 - k)\sqrt{1 - k} + (1 - k)\sqrt{1 - k}

    \ + (1 + k)\sqrt{1 + k} - \frac{1}{3}(1 + k)\sqrt{1 + k} - (1 + k) + \frac{1}{3}

    \Leftrightarrow \ \frac{2}{3}(1 + k)\sqrt{1 + k} = \frac{4}{3}

    \Leftrightarrow \left( \sqrt{1 + k} ight)^{3} = 2 \Leftrightarrow k = \sqrt[3]{4} - 1 \approx 0,59.

  • Câu 2: Nhận biết

    Tìm nguyên hàm của hàm số f(x) = (x + 1)(x + 2)(x + 3)?

    Ta có:

    f(x) = (x + 1)(x + 2)(x + 3) = x^{3} + 6x^{2} + 11x + 6

    \Rightarrow F(x) = \frac{x^{4}}{4} + 2x^{3} + \frac{11}{2}x^{2} + 6x + C

  • Câu 3: Nhận biết

    Cho hình vẽ:

    Diện tích hình phẳng bôi đậm trong hình vẽ được xác định theo công thức:

    Dựa vào đồ thị hàm số ta thấy công thức tính diện tích hình phẳng cần tìm là:

    S = \int_{- 1}^{2}{\left( - x^{2} + 3 - x^{2} + 2x + 1 ight)dx} = \int_{- 1}^{2}{\left( - 2x^{2} + 2x + 4 ight)dx}.

  • Câu 4: Nhận biết

    Cho hàm số f(x) biết f(0) = 1, f'(x) liên tục trên \lbrack 0;3brack và \int_{0}^{3}{f'(x)dx} = 9. Tính f(3)?

    Ta có:

    \int_{0}^{3}{f'(x)dx} = 9 \Leftrightarrow \left. \ f(x) ight|_{0}^{3} = 9 \Rightarrow f(3) - f(0) = 9

    \Rightarrow f(3) = 9 + f(0) = 9 + 1 = 10

  • Câu 5: Vận dụng cao

    Gọi F(x) là một nguyên hàm của hàm số f\left( x ight) = \frac{1}{{{x^2}\left( {x + 1} ight)}}, F(x) thỏa mãn F(X) + F(-2) = 0,5. Tính F(2) + F(-3)

     Ta có: f\left( x ight) = \frac{1}{{{x^2}\left( {x + 1} ight)}} = \frac{A}{x} + \frac{B}{{{x^2}}} + \frac{C}{{x + 1}} = \frac{{\left( {A + C} ight){x^2} + (A + B)x + B}}{{{x^2}\left( {x + 1} ight)}}

    => \left\{ {\begin{array}{*{20}{c}} {A + C = 0} \\ {B = 1} \\ {A + B = 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {A = - 1} \\ {B = 1} \\ {B = 1} \end{array}} ight.

    => F\left( x ight) = \int {f\left( x ight)dx = \int {\left( { - \frac{1}{x} + \frac{1}{{{x^2}}} + \frac{1}{{x + 1}}} ight)dx} }

    => F\left( x ight) = - \ln \left| x ight| - \frac{1}{x} + \ln \left| {x + 1} ight| + C = \ln \left| {\frac{{x + 1}}{x}} ight| - \frac{1}{x} + C

    Khi đó: F\left( x ight) = \left\{ {\begin{array}{*{20}{c}} {\ln \left( {\dfrac{{x + 1}}{x}} ight) - \dfrac{1}{x} + {C_1}{\text{ khi x}} \in \left( {0; + \infty } ight)} \\ {\ln \left( {\dfrac{{ - x - 1}}{x}} ight) - \dfrac{1}{x} + {C_2}{\text{ khi x}} \in \left( { - 1; + \infty } ight)} \\ {\ln \left( {\dfrac{{x + 1}}{x}} ight) - \dfrac{1}{x} + {C_3}{\text{ khi x}} \in \left( { - \infty ; - 1} ight)} \end{array}} ight.

    Theo bài ra ta có: F(x) + F(-2) = 0,5

    => \left( {\ln 2 - 1 + {C_1}} ight) + \left( {\ln \frac{1}{2} + \frac{1}{2} + {C_2}} ight) = \frac{1}{2}

    => {C_1} + {C_2} = 1

    => F\left( 2 ight) + F\left( { - 3} ight) = \left( {\ln \frac{3}{2} + \frac{1}{2} + {C_1}} ight) + \left( {\ln \frac{2}{3} + \frac{1}{2} + {C_1}} ight) = \frac{5}{6}

  • Câu 6: Vận dụng

    Cho hàm số f(x) đồng biến và có đạo hàm cấp hai trên đoạn \lbrack 0;2brack và thỏa mãn 2\left\lbrack f(x) ightbrack^{2} - f(x).f''(x) + \left\lbrack f'(x) ightbrack^{2} = 0 với \forall x \in \lbrack 0;2brack. Biết rằng f(0) = 1;f(2) = e^{6} khi đó tích phân M = \int_{- 2}^{0}{(2x + 1)f(x)dx} bằng:

    Ta có:

    2\left\lbrack f(x) ightbrack^{2} - f(x).f''(x) + \left\lbrack f'(x) ightbrack^{2} = 0

    \Leftrightarrow f(x).f''(x) - \left\lbrack f'(x) ightbrack^{2} = 2\left\lbrack f(x) ightbrack^{2}

    \Leftrightarrow \frac{f(x).f''(x) - \left\lbrack f'(x) ightbrack^{2}}{\left\lbrack f(x) ightbrack^{2}} = 2

    \Leftrightarrow \left\lbrack \frac{f'(x)}{f(x)} ightbrack' = 2 \Leftrightarrow \int_{}^{}{\left\lbrack \frac{f'(x)}{f(x)} ightbrack'dx} = \int_{}^{}{2dx}

    \Leftrightarrow \frac{f'(x)}{f(x)} = 2x + C_{1} \Leftrightarrow \ln\left| f(x) ight| = x^{2} + C_{1}x + C_{2}

    Theo bài ra ta có:

    \left\{ \begin{matrix} f(0) = 1 \\ f(2) = e^{6} \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} ln1 = C_{2} \\ 4 + 2C_{1} = 6 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} C_{2} = 0 \\ C_{1} = 1 \\ \end{matrix} ight.

    \Rightarrow \ln\left| f(x) ight| = x^{2} + x \Rightarrow f(x) = e^{x^{2} + x}

    \Rightarrow M = \int_{- 2}^{0}{(2x + 1)e^{x^{2} + x}dx} = \left. \ e^{x^{2} + x} ight|_{- 2}^{0} = 1 - e^{2}

  • Câu 7: Nhận biết

    Một vật chuyển động chậm dần đều với vận tốc v(t) = 30 - 2t(m/s). Hỏi trong 5s trước khi dừng hẳn, vật di chuyển động được bao nhiêu mét?

    Khi dừng hẳn v(t) = 30 - 2t = 0 \Rightarrow t = 15(s)

    Khi đó trong 5s trước khi dừng hẳn vật di chuyển được:

    S = \int_{10}^{15}{v(t)dt} = \int_{10}^{15}{(30 - 2t)dt} = 25m.

  • Câu 8: Thông hiểu

    Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi y = \ln x,y = 0,x = e là V = \pi(a + be). Tính a + b?

    Phương trình hoành độ giao điểm \ln x = 0 \Leftrightarrow x = 1

    Ta có:

    V =\pi\int_{1}^{e}{\ln^{2}xdx}

    = \pi\left\lbrack \left. \ \left(x\ln^{2}x ight) ight|_{1}^{e} - \int_{1}^{e}{x.\frac{2}{x}.\ln xdx}ightbrack

    = \pi\left\lbrack e - 2\int_{1}^{e}{\ln xdx} ightbrack

    = \pi\left\{ e - 2.\left\lbrack \left. \ \left( x\ln x ight) ight|_{1}^{e} - \int_{1}^{e}{dx} ightbrack ight\}

    = \pi\left\{ e - 2.\lbrack e - e + 1brack ight\} = \pi(e - 2)

    Vậy a = - 2;b = 1 \Rightarrow a + b = - 1

  • Câu 9: Nhận biết

    Xét hình phẳng (H) giới hạn bởi các đường như hình vẽ (phần gạch sọc).

    Diện tích hình phẳng (H) được tính theo công thức

    Ta có:

    S = \int_{0}^{1}{\left| f(x) ight|dx} + \int_{1}^{4}{\left| g(x) ight|dx}

    = \int_{0}^{1}{f(x)dx} + \int_{1}^{4}{g(x)dx}

  • Câu 10: Nhận biết

    Tính tích phân I = \int_{0}^{1}{(2x + 1)e^{x}dx} bằng cách đặt u = 2x + 1;dv = e^{x}dx. Công thức nào dưới đây chính xác?

    Đặt \left\{ \begin{matrix} u = 2x + 1 \\ dv = e^{x}dx \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} du = 2dx \\ v = e^{x} \\ \end{matrix} ight.

    Suy ra I = \int_{0}^{1}{(2x + 1)e^{x}dx} = \left. \ \left\lbrack (2x + 1)e^{x} ightbrack ight|_{0}^{1} - 2\int_{0}^{1}{e^{x}dx}

  • Câu 11: Thông hiểu

    Một ô tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc a(t) = 6 - 2t\left( m/s^{2} ight), trong đó t là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. Hỏi quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là bao nhiêu mét?

    Ta có:

    v(t) = \int_{}^{}{a(t)dt} = \int_{}^{}{(6 - 2t)dt} = 6t - t^{2} + C

    Khi đó v_{\max} \Leftrightarrow t = 3 do ban đầu ô tô đang dừng nên v(0) = 0 \Rightarrow C = 0

    Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là: S = \int_{0}^{3}{\left( 6t - t^{2} ight)dt} = 18m.

  • Câu 12: Thông hiểu

    Một ô tô đang chạy đều với vận tốc x(m/s) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v = - 5t + 20(m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.

    a) Khi xe dừng hẳn thì vận tốc bằng 0(m/s). Đúng||Sai

    b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5\ s. Sai||Đúng

    c) \int_{}^{}{( - 5t + 20)dt =}\frac{- 5t^{2}}{2} + 20t + C. Đúng||Sai

    d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 400\ m. Sai||Đúng

    Đáp án là:

    Một ô tô đang chạy đều với vận tốc x(m/s) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v = - 5t + 20(m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.

    a) Khi xe dừng hẳn thì vận tốc bằng 0(m/s). Đúng||Sai

    b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5\ s. Sai||Đúng

    c) \int_{}^{}{( - 5t + 20)dt =}\frac{- 5t^{2}}{2} + 20t + C. Đúng||Sai

    d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 400\ m. Sai||Đúng

    a) Khi xe dừng hẳn thì vận tốc bằng 0(m/s). Mệnh đề đúng

    b) Cho v = 0 \Leftrightarrow - 5t + 20 = 0 \Leftrightarrow t\ = \ 4\ (s). Mệnh đề sai

    c) \int_{}^{}{( - 5t + 20)dt =}\frac{- 5t^{2}}{2} + 20t + C. Mệnh đề đúng

    d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là S = \int_{0}^{4}{( - 5t + 20)dt} = 40\ (m). Mệnh đề sai

  • Câu 13: Thông hiểu

    Tính diện tích hình phẳng giới hạn bởi các đường y = x\sin2x;y = 2x;x = \frac{\pi}{2}?

    Phương trình hoành độ giao điểm

    x\sin2x = 2x \Leftrightarrow \left\lbrack\begin{matrix}x = 0 \\\sin2x = 2(L) \\\end{matrix} ight.

    Diện tích hình phẳng là:

    S = \int_{0}^{\frac{\pi}{2}}{\left| x\sin x - 2x ight|dx} = \left| \int_{0}^{\frac{\pi}{2}}{\left( x\sin x - 2x ight)dx} ight|

    = \left| \left. \ \left(\frac{1}{4}\sin2x - \frac{1}{2}x\cos2x - x^{2} ight)ight|_{0}^{\frac{\pi}{2}} ight| = \frac{\pi^{2}}{4} -\frac{\pi}{4}

  • Câu 14: Nhận biết

    Tìm nguyên hàm của hàm số f(x) =\frac{e^{\tan x}}{\cos^{2}x}?

    Đặt t = \tan x \Rightarrow dt =\frac{1}{\cos^{2}x}dx

    \int_{}^{}{\frac{e^{\tan x}}{\cos^{2}x}dx} = \int_{}^{}{e^{t}dt} = e^{t} + C = e^{\tan x} +C

  • Câu 15: Nhận biết

    Nguyên hàm của hàm số f(x) = \sqrt{3x + 2} là:

    Ta có:

    \int_{}^{}{f(x)dx} = \int_{}^{}{\sqrt{3x + 2}dx} = \int_{}^{}{(3x + 2)^{\frac{1}{2}}dx}

    = \frac{(3x + 2)^{1 + \frac{1}{2}}}{1 +\dfrac{1}{2}}.\frac{1}{3} + C = \frac{2}{9}.(2x + 3).\sqrt{3x + 2} +C

  • Câu 16: Thông hiểu

    Cho hàm số f(x);g(x) là các hàm số liên tục trên \lbrack 1;3brack và thỏa mãn \int_{1}^{3}{\left\lbrack f(x) + 3g(x) ightbrack dx} = 10 và \int_{1}^{3}{\left\lbrack 2f(x) - g(x) ightbrack dx} = 6. Tính tích phân K = \int_{1}^{3}{\left\lbrack f(x) + g(x) ightbrack dx}?

    Theo bài ra ta có:

    \left\{ \begin{matrix}\int_{1}^{3}{\left\lbrack f(x) + 3g(x) ightbrack dx} = 10 \\\int_{1}^{3}{\left\lbrack 2f(x) - g(x) ightbrack dx} = 6 \\\end{matrix} ight.\Leftrightarrow \left\{ \begin{matrix}\int_{1}^{3}{f(x)dx} + 3\int_{1}^{3}{g(x)dx} = 10 \\2\int_{1}^{3}{f(x)dx} - \int_{1}^{3}{g(x)dx} = 6 \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}\int_{1}^{3}{f(x)dx} = 4 \\\int_{1}^{3}{g(x)dx} = 2 \\\end{matrix} ight.\Rightarrow K = \int_{1}^{3}{\left\lbrack f(x) +g(x) ightbrack dx} = 4.2 = 6

  • Câu 17: Vận dụng

    Cho hình phẳng (S) được giới hạn bởi đồ thị các hàm số \left( P_{1} ight):y= x^{2},\left( P_{2} ight):y = \frac{x^{2}}{4},\left( H_{1} ight):y= \frac{2}{x},\left( H_{2} ight):y = \frac{8}{x}. Tính diện tích hình phẳng (S)?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hình phẳng (S) được giới hạn bởi đồ thị các hàm số \left( P_{1} ight):y= x^{2},\left( P_{2} ight):y = \frac{x^{2}}{4},\left( H_{1} ight):y= \frac{2}{x},\left( H_{2} ight):y = \frac{8}{x}. Tính diện tích hình phẳng (S)?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Nhận biết

    Hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn \lbrack 1;3brack, trục Ox và hai đường thẳng x = 1;x = 3 có diện tích là:

    Công thức tính diện tích cần tìm là: S = \int_{1}^{3}{\left| f(x) ight|dx}.

  • Câu 19: Thông hiểu

    Hàm số F\left( x ight) = 2\sin x - 3\cos x là một nguyên hàm của hàm số nào sau đây?

     F'\left( x ight) = f\left( x ight) = 2\cos x + 3\sin x

  • Câu 20: Vận dụng

    Cho hàm số f(x) xác định trên \mathbb{R}\backslash \left\{ 1 ight\} thỏa mãn f'\left( x ight) = \frac{1}{{x - 1}};f\left( 0 ight) = 2017;f\left( 2 ight) = 2018. Giá trị của biểu thức T = \left[ {f\left( 3 ight) - 2018} ight].\left[ {f\left( { - 1} ight) - 2017} ight] là bao nhiêu?

     \begin{matrix} f\left( x ight) = \int {f'\left( x ight)dx} = \int {\dfrac{1}{{x - 1}}dx} \hfill \\ = \ln \left| {x - 1} ight| + C = \left\{ {\begin{array}{*{20}{c}} {\ln \left( {x - 1} ight) + {C_1}{\text{ khi x > 1}}} \\ {\ln \left( {1 - x} ight) + {C_2}{\text{ khi x < 1}}} \end{array}} ight. \hfill \\ \end{matrix}

    Ta có:

    \left\{ {\begin{array}{*{20}{c}} {f\left( 0 ight) = 2017 \Rightarrow \ln \left( {1 - 0} ight) + {C_2} = 2017} \\ {f\left( 2 ight) = 2018 \Rightarrow \ln \left( {2 - 1} ight) + {C_1} = 2018} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{C_2} = 2017} \\ {{C_1} = 2018} \end{array}} ight.

    Khi đó

    \begin{matrix} T = \left[ {f\left( 3 ight) - 2018} ight].\left[ {f\left( { - 1} ight) - 2017} ight] \hfill \\ = \left[ {\ln \left( {3 - 1} ight) + 2018 - 2018} ight].\left[ {\ln \left( {1 - \left( { - 1} ight)} ight) + 2017 - 2017} ight] \hfill \\ = \ln 2.\ln 2 = {\ln ^2}2 \hfill \\ \end{matrix}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 4 Nguyên hàm Tích phân CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 29 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 4 Nguyên hàm Tích phân CTST
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập