Lớp 10 Toán 10 - Kết nối tri thức

Đề kiểm tra 15 phút Chương 6 Hàm số đồ thị và ứng dụng

Mô tả thêm: Đề kiểm tra 15 phút Toán 10 Hàm số đồ thị và ứng dụng gồm 20 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Kết nối tri thức.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Tập xác định của hàm số y = \frac{\sqrt{9 - x^{2}}}{x^{2} - 6x + 8} là

    Ta có 9 − x2 ≥ 0 ⇔ (3−x)(3+x) ≥ 0 ⇔  − 3 ≤ x ≤ 3.

    Hàm số xác định khi và chỉ khi

    \left\{ \begin{matrix} 9 - x^{2} \geq 0 \\ x^{2} - 6x + 8 eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} - 3 \leq x \leq 3 \\ x eq 4 \\ x eq 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} - 3 \leq x \leq 3 \\ x eq 2 \\ \end{matrix} ight.. Vậy x ∈ [ − 3; 3] ∖ {2}.

  • Câu 2: Thông hiểu

    Phương trình \left( x^{2} + 5x + 4 ight)\sqrt{x + 3} =0 có bao nhiêu nghiệm?

    Điều kiện xác định của phương trình là x ≥  − 3.

    Phương trình tương đương với \Leftrightarrow \left\{ \begin{matrix}x \geq - 3 \\\left\lbrack \begin{matrix}x = - 1 \\x = - 4 \\x = - 3 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}x = - 1 \\x = - 3 \\\end{matrix} ight..

    Vậy phương trình có hai nghiệm.

  • Câu 3: Nhận biết

    Điểm nào sau đây thuộc đồ thị của hàm số y = \frac{x - 2}{x(x - 1)}?

    Thử trực tiếp thấy tọa độ của M(2;0) thỏa mãn phương trình hàm số.

  • Câu 4: Thông hiểu

    Phương trình \left( x^{2} - 6x ight)\sqrt{17 - x^{2}} = x^{2}- 6x có bao nhiêu nghiệm thực phân biệt?

    Điều kiện: 17 - x^{2} \geq 0\Leftrightarrow - \sqrt{17} \leq x \leq \sqrt{17}.

    Ta có: \left( x^{2} - 6x ight)\sqrt{17 -x^{2}} = x^{2} - 6x \Leftrightarrow \left( x^{2} - 6x ight)\left(\sqrt{17 - x^{2}} - 1 ight) = 0.

    \Leftrightarrow \left\lbrack\begin{matrix}x^{2} - 6x = 0 \\\sqrt{17 - x^{2}} = 1 \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}x(x - 6) = 0 \\16 - x^{2} = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}x = 0(T) \\x = 6(L) \\x = \pm 4(T) \\\end{matrix} ight..

    Vậy phương trình có 3 nghiệm thực phân biệt.

  • Câu 5: Vận dụng

    Đường gấp khúc trong hình vẽ là dạng đồ thị của một trong bốn hàm số được liệt kê trong các phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

    Đồ thị hàm số đi qua các điểm (0;1) và (1;0) nên chỉ có hàm số y = 1 − |x| thỏa mãn.

    Chọn y = 1 − |x|.

  • Câu 6: Nhận biết

    Số nghiệm thực của phương trình \sqrt{x - 1}.\sqrt{2x + 6} = x + 3 là

    ĐK: x \geq 1 , \sqrt{x - 1}.\sqrt{2x + 6} = x + 3 \Leftrightarrow(x - 1)(2x + 6) = (x + 3)^{2}\Leftrightarrow (x + 3)(x - 5) = 0\Leftrightarrow \left\lbrack \begin{matrix}x = - 3(KTM) \\x = 5(TM) \\\end{matrix} ight..

  • Câu 7: Nhận biết

    Số nghiệm của phương trình x - \sqrt{3x + 4} = 2 là:

    x - \sqrt{3x + 4} = 2 \Leftrightarrow\sqrt{3x + 4} = x - 2\Leftrightarrow \left\{ \begin{matrix}x - 2 \geq 0 \\3x + 4 = (x - 2)^{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\3x + 4 = x^{2} - 4x + 4 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\x^{2} - 7x = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\\left\lbrack \begin{matrix}x = 0 \\x = 7 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow x = 7.

    Vậy phương trình có 1 nghiệm.

  • Câu 8: Thông hiểu

    Cho bất phương trình m{x^2} - (2m - 1)x + m + 1 < 0 (1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.

    Để m{x^2} - (2m - 1)x + m + 1 < 0 thì m{x^2} - (2m - 1)x + m + 1 \geqslant 0 nghiệm đúng với \forall x \in \mathbb{R}.

    Nghĩa là:\left\{ {\begin{array}{*{20}{c}} {a > 0} \\ {\Delta \leqslant 0} \end{array}} ight.

    \begin{matrix} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {{{\left( {2m - 1} ight)}^2} - 4m\left( {m + 1} ight) \leqslant 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {4{m^2} - 4m + 1 - 4{m^2} - 4m \leqslant 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ { - 8m + 1 \leqslant 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m \geqslant \dfrac{1}{8}} \end{array}} ight. \Leftrightarrow m \geqslant \frac{1}{8} \hfill \\ \end{matrix}

  • Câu 9: Vận dụng cao

    Phương trình \sqrt{2x + 3} + \sqrt{x + 1} = 3x + 2\sqrt{2x^{2} + 5x + 3} - 16 có mấy nghiệm ?

    Điều kiện: x ≥  − 1

    Đặt t = \sqrt{2x + 3} + \sqrt{x + 1}\ \ \ (t \geq 0)\ \

    \Rightarrow t^{2} = 3x + 4 + 2\sqrt{2x^{2} + 5x + 3}

    Phương trình đã cho trở thành: t^{2} - t - 20 = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 5\ \ \ (t/m) \\ t = - 4\ \ \ \ (l) \\ \end{matrix} ight.

    Với t = 5 ta có: \sqrt{2x + 3} + \sqrt{x + 1} = 5 \Leftrightarrow x = 3

    Vậy phương trình đã cho có 1 nghiệm.

  • Câu 10: Vận dụng

    Số nghiệm của phương trình 10\sqrt{x^{3} + 1} = 3(x^{2} + 2) là:

    ĐKXĐ: x3 + 1 ≥ 0 ⇔ x ≥  − 1.

    Phương trình\Leftrightarrow 10\sqrt{(x +1)(x^{2} - x + 1)} = 3(x^{2} + 2)

    Đặt \sqrt{x + 1} = a,\ \ \sqrt{x^{2} - x +1} = b , a ≥ 0,  b ≥ 0

    Suy ra a2 + b2 = x2 + 2 khi đó

    Phương trình trở thành

    \begin{matrix}10ab = 3\left( a^{2} + b^{2} ight) \Leftrightarrow 3a^{2} - 10ab +3b^{2} = 0 \\\Leftrightarrow (3a - b)(a - 3b) = 0 \Leftrightarrow \left\lbrack\begin{matrix}3a = b \\a = 3b \\\end{matrix} ight.\ \\\end{matrix}

    Với 3a = b ta có 3\sqrt{x + 1} = \sqrt{x^{2} - x + 1}\Leftrightarrow 9(x + 1) = x^{2} - x + 1

    \Leftrightarrow x^{2} - 10x - 8 = 0\Leftrightarrow x = 5 \pm \sqrt{33} (thỏa mãn điều kiện)

    Với a = 3b ta có \sqrt{x + 1} = 3\sqrt{x^{2} - x + 1}\Leftrightarrow x + 1 = 9\left( x^{2} - x + 1 ight)

     ⇔ 9x2 − 10x + 8 = 0 (phương trình vô nghiệm).

    Vậy phương trình có nghiệm là x = 5 \pm\sqrt{33}.

  • Câu 11: Nhận biết

    Hàm số y = x2 − 4x + 11 đồng biến trên khoảng nào trong các khoảng sau đây?

    Ta có bảng biến thiên:

    Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng(2;+∞).

  • Câu 12: Thông hiểu

    Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x^{2} + 2x + 1 là:

     Xét biếu thức f(x) = x^{2} + 2x + 1 có ∆ = 0 và nghiệm là x = -{\text{ }}1;{\text{ }}a = 1 > 0

    Ta có bảng xét dấu như sau:

    Tìm bảng xét dấu của tam thức bậc hai

  • Câu 13: Nhận biết

    Cho f(x)=ax^{2}+bx+c(a≠0). Điều kiện để f(x)>0 \forall x \in \mathbb{R} là:

     Ta có: f(x)=ax^{2}+bx+c>0 \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{matrix}a>0\\ \Delta < 0\end{matrix}ight..

  • Câu 14: Thông hiểu

    Cho hàm số y = \left\{ \begin{matrix} - 2x + 1 & khi & x \leq - 3 \\ \frac{x + 7}{2} & khi & x > - 3 \\ \end{matrix} ight.. Biết f(x0) = 5 thì x0 là

    TH1. x0 ≤  − 3: Với f(x0) = 5 ⇔  − 2x0 + 1 = 5 ⇔ x0 =  − 2 (Loại).

    TH2. x0 >  − 3: Với f\left( x_{0} ight) = 5 \Leftrightarrow \frac{x_{0} + 7}{2} = 5 \Leftrightarrow x_{0} = 3 (thỏa mãn).

  • Câu 15: Vận dụng

    Phương trình mx2 − (3m+2)x + 1 = 0 có tính chất nào sau đây:

    Với m = 0 phương trình trở thành - 2x + 1 = 0 \Leftrightarrow x = \frac{1}{2} suy ra phương trình có nghiệm.

    Với m ≠ 0, ta có Δ = (3m+2)2 − 4m = 9m2 + 8m + 4.

    Vì tam thức 9m2 + 8m + 4 có am = 9 > 0,  Δ′m =  − 20 < 0 nên 9m2 + 8m + 4 > 0 với mọi m.

    Do đó phương trình đã cho luôn có nghiệm với mọi m.

  • Câu 16: Nhận biết

    Trong các hàm số sau, hàm số nào nghịch biến trên ℝ?

    Hàm số y = ax + b với a ≠ 0 nghịch biến trên ℝ khi và chỉ khi a < 0.

  • Câu 17: Nhận biết

    Trục đối xứng của parabol y =  − x2 + 5x + 3 là đường thẳng có phương trình

    Trục đối xứng của parabol y = ax2 + bx + c là đường thẳng x = - \frac{b}{2a}.

    Trục đối xứng của parabol y =  − x2 + 5x + 3 là đường thẳng x = \frac{5}{2}.

  • Câu 18: Nhận biết

    Cho tam thức bậc hai f(x) = x2 − 4x + 4. Hỏi khẳng định nào sau đây là đúng?

    Ta có: f(x) = x2 − 4x + 4 = 0 ⇔ x = 2

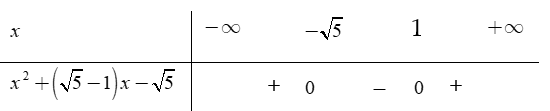
    Dựa vào bảng xét dấu, chọn đáp án f(x) > 0,  ∀x ∈ ℝ.

  • Câu 19: Thông hiểu

    Quan sát đồ thị hàm số sau:

    Cho biết hàm số nào tương ứng với đồ thị hàm số đã cho?

    Ta có:

    Đồ thị cắt trục Oy tại - 1 nên ta loại đáp án y = x^{2} + 2x - 2 và y = x^{2} - 2x - 1.

    Dễ thấy đồ thị có đỉnh là ( - 1; - 2)

    Xét hàm số y = x^{2} + 2x - 1 có đỉnh là ( - 1; - 2).

    Vậy hàm số tương ứng với đồ thị là: y = x^{2} + 2x - 1.

  • Câu 20: Vận dụng cao

    Hàm số nào sau đây có đồ thị như hình bên

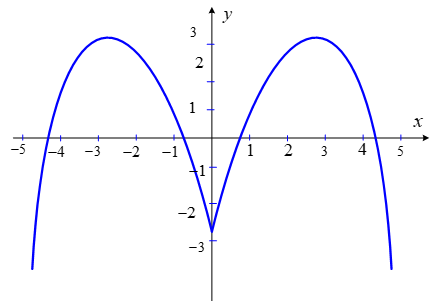
    Quan sát đồ thị ta loại y = x2 − 3x − 3 và y =  − x2 + 5x − 3. Phần đồ thị bên phải trục tung là phần đồ thị (P) của hàm số y =  − x2 + 5x − 3 với x > 0, tọa độ đỉnh của (P) là \left( \frac{5}{2};\frac{13}{4} ight), trục đối xứng là x = 2, 5. Phần đồ thị bên trái trục tung là do lấy đối xứng phần đồ thị bên phải của (P)qua trục tung Oy. Ta được cả hai phần là đồ thị của hàm số y =  − x2 + 5|x| − 3.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 6 Hàm số đồ thị và ứng dụng Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 29 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 6 Hàm số đồ thị và ứng dụng
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập