Cho hệ bất phương trình ![]() . Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình?
. Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình?
Thay lần lượt tọa độ các điểm vào hệ bất phương trình. Ta thấy chỉ có điểm thỏa mãn cả hai phương trình trong hệ
.
Cho hệ bất phương trình ![]() . Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình?
. Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình?
Thay lần lượt tọa độ các điểm vào hệ bất phương trình. Ta thấy chỉ có điểm thỏa mãn cả hai phương trình trong hệ
.
Phần không bị gạch chéo là nghiệm của bất phương trình nào? (kể cả bờ ![]() )
)
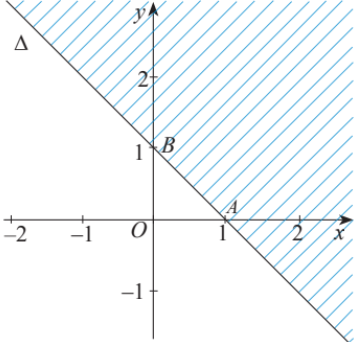
Đường thẳng có dạng
đi qua hai điểm
và
.
Thay tọa độ hai điểm này vào :
.
Vậy có dạng
.
Thay điểm vào
:
. Suy ra phần không gạch chéo (không chứa
) là nghiệm của bất phương trình
.
Cặp số nào sau đây là nghiệm của bất phương trình ![]() ?
?
Thay các cặp số vào bất phương trình ta thấy là nghiệm của bất phương trình đã cho.
Miền nghiệm của bất phương trình ![]() chứa điểm nào dưới đây?
chứa điểm nào dưới đây?
Xét điểm . Ta có:
thỏa mãn. Do đó miền nghiệm của bất phương trình
chứa điểm
.
Tìm m để hệ bất phương trình sau trở thành hệ bất phương trình bậc nhất hai ẩn:  .
.
Để hệ bất phương trình trở thành hệ bất phương trình bậc nhất hai ẩn thì hệ số đứng trước
phải bằng
nghĩa là:
Vậy với thì hệ bất phương trình đã cho trở thành hệ bất phương trình bậc nhất hai ẩn.
Cho hệ bất phương trình ![]() . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
Với . Ta có:
. Cả hai bất phương trình đều thỏa mãn. Chọn đáp án này.
Điểm ![]() thuộc miền nghiệm của hệ bất phương trình nào sau đây?
thuộc miền nghiệm của hệ bất phương trình nào sau đây?
Thay tọa độ lần lượt vào từng phương trình của hệ
ta thấy thỏa mãn.
Điểm nào sau đây thuộc miền nghiệm của bất phương trình ![]() ?
?
Xét điểm . Ta có:
nên
thuộc miền nghiệm của bất phương trình đã cho.
Điền vào chỗ trống từ còn thiếu: “Trong mặt phẳng tọa độ Oxy, tập hợp các điểm ![]() sao cho
sao cho ![]() được gọi là ……của bất phương trình
được gọi là ……của bất phương trình ![]() ”.
”.
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm sao cho
được gọi là miền nghiệm của bất phương trình
.
Tìm tất cả giá trị của tham số ![]() để hệ bất phương trình
để hệ bất phương trình  có tập nghiệm được biểu diễn trên mặt phẳng tọa độ là một hình tam giác.
có tập nghiệm được biểu diễn trên mặt phẳng tọa độ là một hình tam giác.
Họ đường thẳng luôn đi qua điểm
, hay nói cách khác các đường thẳng
xoay quanh A.
Mặt khác, ta có đúng với mọi m
=> Miền nghiệm của bất phương trình luôn chứa điểm
.
Do đó ta có 3 khả năng sau
Vậy .
Miền nghiệm của hệ bất phương trình  chứa điểm nào trong các điểm sau đây?
chứa điểm nào trong các điểm sau đây?
Với . Ta có:
. Cả ba bất phương trình đều đúng. Chọn đáp án này.
Phần nữa mặt phẳng tô đậm (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?
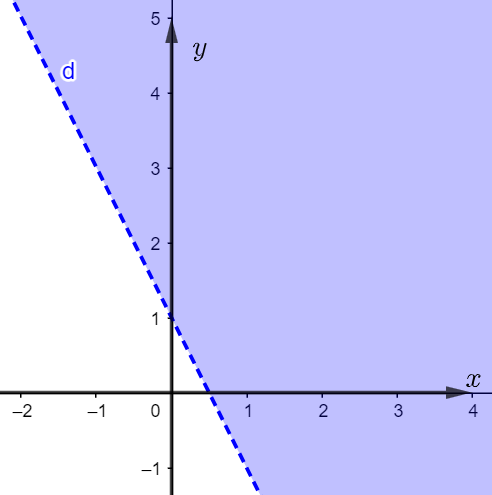
Đường thẳng d đi qua hai điểm và
nên nó là đường thẳng
Xét điểm . Thay tọa độ
vào d ta được:
. Suy ra miền tô đậm (không chứa d) là miền nghiệm của bất phương trình
.
Miền nghiệm của hệ bất phương trình  chứa điểm nào sau đây?
chứa điểm nào sau đây?
Ta thấy là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
thuộc cả ba miền nghiệm của ba bất phương trình.
Nửa mặt phẳng là miền nghiệm của bất phương trình ![]() không chứa điểm nào trong các điểm sau:
không chứa điểm nào trong các điểm sau:
Thay điểm vào bất phương trình, ta được:
(sai). Do đó điểm này không thuộc miền nghiệm của bất phương trình.
Câu 1câu 2
Câu 1câu 2
Điểm ![]() là điểm thuộc miền nghiệm của bất phương trình:
là điểm thuộc miền nghiệm của bất phương trình:
Vì là mệnh đề đúng nên
là điểm thuộc miền nghiệm của bất phương trình
.
Cho hệ bất phương trình  có miền nghiệm là miền ngũ giác
có miền nghiệm là miền ngũ giác ![]() như hình dưới. Giá trị nhỏ nhất của
như hình dưới. Giá trị nhỏ nhất của ![]() là:
là:
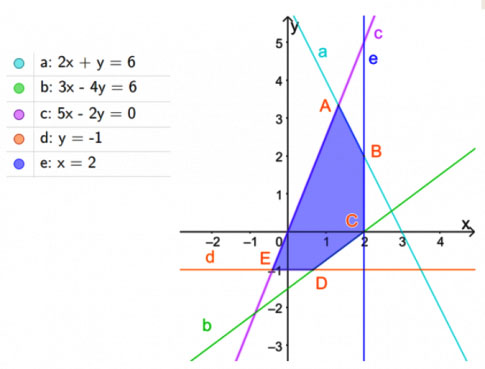
Đầu tiên học sinh xác định tọa độ các đỉnh đa giác.
Tọa độ đỉnh A là tọa độ giao điểm hai đường thẳng a và c
=> Tọa độ điểm A là nghiệm của hệ phương trình:
Tọa độ đỉnh B là tọa độ giao điểm hai đường thẳng a và e
=> Tọa độ điểm B là nghiệm của hệ phương trình:
Tọa độ đỉnh D là tọa độ giao điểm hai đường thẳng b và d
=> Tọa độ điểm D là nghiệm của hệ phương trình:
Tọa độ đỉnh E là tọa độ giao điểm hai đường thẳng d và e
=> Tọa độ điểm E là nghiệm của hệ phương trình:
Ta phải tìm các giá trị x, y thỏa mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị nhỏ nhất của biểu thức F trên miền tứ giác ABCDE.
Tính các giá trị của biểu thức tại các đỉnh của đa giác.
Tại ta có:
Tại ta có:
Tại ta có:
Tại ta có:
Tại ta có:
F đạt giá trị nhỏ nhất bằng -114 tại
Cặp nghiệm nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: ![]() ?
?
=>
thay vào bất phương trình ta có:
=> Đáp án sai
=>
thay vào bất phương trình ta có:
=> Đáp án sai
=>
thay vào bất phương trình ta có:
=> Đáp án sai
=>
thay vào bất phương trình ta có:
=> Đáp án đúng
Vậy là nghiệm của bất phương trình bậc nhất hai ẩn:
Miền nghiệm của hệ bất phương trình  chứa điểm nào trong các điểm sau đây?
chứa điểm nào trong các điểm sau đây?
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Với . Bất phương trình thứ nhất sai nên không thỏa mãn.
Với . Đúng.
Một cửa hàng bán hai loại mặt hàng ![]() và
và ![]() . Biết rằng cứ bán một mặt hàng loại
. Biết rằng cứ bán một mặt hàng loại ![]() cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại
cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại ![]() cửa hàng lãi 7 nghìn đồng. Gọi
cửa hàng lãi 7 nghìn đồng. Gọi ![]() lần lượt là số mặt hàng loại
lần lượt là số mặt hàng loại ![]() và mặt hàng loại
và mặt hàng loại ![]() mà cửa hàng đó bán ra trong một tháng. Cặp số
mà cửa hàng đó bán ra trong một tháng. Cặp số ![]() nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng?
nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng?
Đặt x là số tiền lãi của mặt hàng A
y là số tiền lãi của mặt hàng B
Đổi 30 triệu = 30 000 nghìn đồng
Theo đề bài ta có:
TH1: Thay A (1000; 2000) vào phương trình
. Thay B(3000; 1000
vào phương trình
: Thay C
vào phương trình
TH4: Thay vào phương trình
Vậy đáp án là: C
