Cho hình vẽ sau là đồ thị của ba hàm số ![]() với
với ![]() và
và ![]() là các số thực cho trước, mệnh đề nào sau đây đúng?
là các số thực cho trước, mệnh đề nào sau đây đúng?
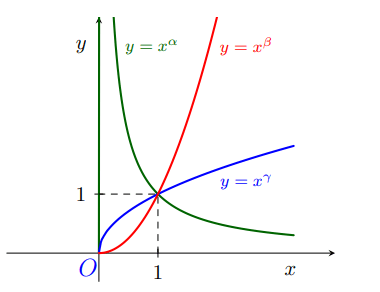
Hàm số nghịch biến trên
Các hàm số đồng biến nên
Tại thì
Cho hình vẽ sau là đồ thị của ba hàm số ![]() với
với ![]() và
và ![]() là các số thực cho trước, mệnh đề nào sau đây đúng?
là các số thực cho trước, mệnh đề nào sau đây đúng?

Hàm số nghịch biến trên
Các hàm số đồng biến nên
Tại thì
Cho ![]() . Rút gọn biểu thức
. Rút gọn biểu thức 
Ta có:
Cho biết ![]() . Tính
. Tính
![]()
Ta có:
Giá trị của biểu thức ![]() là:
là:
Ta có:
Cho ![]() ; (
; (![]() là phân số tối giản). Tính giá trị biểu thức
là phân số tối giản). Tính giá trị biểu thức ![]() .
.
Ta có:
Cho hàm số ![]() . Cho các khẳng định sau:
. Cho các khẳng định sau:
i) Hàm số xác định với mọi x
ii) Đồ thị hàm số luôn đi qua điểm (1; 1)
iii) Hàm số nghịch biến trên ![]()
iv) Đồ thị hàm số có hai đường tiệm cận
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
Ta có khẳng định ii) và iv) là đúng
i) Sai vì hàm số đã cho xác định khi x > 0
iii) Sai vì hàm số nghịch biến trên
Hàm số ![]() có tập xác định là:
có tập xác định là:
Hàm số có số mũ nguyên âm xác định khi
Hàm số xác định khi
Vậy tập xác định là:
Với a là một số thực dương thì biểu thức  được rút gọn là:
được rút gọn là:
Ta có:
Cho đồ thị hàm số ![]() . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
Theo định nghĩa của hàm số lũy thừa, đồ thị hàm số có tiệm cận đứng là x = 0
Ta có: suy ra đồ thị hàm số có tiệm cận ngang là y = 0
Vậy đồ thị hàm số có tiệm cận ngang là y = 0 và tiệm cận đứng là x = 0
Cho ![]() , viết
, viết ![]() về dạng
về dạng ![]() và
và ![]() về dạng
về dạng ![]() . Tình giá trị biểu thức
. Tình giá trị biểu thức ![]()
Ta có:
Cho biểu thức ![P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6}](https://i.khoahoc.vn/data/image/holder.png) với a và b là các số thực dương. Khẳng định nào sau đây là đúng?
với a và b là các số thực dương. Khẳng định nào sau đây là đúng?
Thực hiện thu gọn biểu thức như sau:
Cho hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Đồ thị hàm số có đường tiệm cận đứng x = 1
Tính đạo hàm của hàm số ![]()
Ta có:
Tính đạo hàm của hàm số ![]()
Ta có:
Khẳng định nào dưới đây đúng?
Ta có:
Vậy đáp án đúng là:
Biết ![\sqrt[5]{{\frac{b}{a}\sqrt[3]{{\frac{a}{b}}}}} = {\left( {\frac{a}{b}} ight)^m}](https://i.khoahoc.vn/data/image/holder.png) với a và b là các số thực dương. Tìm m?
với a và b là các số thực dương. Tìm m?
Ta có:
Rút gọn biểu thức ![P = \frac{{{x^{\frac{1}{6}}}.\sqrt[3]{{{x^4}}}.\sqrt[4]{{{x^5}}}}}{{\sqrt {{x^3}} }}](https://i.khoahoc.vn/data/image/holder.png) với x > 0
với x > 0
Ta có:
Biết rằng ![]() với x > 0. Tìm n?
với x > 0. Tìm n?
Ta có:
Vậy
Cho hàm số ![]() . Tính
. Tính ![]()
Ta có:
Tìm tất cả các tập giá trị của a để ![]() ?
?
Ta có:
=>
Mà 5 < 6 =>
