Xét tính đúng, sai của các phát biểu sau?
Tập  là tập xác định của hàm số
là tập xác định của hàm số  . Đúng||Sai
. Đúng||Sai
Số nghiệm của phương trình  trên khoảng
trên khoảng  là 3 nghiệm.Sai||Đúng
là 3 nghiệm.Sai||Đúng
Có 5 giá trị nguyên của tham số m để phương trình  có nghiệm. Đúng||Sai
có nghiệm. Đúng||Sai
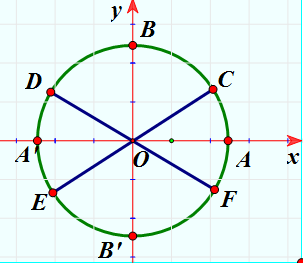
Số vị trí biểu diễn của phương trình  trên đường tròn lượng giác là 3.Sai||Đúng
trên đường tròn lượng giác là 3.Sai||Đúng
Đáp án là:
Xét tính đúng, sai của các phát biểu sau?
Tập  là tập xác định của hàm số
là tập xác định của hàm số  . Đúng||Sai
. Đúng||Sai
Số nghiệm của phương trình  trên khoảng
trên khoảng ) là 3 nghiệm.Sai||Đúng
là 3 nghiệm.Sai||Đúng
Có 5 giá trị nguyên của tham số m để phương trình  có nghiệm. Đúng||Sai
có nghiệm. Đúng||Sai
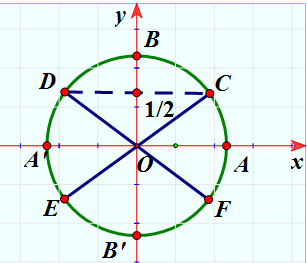
Số vị trí biểu diễn của phương trình %20%3D%0A%5Cfrac%7B1%7D%7B2%7D) trên đường tròn lượng giác là 3.Sai||Đúng
trên đường tròn lượng giác là 3.Sai||Đúng
a) Điều kiện xác định của hàm số  là:
là:
)
b) Ta có:
%20%3D%200)
%20%3D%200%20%5CLeftrightarrow%20x%20%3D%20-%20%5Cfrac%7B%5Cpi%7D%7B4%7D%20%2B%0Ak%5Cpi%3B%5Cleft(%20k%5Cmathbb%7B%5Cin%20Z%7D%20%5Cright))
Vì %20%5CRightarrow%200%20%3C%20-%0A%5Cfrac%7B%5Cpi%7D%7B4%7D%20%2B%20k%5Cpi%20%3C%20%5Cpi)
 mà
mà  suy ra
suy ra 
Vậy phương trình đã cho chỉ có 1 nghiệm thuộc khoảng ) .
.
c) Ta có: 
Phương trình đã cho có nghiệm khi và chỉ khi


Mà 
Vậy có 5 giá trị nguyên của tham số m thỏa mãn điều kiện bài toán.
d) Ta có:
%20%3D%0A%5Cfrac%7B1%7D%7B2%7D%20%5CLeftrightarrow%20%5Csin%5Cleft(%20x%20-%20%5Cfrac%7B2%5Cpi%7D%7B3%7D%20%5Cright)%20%3D%0A%5Csin%5Cleft(%20%5Cfrac%7B%5Cpi%7D%7B6%7D%20%5Cright))
)
)
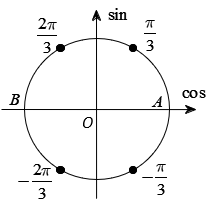
Số điểm biểu diễn mỗi họ nghiệm là số vị trí biểu diễn nghiệm của phương trình %20%3D%20%5Cfrac%7B1%7D%7B2%7D) trên đường tròn lượng giác là 2.
trên đường tròn lượng giác là 2.
![]() .
..
.