Cho hình hộp ![]() . Tìm mặt phẳng song song với mặt phẳng
. Tìm mặt phẳng song song với mặt phẳng ![]() .
.
Hình vẽ minh họa
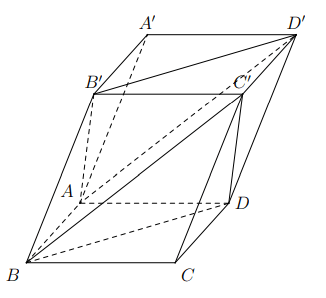
Ta có là hình bình hành nên
Tương tự ta có . Từ đó suy ra
và
.
Vậy
Cho hình hộp ![]() . Tìm mặt phẳng song song với mặt phẳng
. Tìm mặt phẳng song song với mặt phẳng ![]() .
.
Hình vẽ minh họa

Ta có là hình bình hành nên
Tương tự ta có . Từ đó suy ra
và
.
Vậy
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh BA, BC và K là một điểm bất kỳ trên cạnh BC. Gọi I là giao điểm của EF và CD.
a) Giao tuyến của (SEF) và (SCD) là đường thẳng SI.Đúng||Sai
b) Giao tuyến của (EFK) và (SAC) là đường thẳng qua K và song song với EF và AC.Đúng||Sai
c) Giao tuyến của (SBC) và (SAD) là đường thẳng qua S và song song với AD và BC. Đúng||Sai
d) Đường thẳng AB song song với măt phẳng (SFD). Sai||Đúng
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh BA, BC và K là một điểm bất kỳ trên cạnh BC. Gọi I là giao điểm của EF và CD.
a) Giao tuyến của (SEF) và (SCD) là đường thẳng SI.Đúng||Sai
b) Giao tuyến của (EFK) và (SAC) là đường thẳng qua K và song song với EF và AC.Đúng||Sai
c) Giao tuyến của (SBC) và (SAD) là đường thẳng qua S và song song với AD và BC. Đúng||Sai
d) Đường thẳng AB song song với măt phẳng (SFD). Sai||Đúng
Hình vẽ minh họa
a) Ta có:
Trong có
Từ (1) và (2) suy ra
b) Ta có:
do EF là đường trung bình trong tam giác ABC
c) Chọn chứa
Ta có:
d) Đường thẳng AB song song với măt phẳng (SFD) sai.
Cho hình lập phương ![]() cạnh
cạnh ![]() . Mặt phẳng
. Mặt phẳng ![]() đi qua tâm của hình lập phương và song song với
đi qua tâm của hình lập phương và song song với ![]() . Xác định các giao tuyến của mặt phẳng
. Xác định các giao tuyến của mặt phẳng ![]() và tứ diện
và tứ diện ![]() . Hình tạo bởi các giao tuyến đó có diện tích bằng bao nhiêu?
. Hình tạo bởi các giao tuyến đó có diện tích bằng bao nhiêu?

Hình vẽ minh họa:
Gọi I là tâm của hình lập phương
=> I là trung điểm của AC’.
Gọi (P) là mặt phẳng qua I và song song với (ABC).
Khi đó (P) cắt các đường thẳng AB’, B’C, CD’, AD’ lần lượt tại các trung điểm M, N, P, Q.
Khi đó
=> Hình tạo bởi các giao tuyến của mặt phẳng và tứ diện
là hình thoi MNPQ cạnh bằng
Mặt khác
Diện tích hình thoi MNPQ là
Hình biểu diễn của một tam giác đều là hình nào sau đây?
Hình biểu diễn của một tam giác đều là hình tam giác.
Trong không gian, cho ba đường thẳng ![]() không đồng phẳng đôi một cắt nhau. Tìm số giao điểm phân biệt của ba đường thẳng.
không đồng phẳng đôi một cắt nhau. Tìm số giao điểm phân biệt của ba đường thẳng.
Giả sử ba đường thẳng đôi một cắt lần lượt
phân biệt và tạo thành mặt phẳng
.
=> cùng nằm trên một mặt phẳng (trái giả thiết).
=> trùng nhau, tức là
đồng quy.
Vậy có duy nhất một giao điểm phân biệt của ba đường thẳng đã cho.
Khẳng định nào sau đây là đúng?
Khẳng định đúng: "Hình biểu diễn của một đường tròn là một đường elip."
Cho tứ diện ![]() . Các cạnh
. Các cạnh ![]() có trung điểm lần lượt là
có trung điểm lần lượt là ![]() . Bốn điểm nào sau đây không cùng thuộc một mặt phẳng?
. Bốn điểm nào sau đây không cùng thuộc một mặt phẳng?
Hình vẽ minh họa
Ta có:
,
=> MPNQ là hình bình hành
=> thuộc một mặt phẳng.
,
=> MRNS là hình bình hành
=> thuộc một mặt phẳng.
,
=> PSQR là hình bình hành nên P, Q, R, S thuộc một mặt phẳng.
Vậy không thuộc cùng một mặt phẳng.
Cho hình chóp tứ giác ![]() , đáy
, đáy ![]() là tứ giác (
là tứ giác (![]() không song song với
không song song với ![]() ),
), ![]() . Lấy
. Lấy ![]() là trung điểm của
là trung điểm của ![]() , lấy
, lấy ![]() sao cho
sao cho ![]() . Khi đó các cặp cạnh nào dưới đây cắt nhau?
. Khi đó các cặp cạnh nào dưới đây cắt nhau?
Hình vẽ minh hoạ
Các cặp đường thẳng SO và AD, MN và SC, SA và BC là các cặp đường thẳng chéo nhau.
Hai đường thẳng MN và SO nằm trên cùng mặt phẳng và là hai đường thẳng cắt nhau.
Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành. Gọi
là hình bình hành. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Gọi
. Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Tính tỉ số
. Tính tỉ số ![]() .
.
Đáp án: 1
Cho hình chóp có đáy
là hình bình hành. Gọi
lần lượt là trung điểm của
và
. Gọi
là trung điểm của
. Gọi
là giao điểm của
và
. Tính tỉ số
.
Đáp án: 1
Hình vẽ minh họa
-Ta có .
Trong mặt phẳng , gọi
Suy ra .
Ta có:
-Trong mp , gọi
.
Ta có .
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?
Hình vẽ minh họa
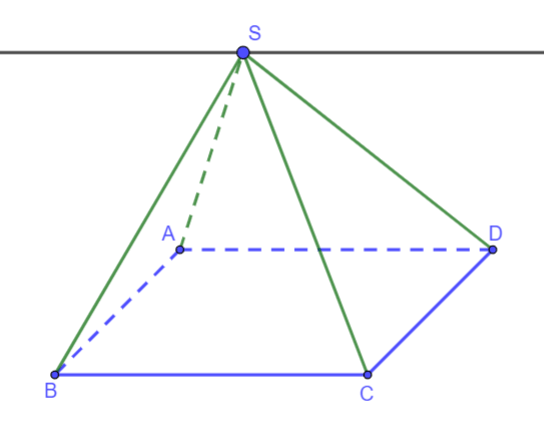
Xét (SAD) và (SBC) có:
S là điểm chung
=> Giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD
Cho hình chóp ![]() có đáy
có đáy ![]() là hình thang
là hình thang ![]() . Lấy một điểm
. Lấy một điểm ![]() thuộc cạnh
thuộc cạnh ![]() . Mặt phẳng
. Mặt phẳng ![]() qua M song song với SA và BC. Giả sử
qua M song song với SA và BC. Giả sử ![]() . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
Hình vẽ minh họa
Ta có:
Trong mặt phẳng (ABCD) kéo dài AD cắt MN tại E.
Ta lại có: suy ra
Cho hình chóp S.ABCD với đáy là hình thang ABCD, đáy lớn BC gấp đôi đáy nhỏ AD. Gọi E là trung điểm AD và O là giao điểm của AC và BE, I là một điểm thuộc đoạn OC (I khác O và C). Mặt phẳng (α) qua I song song với (SBE). Xác định hình tạo bởi các giao tuyến của mặt phẳng (α) với hình chóp S.ABCD.
Hình vẽ minh họa
Ta có:
=> => Ix cắt BC tại M, AD tại Q.
Ta có:
=>
=> Mx cắt SC tại N.
Ta có:
=>
=> Qx cắt SD tại P
Tứ giác BCDE là hình bình hành
=> CD // BE // MQ
=> CD // (α).
Ta có:
=>
Vậy hình tạo bởi các giao tuyến của mặt phẳng (α) với hình chóp S.ABCD là hình thang MNPQ.
Trong không gian cho các đường thẳng a, b và các mặt phẳng (α), (β). Trong các khẳng định sau đây, đâu là khẳng định đúng?
Mệnh đề “a // (β) và (β) // b thì a // b” là sai vì a và b có thể cắt nhau.
Mệnh đề “a // b và b ⊂ (α) thì a // (α)” là sai vì có thể a ⊂ (α).
Mệnh đề “a // b và b // (α) thì a // (α)” là sai vì có thể a ⊂ (α).
Cho mặt phẳng ![]() và hai đường thẳng
và hai đường thẳng ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Xét phương án “Nếu và
thì
” ta có:
Nếu thì
hoặc
chéo
, vậy phương án sai.
Xét phương án “Nếu và
thì
.” ta có:
Nếu thì
hoặc
, vậy phương án sai.
Xét phương án “Nếu và
thì
.” ta có:
Nếu , vậy phương án đúng.
Xét phương án “Nếu và
thì
” ta có:
Nếu thì
hoặc
chéo
hoặc
cắt
, vậy phương án sai.
Có duy nhất một mặt phẳng đi qua
Phương án "Hai đường thẳng " sai vì nếu 2 đường thẳng đó trùng nhau thì có vô số mặt phẳng đi qua 2 đường thẳng đó.
Phương án "Một điểm và một đường thẳng" sai vì nếu điểm đó thuộc đường thẳng đã cho thì có vô số mặt phẳng đi qua điểm và đường thẳng đã cho.
Phương án "Ba điểm" sai vì nếu có 2 trong ba điểm đó trùng nhau hoặc cả 3 điểm đó trùng nhau thì có vô số mặt phẳng thỏa mãn.
Vậy hoàn thành mệnh đề như sau: "Có duy nhất một mặt phẳng đi qua hai đường thẳng cắt nhau."
Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?
Phương án "Trong 4 điểm đã cho không có ba điểm nào thẳng hàng." đúng vì nếu có ba điểm thẳng hàng ( giả sử là A; B; C) thì bốn điểm đã cho luôn thuộc mặt phẳng chứa điểm D còn lại và đường thẳng AB. (mâu thuẫn giả thiết)
Phương án "Số mặt phẳng đi qua 3 trong 4 điều đã cho là 4." đúng. Số mặt phẳng đi qua 3 trong 4 điểm đã cho là:
Phương án "Số đoạn thẳng nối hai điểm trong 4 điểm đã cho là 6." đúng. Số đoạn thẳng nối 2 điểm trong 4 điểm đã cho là:
Vậy phát biểu sai là: "Trong 4 điểm đã cho luôn luôn tồn tại 3 điểm thẳng hàng."
Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
Theo tính chất của phép chiếu song song ta thấy:
Hình chiếu của hình chữ nhật không thể là hình thang có hai đáy không bằng nhau.
Cho hình chóp ![]() có đáy là hình bình hành. Qua
có đáy là hình bình hành. Qua ![]() kẻ
kẻ ![]() lần lượt song song với
lần lượt song song với ![]() . Gọi
. Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Các mệnh đề sau đúng hay sai?
. Các mệnh đề sau đúng hay sai?
a) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Sai||Đúng
. Sai||Đúng
b) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Sai||Đúng
. Sai||Đúng
c) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Đúng||Sai
. Đúng||Sai
d) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Sai||Đúng
. Sai||Đúng
Cho hình chóp có đáy là hình bình hành. Qua
kẻ
lần lượt song song với
. Gọi
là giao điểm của
và
. Các mệnh đề sau đúng hay sai?
a) Giao tuyến của và
là đường thẳng
. Sai||Đúng
b) Giao tuyến của và
là đường thẳng
. Sai||Đúng
c) Giao tuyến của và
là đường thẳng
. Đúng||Sai
d) Giao tuyến của và
là đường thẳng
. Sai||Đúng
Hình vẽ minh họa
Ta có:
với
.
Kết luận:
|
a) Sai |
b) Sai |
c) Đúng |
d) Sai |
Cho hình chóp ![]() . Trên các cạnh
. Trên các cạnh ![]() và
và ![]() lần lượt lấy các điểm
lần lượt lấy các điểm ![]() sao cho
sao cho ![]() . Hỏi
. Hỏi ![]() song song với mặt phẳng nào dưới đây?
song song với mặt phẳng nào dưới đây?
Hình vẽ minh họa:
Ta có: là đường trung bình của tam giác ABD suy ra MN//BD
Mặt khác
Cho bốn điểm không đồng phẳng trong không gian. Hỏi từ các điểm đã cho có thể xác định được bao nhiêu mặt phẳng phân biệt?
Vì 4 điểm không đồng phẳng tạo thành một tứ diện mà tứ diện có 4 mặt.
