Cho một khối chóp có diện tích đáy bằng ![]() , chiều cao bằng
, chiều cao bằng ![]() . Thể tích khối chóp đã cho là:
. Thể tích khối chóp đã cho là:
Ta có:
Thể tích khối chóp là:
Cho một khối chóp có diện tích đáy bằng ![]() , chiều cao bằng
, chiều cao bằng ![]() . Thể tích khối chóp đã cho là:
. Thể tích khối chóp đã cho là:
Ta có:
Thể tích khối chóp là:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng (ABCD) (tham khảo hình vẽ). Khẳng định nào sau đây đúng?
Hình vẽ minh họa:
Từ giả thiết ABCD là hình vuông và SB vuông góc với đáy
Ta có:
Cho hình chóp ![]() có
có ![]() . Kết luận nào sau đây sai về góc giữa
. Kết luận nào sau đây sai về góc giữa ![]() và
và ![]()
Vì nên AB là hình chiếu của SB trên (ABC)
Vậy .
Cho hình chóp ![]() có
có ![]() là hình vuông cạnh
là hình vuông cạnh ![]() ;
; ![]() . Khoảng cách giữa hai đường thẳng
. Khoảng cách giữa hai đường thẳng ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
Dựng
Dựng . Dễ thấy
Cho hình chóp tứ giác đều ![]() , cạnh đáy bằng
, cạnh đáy bằng ![]() , đường cao bằng
, đường cao bằng ![]() . Giả sử
. Giả sử ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Hình vẽ minh họa
Gọi , M là trung điểm của CD.
Ta có:
Trong tam giác SMO có
Cho hình chóp tam giác ![]() có
có ![]() vuông tại
vuông tại ![]() và
và ![]() . Kẻ đường cao
. Kẻ đường cao ![]() của tam giác
của tam giác ![]() . Khẳng định nào dưới đây là khẳng định sai?
. Khẳng định nào dưới đây là khẳng định sai?
Hình vẽ minh họa
Ta có:
Ta có:
Mà
Vậy khẳng định sai là: “”.
Cho một khối chóp tứ giác đều có cạnh đáy bằng ![]() , biết độ dài cạnh bên và cạnh đáy tỉ lệ
, biết độ dài cạnh bên và cạnh đáy tỉ lệ ![]() . Tính thể tích V của khối chóp?
. Tính thể tích V của khối chóp?
Hình vẽ minh họa
Gọi là tâm hình vuông
Ta có: tam giác SAC cân, O là trung điểm của AC nên
Tương tự tam giác SBD cân, O là trung điểm của BD nên
Trong tam giác SOC vuông tại O ta có:
Vậy thể tích hình chóp là:
Chọn khẳng định đúng trong các khẳng định sau?
Ta có:
“Trong không gian hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau” sai do hai đường thẳng phân biệt cùng vuông góc với một đường thẳng có thể cắt nhau hoặc chéo nhau.
“Trong không gian hai mặt phẳng cùng vuông góc với một đường thẳng thì song song với nhau” sai do hai mặt phẳng cùng vuông góc với một đường thẳng có thể trùng nhau.
“Trong không gian hai đường thẳng không có điểm chung thì song song với nhau” sai do trong không gian hai đường thẳng không có điểm chung có thể chéo nhau.
Vậy khẳng định đúng là: “Trong không gian hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.”
Cho hình chóp ![]() có đường thẳng
có đường thẳng ![]() vuông góc với đáy
vuông góc với đáy ![]() ,
, ![]() . Khoảng cách từ điểm
. Khoảng cách từ điểm ![]() đến đường thẳng
đến đường thẳng ![]() bằng:
bằng:
Vì vuông góc với đáy
nên
Cho hình lập phương ABCD.A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và điểm M thuộc đoạn OI sao cho MO = 2MI (tham khảo hình vẽ). Khi đó sin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng:

Hình ảnh minh họa:
Do AB // C’D’ nên giao tuyến của (MAB) và (MC’D’) là đường thẳng ∆ // AB // C’D’.
Gọi P, Q lần lượt là trung điểm của D’C’ và AB ta có:
=> MP ⊥ ∆, MQ ⊥ ∆.
Như vậy góc giữa (MAB) và (MC0’’) là góc giữa MP và MQ.
Không mất tính tổng quát, ta cho cạnh hình lập phương là 6.
Khi đó
Áp dụng định lí cosin cho tam giác MPQ ta được:
Góc α là góc giữa hai mặt phẳng (MC’D’) và (MAB) ta có:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a. Cạnh bên SA vuông góc với (ABCD), góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 30◦ . Tìm khoảng cách từ A đến mặt phẳng (SBC).
Ta có:
Gọi H là chân đường cao lên cạnh SB. Khi đó, ta có
d(A, (SBC)) = AH. sin 30◦ => AH = AB . sin 30◦ =
Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau và AB = a, BC = b, CD = c. Độ dài đoạn thẳng AD bằng bao nhiêu?
Hình vẽ minh họa:
Ta có:
=> Tam giác ABD vuông tại B.
Ta có:
=> Tam giác BCD vuông tại C.
Ta có:
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, SA ⊥ (ABCD). Góc giữa SC và mặt phẳng (ABCD) là góc giữa
Hình vẽ minh họa:
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
Do đó góc giữa SC và mặt phẳng (ABCD) là góc giữa SC và AC.
Cho hình lăng trụ đứng ABC.A’B’C’ có cạnh bên ![]() . Biết đáy ABC là tam giác vuông có BA = BC = a, gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.
. Biết đáy ABC là tam giác vuông có BA = BC = a, gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.
Hình vẽ minh họa:
Gọi N là trung điểm của BB’ => MN // B’C
=> B’C // (AMN)
=> d(AM, B’C) = d(B’C, (AMN)) = d(B’, (AMN)) = d(B, (AMN))
Kẻ BH ⊥ AM, BK ⊥ HN
=> BK ⊥ (AMN)
=> d(AM, B’C) = d(B, (AMN)) = BK
Ta có:
Ta có:
Do tam giác ABM vuông tại B
Cho tam giác ABC vuông tại A và có hai đỉnh B và C nằm trên mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của đỉnh A lên mặt phẳng (P). Trong các mệnh đề sau mệnh đề nào đúng?
=> Góc BA’C là góc tù.
Cho hình chóp O.ABC có OA = OB = OC = 1, các cạnh OB, OC, OA đối một vuông góc. Gọi M là trung điểm của AB. Tính góc giữa hai vecto ![]() ?
?
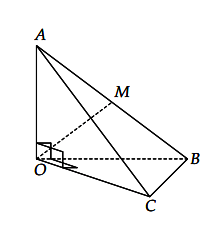
Ta có:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a. Giả sử góc BAD bằng 600. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng:
Hình vẽ minh họa
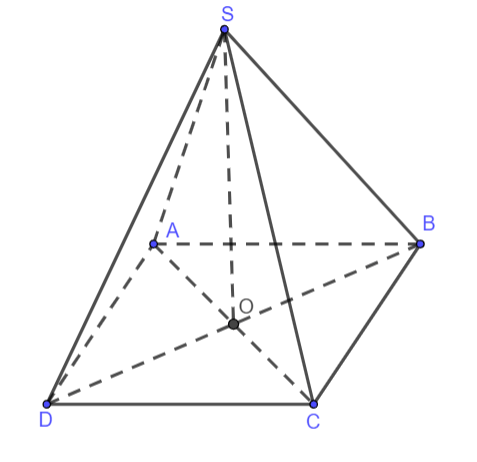
Từ S vẽ SO ⊥ (ABCD) ⇒ OA = OB = OC (là hình chiếu của các đường xiên bằng nhau) ⇒ O là tâm đường tròn ngoại tiếp đáy
Cho hình chóp S.ABCD có ABCD là hình vuông, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm BC. Gọi ![]() là góc hợp bởi đường thẳng SA và mặt phẳng (SDM). Tính
là góc hợp bởi đường thẳng SA và mặt phẳng (SDM). Tính ![]()
+ Không mất tính tổng quát, đặt AB = 2
+ Gọi N là trung điểm AB suy ra
+ Gọi
Gọi
+ Ta có
+ Ta có
+ Gọi NH là đường cao
+ Tam giác NJI đồng dạng tam giác MBJ
+ Tam giác SAB là tam giác đều cạnh bằng 2
Thể tích khối hộp chữ nhật có ba kích thước là ![]() bằng:
bằng:
Thể tích cần tìm là:
Cho tứ diện ![]() có
có ![]() . Gọi trung điểm của các cạnh
. Gọi trung điểm của các cạnh ![]() lần lượt là
lần lượt là ![]() . Biết rằng
. Biết rằng ![]() . Tính
. Tính ![]() ?
?
Hình vẽ minh họa
Đặt
Vì trung điểm của các cạnh lần lượt là
Suy ra
Từ đó
Suy ra tam giác GEF vuông tại G.
Vì nên
