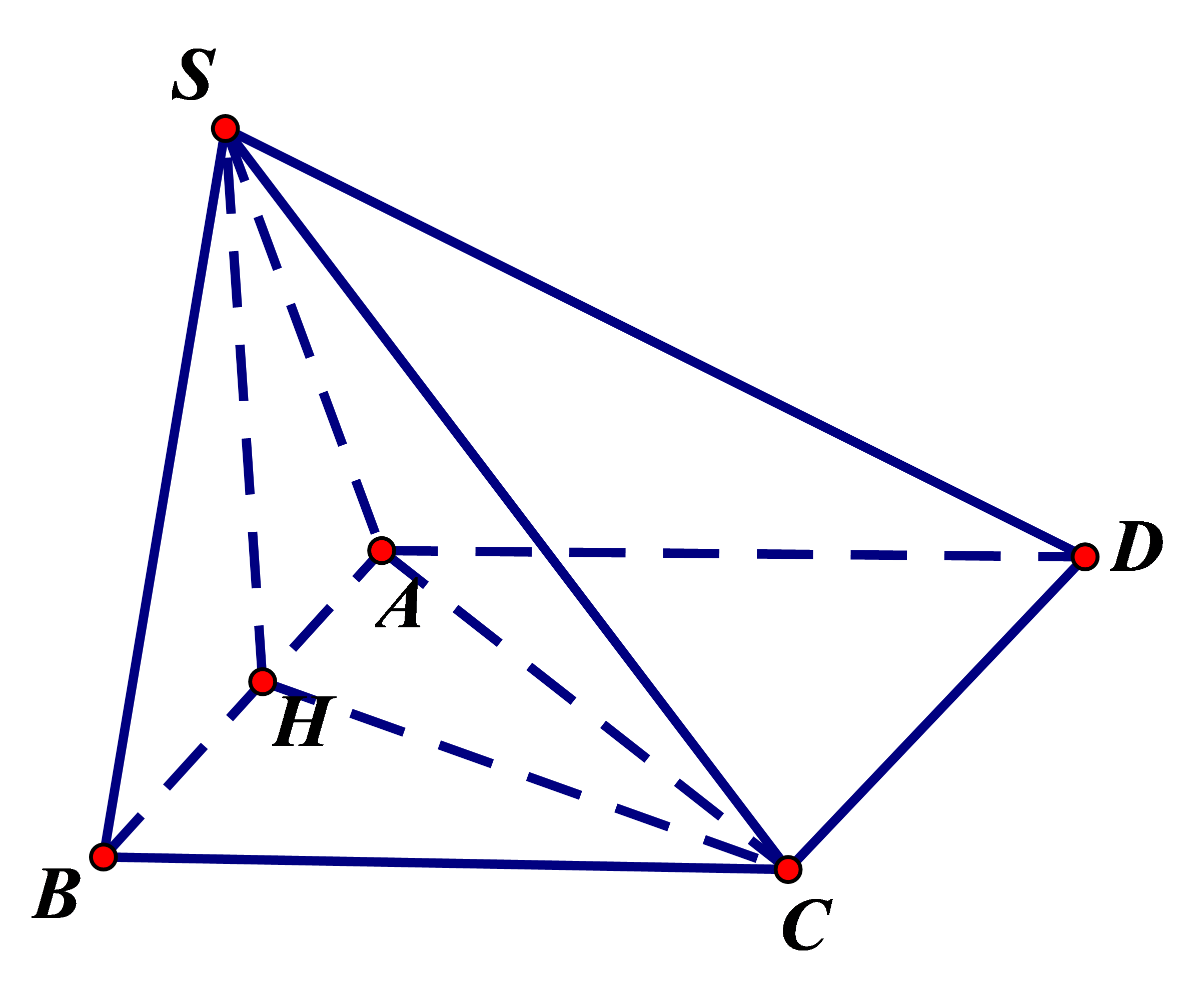
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc 600. Tính khoảng cách d từ điểm D đến mặt phẳng (SBC)
Hình vẽ minh họa
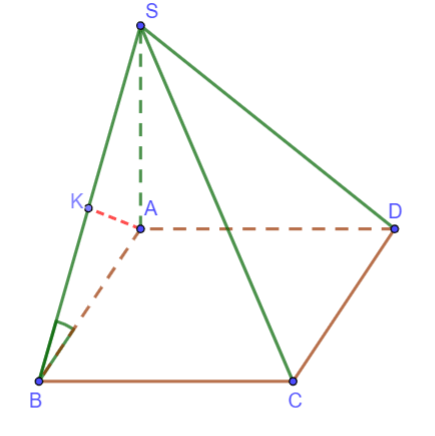
Ta có:
Ta có:
=>
Kẻ (1)
Ta có:
Từ (1) và (2) =>