Đề kiểm tra 15 phút Toán 11 Chương 8 Chân trời sáng tạo

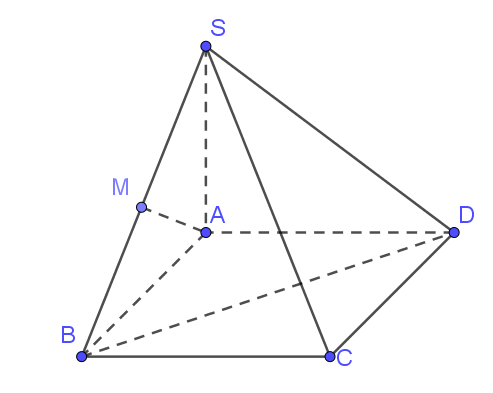
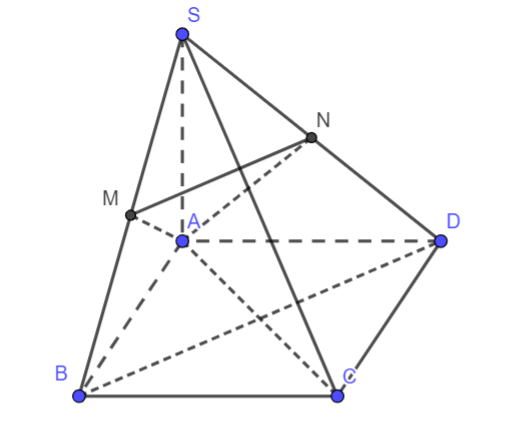
Hình ảnh minh họa:

Dễ dàng xác định giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d đi qua S và song song với AB.

Trong mặt phẳng (SAB) có SH ⊥ AB => SH ⊥ d.

Ta có:

=> d ⊥ SK. Từ đó suy ra ((SAB), (SCD)) = (SH, SK) =

Trong tam giác vuông SHK ta có:

Hình vẽ minh họa

Ta có: lần lượt là tâm các hình bình hành và

=> lần lượt là trung điểm của các cạnh

là đường trung bình tam giác

Vì đáy ABCD là hình thoi

Ta có:

Hình vẽ minh họa

Gọi I là trung điểm của AD

Tam giác SAD cân tại S suy ra

Ta có

Suy ra SI là đường cao của hình chóp

Theo giả thiết

Vì

Gọi H là hình chiếu vuông góc của I lên SD

Mặt khác . Ta có:

Xét tam giác SID vuông tại I có:

Hình vẽ minh họa:

Từ giả thiết suy ra tam giác ABD đều cạnh a.

Gọi H là hình chiếu của S trên mặt phẳng (ABCD).

Do SA = SB = SD nên suy ra H cách đều các đỉnh của tam giác ABD hay H là tâm của tam giác đều ABD.

Suy ra:

Vì ABCD là hình thoi nên HI ⊥ BD.

Tam giác SBD cân tại S nên SI ⊥ BD

=> ((SBD), (ABCD)) = (SI, AI) =

Trong tam vuông SHI ta có:

Gọi M, N lần lượt là trung điểm của CD, AB, ∆ACD và ∆BCD cân

=> AM ⊥ CD, BM ⊥ CD. Ta có:

=> AM ⊥ BM

Và ta dễ dàng chứng minh được ∆ACD = ∆BCD (c – c - c)

=> AM = BM => ∆ABM vuông cân tại M

=> MN ⊥ AB

Đặt CD = x

Áp dụng định lý Py-ta-go ta có:

Xét ∆ABM vuông cân tại M

Áp dụng định lý Py-ta-go ta có:

Xét ∆CDN vuông cân tại N

Ta có: 

Từ A kẻ =>

Hình vẽ minh họa:

Kẻ Mk // SO

Theo bài ra ta có: SO ⊥ (ABCD) => MK ⊥ (ABCD)

=>

Ta có:

Xét tam giác CNK có:

Xét tam giác MNK vuông ta có:

Hình vẽ minh họa:

Gọi N là trung điểm của BC, G là trọng tâm tam giác ABC.

Dựng hình chữ nhật AND

Kẻ GI // BC (I ∈ BD), GH ⊥ A’I (H ∈ A’I)

Ta có: C’N // (A’MB) (do C’N // MB)

=> d(C’, (A’BM)) = d(N, (A’BM))

Mà GN // (A’BM) (do GN // A’M)

=> d(N, (A’BM)) = d(G, (A’BM))

=> d(C’, (A’BM)) = d(G,(A’BM))

Ta có: BD // AN, AN // A’M => BD // A’M => A’, M, B, D đồng phẳng.

BD ⊥ GI (do ANBD là hình chữ nhật)

BD ⊥ A’G (do A’G ⊥ (ABC))

=> BD ⊥ (A’GI) => BD ⊥ GH

Mà A’I ⊥ GH => GH ⊥ (A’MB) => d(G, (A’BM)) = GH

Tính GH: ∆ABC đều, cạnh a

=>

Xét tam giác AA’G vuông tại G

=>

Ta lại có: GNBI là hình chữ nhật =>

Xét tam giác A’GI vuông tại G có GH ⊥ A’I

=>

Suy ra

Hình vẽ minh họa:

Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).

Do đó góc giữa SC và mặt phẳng (ABCD) là góc giữa SC và AC.

Hình vẽ minh họa

Ta có: nên SA là đường cao của hình chóp

Thể tích khối chóp là

Hình vẽ minh họa

Ta có:

Hình chiếu của SB lên mặt phẳng (SAC) là SO.

Vậy

Hình vẽ minh họa

Ta có tam giác SAC cân tại S và SO là đường trung tuyến cũng đồng thời là đường cao

=>

Trong tam giác SOA thì AC và SA không thể vuông tại A

Vậy khẳng định sai là: .

Hình vẽ minh họa:

Do I là trung điểm của SC và O là trung điểm AC nên IO ∥ SA. Do SA ⊥ (ABCD) nên IO ⊥ (ABCD), hay khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng IO

Hình vẽ minh họa

Từ giả thiết ta có: (do IJ là đường trung bình tam giác SAB)

Mặt khác ta lại có tam giác SAB đều nên

Xét vuông cân tại A, ta có:

Góc giữa 2 đường thẳng BA và BD bằng , suy ra

Xét vuông cân tại A, ta có:

Vì là trung điểm của SB nên:

Ta có:

(Do , nên )

Do đó: 

Vậy góc giữa AM bằng BD bằng 

Hình vẽ minh họa:

Ta có: SA ⊥ (ABCD) => SA ⊥ BC

Mà AB ⊥ BC => BC ⊥ (SAB)

=> BC ⊥ AE

Mà AM nằm trong mặt phẳng (SAB)

Xét tam giác SAB có:

AM ⊥ SB

Mà BC ⊥ AM => AM ⊥ (SBC) => AM ⊥ SC

Chứng minh tương tự ta được: AN ⊥ SC

=> SC ⊥ (AMN)

Hình vẽ minh họa

Gọi H là trung điểm của AB

Tam giác SAB cân tại S nên

Ta có:

Vậy SH là đường cao của hình chóp

Xét tam giác AHS vuông tại H ta có:

Vậy thể tích hình chóp là:

Trong không gian, tập hợp các điểm M cách đều hai điểm A và B là mặt phẳng trung trực của đoạn thẳng AB.

Hình vẽ minh họa:

Ta có:

Lại có:

=>