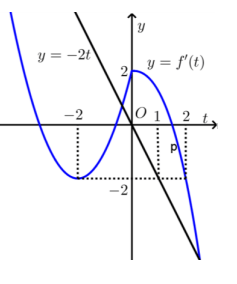
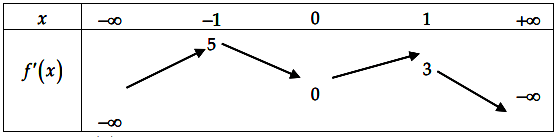
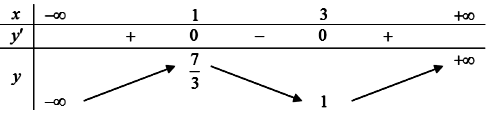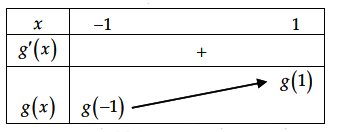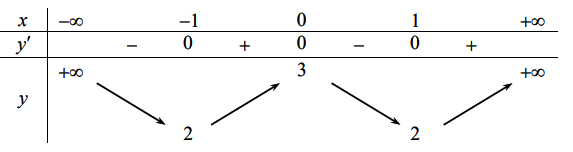Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ:
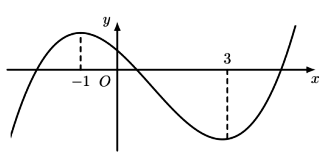
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số ![]() có 3 điểm cực trị. Tổng các phần tử của S là:
có 3 điểm cực trị. Tổng các phần tử của S là:
Xét hàm số có đạo hàm
Để hàm số có 3 điểm cực trị thì
Vậy tổng các phần tử của S là 2