Cho hình chóp tam giác đều ![]() . Mặt bên
. Mặt bên ![]() là tam giác gì?
là tam giác gì?
Hình chóp tam giác đều có các mặt bên là các tam giác cân.
Cho hình chóp tam giác đều ![]() . Mặt bên
. Mặt bên ![]() là tam giác gì?
là tam giác gì?
Hình chóp tam giác đều có các mặt bên là các tam giác cân.
Khối đa diện nào sau đây có số mặt nhỏ nhất?
Khối tứ diện đều có 4 mặt là 4 tam giác đều.
Khối chóp tứ giác có 5 mặt: 4 mặt xung quanh là các tam giác cân, mặt đáy là hình vuông.
Khối lập phương có 6 mặt tất cả, mỗi mặt đều là các hình vuông
Khối 12 mặt đều có 12 mặt tất cả, mỗi mặt là 1 hình ngũ giác đều.
Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình nào trong các hình sau đây?
Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình bát diện:

Trong các hình dưới đây hình nào không phải khối đa diện lồi?
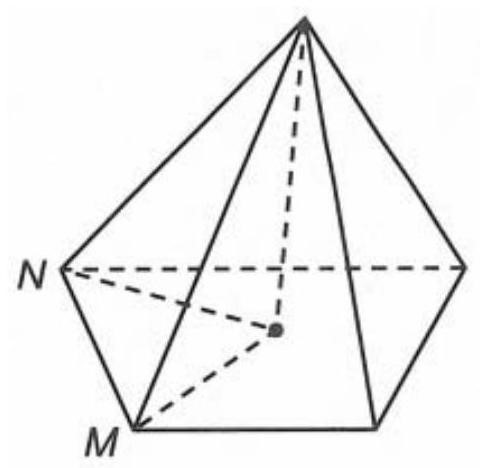
Đường nối đoạn MN không thuộc khối hình 4 nên hình 4 không phải khối đa diện lồi.
Mệnh đề nào sau đây đúng?
Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau:
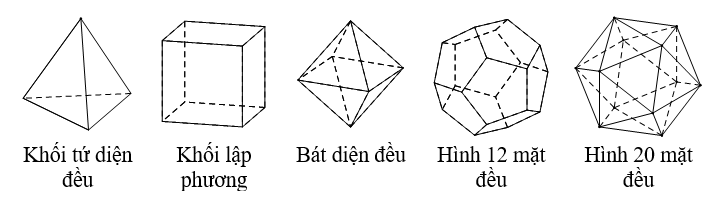
- Khối lập phương có 6 mặt.
"Mọi khối đa diện đều có số mặt là những số chia hết cho 4"
Sai.
- Khối lập phương và khối bát diện đều có cùng số cạnh là 12. Đúng
- Khối tứ diện đều không có tâm đối xứng.
"Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng": Sai.
- Khối 12 mặt đều có 20 đỉnh. Khối 20 mặt đều có 12 đỉnh.
"Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh": Sai
Trung điểm các cạnh của một tứ diện đều tạo thành?
Trung điểm các cạnh của một tứ diện đều tạo thành các đỉnh của một hình bát diện đều:

Khối lăng trụ ngũ giác có bao nhiêu cạnh?
Khối lăng trụ ngũ giác có số cạnh của một mặt đáy là 5 cạnh, số cạnh bên là 5 cạnh
Số cạnh của khối lăng trụ ngũ giác là: 2.5 + 5 =15 cạnh.
Cho lăng trụ đứng ![]() có đáy
có đáy ![]() là tam giác vuông tại
là tam giác vuông tại ![]() và
và ![]() . Cạnh
. Cạnh ![]() tạo với mặt đáy
tạo với mặt đáy ![]() góc
góc ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ đã cho.
của khối lăng trụ đã cho.
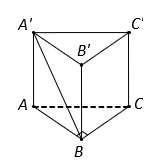
Vì là lăng trụ đứng nên
, suy ra hình chiếu vuông góc của
trên mặt đáy
là
.
Do đó .
Tam giác vuông , ta có
Diện tích tam giác là
Vậy .
Cho hình chóp ![]() có tam giác
có tam giác ![]() là tam giác vuông cân tại S,
là tam giác vuông cân tại S, ![]() và khoảng cách từ A đến mặt phẳng
và khoảng cách từ A đến mặt phẳng ![]() bằng
bằng ![]() . Tính theo a thể tích V của khối chóp
. Tính theo a thể tích V của khối chóp ![]() .
.
Ta chọn (SBC) làm mặt đáy suy ra chiều cao khối chóp là
Tam giác SBC vuông cân tại S nên
Vậy thể tích khối chóp
Tính thể tích ![]() của khối lăng trụ
của khối lăng trụ ![]() biết thể tích khối chóp
biết thể tích khối chóp ![]() bằng
bằng ![]()
Ta có thể tích khối chóp:
Suy ra:
Cho hình chóp 22 cạnh. Tính số mặt của hình chóp đó?
Gọi số cạnh đáy là với
Đáy của chóp là
– giác.
Ứng với mỗi đỉnh của đáy của 1 cạnh nối đỉnh của hình chóp với đỉnh của chóp.
Suy ra hình chóp có tổng số cạnh là .
Theo đề bài, hình chóp có 22 cạnh nên ta được (TMĐK)
Do đó, hình chóp có đáy là 11 – giác.
Do đó chóp có 11 mặt bên cộng 1 đáy.
Vậy hình chóp có tổng 12 mặt.
Tính thể tích ![]() của khối lăng trụ tam giác đều có tất cả các cạnh bằng
của khối lăng trụ tam giác đều có tất cả các cạnh bằng ![]() ?
?
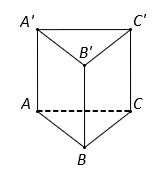
Xét khối lăng trụ tam giác đều có tất cả các cạnh bằng
.
Mỗi khối đa diện đều mà mỗi đỉnh của nó đều là đỉnh chung của ba mặt thì số đỉnh Đ và số cạnh C của các khối đa diện đó luôn thỏa mãn?
Do mỗi đỉnh là đỉnh chung của đúng ba mặt nên suy ra số cạnh của khối đa diện là 3Đ.
Mặt khác, mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức .
Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?
Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt phẳng đối xứng bao gồm:
- Hai mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.
- Một mặt phẳng là mặt phẳng trung trực của cạnh bên.
Cho các hình sau: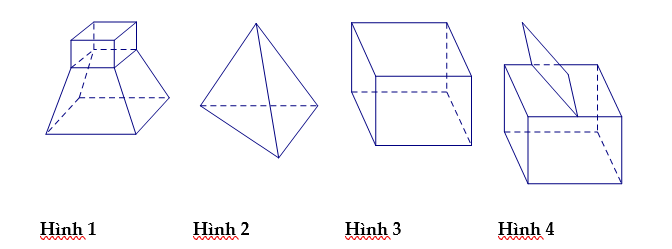
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là:
Áp dụng định nghĩa hình đa diện, ta có:
“Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:
TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.
TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.
TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt sao cho S0 trùng với S, Sn trùng với S’ và bất kì hai mặt
nào
cũng đều có một cạnh chung.
Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”
Tính thể tích ![]() của khối lăng trụ tam giác đều có cạnh đáy bằng
của khối lăng trụ tam giác đều có cạnh đáy bằng ![]() và tổng diện tích các mặt bên bằng
và tổng diện tích các mặt bên bằng ![]()

Xét khối lăng trụ có đáy
là tam giác đều và
.
Diện tích xung quanh lăng trụ là
Diện tích tam giác là
.
Vậy thể tích khối lăng trụ là .
Cho tứ diện ![]() có thể tích bằng
có thể tích bằng ![]() và
và ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() . Tính thể tích
. Tính thể tích ![]() của khối chóp .
của khối chóp .![]()
4 || Bốn || bốn
Cho tứ diện có thể tích bằng
và
là trọng tâm của tam giác
. Tính thể tích
của khối chóp .
4 || Bốn || bốn
Vì là trọng tâm của tam giác
nên
.
Suy ra
Trong các mệnh đề sau, mệnh đề nào saì?
Áp dụng khái niệm đa diện lồi, ta thấy hình hộp, tứ diện, lập phương đều là các đa diện lồi. Xét đáp án còn lại, ta có:
- Hai tứ diện đều ghép vào nhau có thể không tạo thành một hình đa diện lồi.
- Hai tứ diện (đều là các đa diện lồi) nhưng khi ghép với nhau có thể không tạo thành một hình đa diện lồi.
Hình đa diện nào dưới đây không có tâm đối xứng?
Mọi hình chóp đều không có tâm đối xứng (tứ diện đều, hình chóp tứ giác đều,….)
Hình lăng trụ tam giác cũng không có tâm đối xứng.
Mọi hình hộp chữ nhật, hình lập phương đều có tâm đối xứng
Bát diện đều cũng có tâm đối xứng.
Trong các mệnh đề sau, mệnh đề nào sai?
Trong 5 loại khối đa diện đều không tồn tại khối chóp có đáy là tứ giác!
Cho hình chóp ![]() có thể tích bằng
có thể tích bằng ![]() , đáy
, đáy ![]() là hình vuông;
là hình vuông; ![]() và
và ![]() hợp với đáy một góc bằng
hợp với đáy một góc bằng ![]() . Mặt phẳng
. Mặt phẳng ![]() đi qua A và vuông góc với
đi qua A và vuông góc với ![]() , cắt các cạnh
, cắt các cạnh ![]() lần lượt tại
lần lượt tại ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() .
.
V/10 || V phần 10
Cho hình chóp có thể tích bằng
, đáy
là hình vuông;
và
hợp với đáy một góc bằng
. Mặt phẳng
đi qua A và vuông góc với
, cắt các cạnh
lần lượt tại
. Tính thể tích khối chóp
.
V/10 || V phần 10
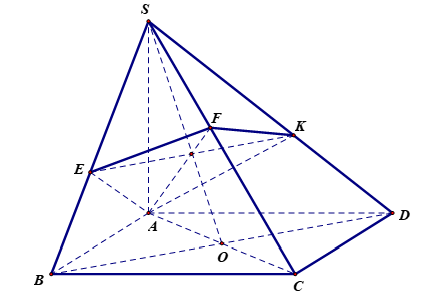
Ta có . Tương tự
nên
.
Mà (do
vuông tại A,
) nên ta có:
Xét tỉ số thể tích, ta được:
Tổng độ dài ![]() của tất cả các cạnh của khối mười hai mặt đều cạnh bằng 2
của tất cả các cạnh của khối mười hai mặt đều cạnh bằng 2
60 || sáu mươi || Sáu mươi
Tổng độ dài của tất cả các cạnh của khối mười hai mặt đều cạnh bằng 2
60 || sáu mươi || Sáu mươi
Khối mười hai mặt đều có tất cả 30 cạnh:

Suy ra ta có tổng độ dài tất cả các cạnh bằng .
Cho hình chóp ![]() có đáy
có đáy ![]() là hình chữ nhật có cạnh AB=a, BC =2a. Hai mặt bên
là hình chữ nhật có cạnh AB=a, BC =2a. Hai mặt bên ![]() và
và ![]() cùng vuông góc với mặt phẳng đáy
cùng vuông góc với mặt phẳng đáy ![]() . Tính theo a thể tích V của khối chóp
. Tính theo a thể tích V của khối chóp ![]()
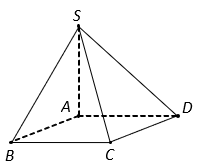
Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với (ABCD), suy ra . Do đó chiều cao khối chóp là
.
Diện tích hình chữ nhật ABCD là
Vậy thể tích khối chóp
Tổng các góc ở đỉnh của tất cả các mặt của khối đa diện đều loại ![]() là:
là:
Khối đa diện đều loại là khối hai mươi mặt đều:
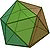
Gồm 20 mặt là các tam giác đều nên tổng các góc bằng:
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
Hình lăng trụ tam giác đều có 1 mặt phẳng đối xứng đi qua trung điểm của các cạnh bên (song song với đáy) và 3 mặt phẳng đối xứng vuông góc với đáy ( giao với 2 đáy theo các đường trung tuyến của tam giác đáy).
Vậy hình lăng trụ tam giác đều có mặt phẳng đối xứng (hình vẽ bên dưới).
Cho hình chóp ![]() có đáy ABC là tam giác vuông tại B và
có đáy ABC là tam giác vuông tại B và ![]() . Cạnh bên
. Cạnh bên ![]() và vuông góc với mặt phẳng đáy. Tính theo a thể tích V của khối chóp
và vuông góc với mặt phẳng đáy. Tính theo a thể tích V của khối chóp ![]() .
.
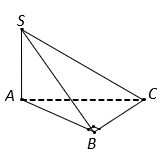
Diện tích tam giác vuông
Chiều cao khối chóp là .
Vậy thể tích khối chóp
Số cạnh của hình đa diện luôn luôn là một số tự nhiên
Có thể lấy tứ diện làm đại diện để xét với số đỉnh là 4, số cạnh là 6 và số mặt là 4.
Cho hình bát diện đều cạnh ![]() . Gọi
. Gọi ![]() là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?
là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?
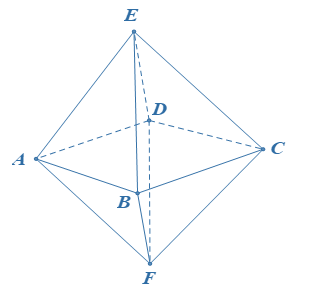
Hình bát diện đều là hình có tám mặt bằng nhau và mỗi mặt là một tam giác đều. Gọi là diện tích tam giác đều cạnh
Vậy diện tích S cần tính là: .
Chọn khẳng định đúng trong các khẳng định sau:
Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều:
Cho lăng trụ đứng ![]() có đáy
có đáy ![]() là hình thoi cạnh bằng 1,
là hình thoi cạnh bằng 1, ![]() . Góc giữa đường thẳng
. Góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ.
của khối lăng trụ.
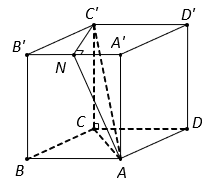
Hình thoi có
, suy ra
. Do đó tam giác
và
là các tam giác đều. Gọi N là trung điểm A'B' nên
Suy ra .
Tam giác vuông , có
Tam giác vuông , có
.
Diện tích hình thoi .
Vậy .
Cho hình hộp chữ nhật ![]() có
có ![]() , đường chéo
, đường chéo ![]() hợp với mặt đáy
hợp với mặt đáy ![]() một góc
một góc ![]() thỏa mãn
thỏa mãn ![]() . Tính theo
. Tính theo ![]() thể tích khối hộp đã cho.
thể tích khối hộp đã cho.
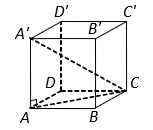
Ta có nên
.
Tam giác vuông , ta có
.
Tam giác vuông , ta có
.
Diện tích hình chữ nhật là
.
Vậy .
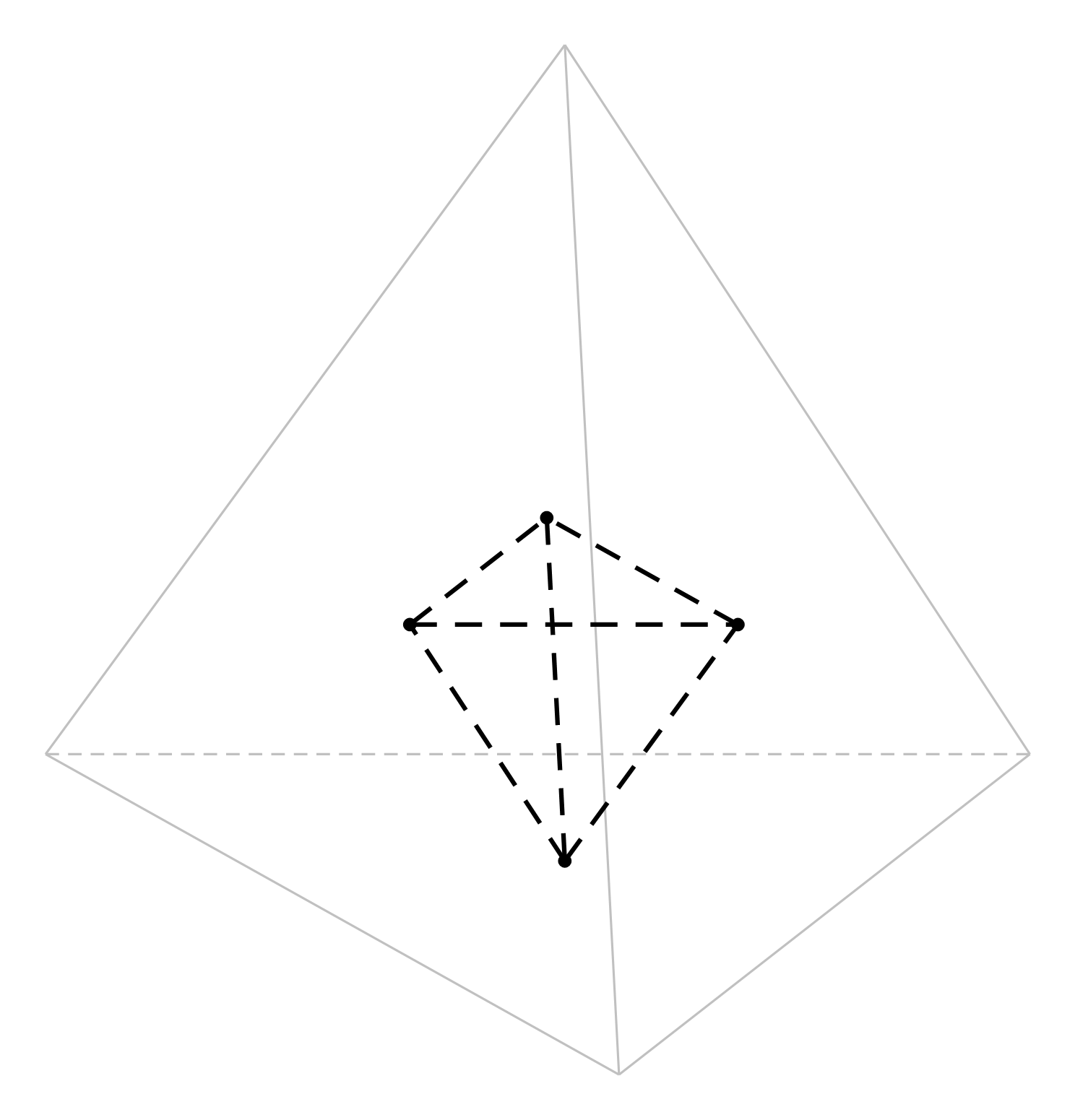
Tổng độ dài ![]() của tất cả các cạnh của một tứ diện đều cạnh
của tất cả các cạnh của một tứ diện đều cạnh ![]() .
.
Tứ diện đều có tất cả cạnh nên có tổng độ dài các cạnh là
Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có kích thước như trong hình vẽ.
 Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính ![]() , trong đó
, trong đó ![]() lần lượt là thể tích của mẫu lều cắm trại ở hình a, hình b. Giá trị của
lần lượt là thể tích của mẫu lều cắm trại ở hình a, hình b. Giá trị của ![]() bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
Đáp án: 961 dm3
Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có kích thước như trong hình vẽ.
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính
, trong đó
lần lượt là thể tích của mẫu lều cắm trại ở hình a, hình b. Giá trị của
bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
Đáp án: 961 dm3
Cả hai lều đều có dạng khối lăng trụ đứng ngũ giác.
Xét khối lăng trụ ở hình a. Chia mặt đáy thành hai phần bao gồm: hình chữ nhật có chiều rộng , chiều dài
; tam giác cân có cạnh đáy dài
, chiều cao
như hình dưới đây.
Diện tích mặt đáy của lăng trụ đó là:
Vậy thể tích của khối lăng trụ ngũ giác đó là:
.
Xét khối lăng trụ ở hình . Chia mặt đáy thành hai phần bao gồm: hình thang cân có đáy lớn đài
, đáy nhỏ dài
, chiều cao
tam giác cân có cạnh đáy dài
, chiều cao
như hình vẽ .
Diện tích mặt đáy của lăng trụ đó là:
Vậy thể tích của khối lăng trụ ngũ giác đó là:
Do đó .
Cho các hình khối sau:
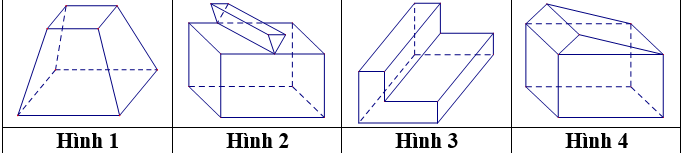
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là?
2 || Hai || hai
Cho các hình khối sau:

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là?
2 || Hai || hai
Có hai khối đa diện lồi là: Hình 1 & Hình 4
Cho tứ diện có thể tích bằng ![]() . Gọi
. Gọi ![]() là thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số
là thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số ![]() .
.
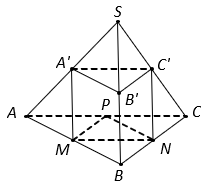
Xét khối tứ diện và các điểm được kí hiệu như hình vẽ trên, ta có:
Tương tự .
Do đó
.
Một hình đa diện có các mặt là những tam giác. Gọi M là tổng số mặt và C là tổng số cạnh của đa diện đó. Mệnh đề nào sau đây đúng.
Vì mỗi mặt là những tam giác nên có tổng số cạnh là 3M. Mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức 3M = 2C.
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị chục nghìn.

Đáp án: 4054 (chục nghìn)
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị chục nghìn.
Đáp án: 4054 (chục nghìn)
Hình vẽ minh họa
Mô hình hóa chân tháp của bài toán bằng khối chóp cụt tứ giác đều , với
lần lượt là tâm của hai đáy
và
.
Như vậy ta có:
là hình vuông cạnh 5 có diện tích
;
là hình vuông cạnh 2 có diện tích
;
Các cạnh bên có độ dài bằng 3;
vuông góc với (
) và (
.
Do ABCD là hình vuông nên , do đó tam giác ABC vuông tại B.
Áp dụng định lí Pythagore vào tam giác vuông tại
có:
Suy ra .
Do đó (do 0 là tâm hình vuông
).
Do là hình vuông nên
, do đó tam giác
vuông tại
.
Áp dụng định lí Pythagore trong tam giác vuông tại
có:
.
Suy ra .
Do đó (do
là tâm hình vuông
).
Dễ thấy: ;
.
Mà ( ) // (
.
Suy ra hay
là hình thang.
Xét hình thang , kẻ
.
Vì và
nên
.
Do đó (cùng vuông góc với AC).
Mà (do
)
Suy ra là hình bình hành.
Do đó: và
.
Suy ra .
Áp dụng định lí Pythagore trong tam giác vuông tại
do
có:
Suy ra .
Do đó .
Thể tích khối chóp cụt tứ giác đều với chiều cao
và diện tích hai đáy
,
là:
Như vậy ta có thể tích của chân tháp đã cho bằng .
Vi chân tháp được làm bằng bê tông tươi với giá tiền là 1470000 đồng nên số tiền để mua bê tông tươi làm chân tháp là:
(đồng)
Vậy số tiền để mua bê tông tươi làm chân tháp khoảng 40538432 đồng.
Cho các hình sau: 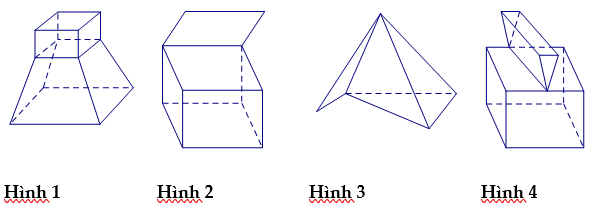
Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
Áp dụng định nghĩa hình đa diện, ta có:
“Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:
TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.
TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.
TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt sao cho trùng với trùng với S’ và bất kì hai mặt
nào
cũng đều có một cạnh chung.
Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”
Tổng các góc ở đỉnh của tất cả các mặt của khối đa diện đều loại ![]() là:
là:
Khối đa diện đều loại là khối lập phương, gồm 6 mặt là các hình vuông nên tổng các góc bằng:
Cho hình chóp ![]() có đáy là hình thang vuông tại A và B,
có đáy là hình thang vuông tại A và B, ![]() . Cạnh bên
. Cạnh bên ![]() và vuông góc với đáy. Tính thể tích khối chóp
và vuông góc với đáy. Tính thể tích khối chóp ![]() .
.
1
Cho hình chóp có đáy là hình thang vuông tại A và B,
. Cạnh bên
và vuông góc với đáy. Tính thể tích khối chóp
.
1
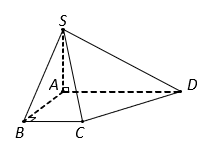
Diện tích hình thang ABCD là
Chiều cao khối chóp là .
Vậy thể tích khối chóp
