Tập hợp ![]() bằng tập hợp nào sau đây?
bằng tập hợp nào sau đây?
Xác định kết quả tập hợp bằng trục số như sau:
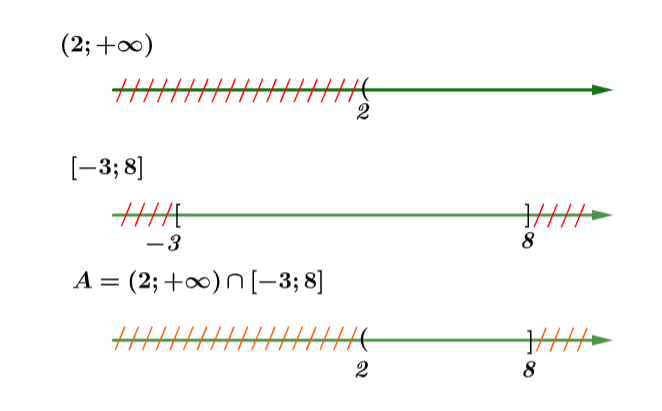
Vậy
Tập hợp ![]() bằng tập hợp nào sau đây?
bằng tập hợp nào sau đây?
Xác định kết quả tập hợp bằng trục số như sau:

Vậy
Tìm phát biểu là mệnh đề.
Ta có:
Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai của nó. Một mệnh đề không thể vừa đúng, vừa sai.
Suy ra “Hà Nội là thủ đô của Việt Nam.” là mệnh đề.
Cho mệnh đề P: “∆ABC cân tại A ⇔ AB = AC”. Chọn khẳng định đúng nhất trong các khẳng định sau?
Vì AB = AC nên suy ra ∆ABC cân tại A.
Vì ∆ABC cân tại A nên suy ra AB = AC.
Do đó đáp án đúng là “∆ABC cân tại A” là điều kiện cần và đủ để “AB = AC”.
Cho 2 mệnh đề: “Quyển vở này của Nam” và “Quyển vở này có 118 trang”.
Cho biết 2 mệnh đề trên đều đúng, tìm mệnh đề sai trong các mệnh đề sau:
Đặt “Quyển vở này của Nam”,
“Quyển vở này có 118 trang”
Theo đề bài, đúng,
đúng nên
sai,
sai.
Mệnh đề chỉ sai khi
đúng
sai.
Chọn đáp án Quyển vở này của Nam nên nó không có 118 trang.
Câu nào là mệnh đề toán học?
Mệnh đề toán học là: "2 là số tự nhiên"
Cho hai số thực x, y thoả mãn ![]() . Hãy tìm giá trị nhỏ nhất m và lớn nhất M của biểu thức
. Hãy tìm giá trị nhỏ nhất m và lớn nhất M của biểu thức ![]() .
.
Từ giả thiết suy ra và
,
chính là khoảng cách giữa
số
và
trên trục số.
nhỏ nhất khi
và
;
lớn nhất khi
và
.
Vậy .
Khi x là số lẻ, mệnh đề nào sau đây là mệnh đề sai:
Khi x là số lẻ => “x không chia hết cho 4” là mệnh đề đúng.
Khi x là số lẻ “x không chia hết cho 3” và “x chia hết cho 3” là một khẳng định nhưng không xác định được tính hoặc đúng hoặc sai tùy theo giá trị của x => Không phải mệnh đề.
Khi x là số lẻ “x chia hết cho 2” là mệnh đề sai.
Có bao nhiêu câu là mệnh đề trong các câu sau:
(1) Môn toán khó quá!
(2) Bạn có đói không?
(3) ![]() hoặc
hoặc ![]()
(4) ![]()
Câu (1) là câu cảm thán, câu (2) là câu nghi vấn nên không phải mệnh đề.
Các câu còn lại là mệnh đề.
Có
câu là mệnh đề.
Hãy liệt kê các phần tử của tập hợp ![]()
Ta có: không có nghiệm thực.
Khẳng định nào đúng trong các khẳng định sau:
Khẳng định đúng: "Nếu và
thì
"
Mệnh đề nào sau đây sai?
Mệnh đề đúng khi
đúng và
đúng.
là tam giác đều
là mệnh đề đúng.
là tam giác đều là mệnh đề sai
“
là tam giác đều
” là mệnh đề sai.
Chọn đáp án là tam giác đều
Cho tập hợp ![]() và
và ![]() Tập
Tập ![]() là:
là:
Xác định tập hợp ![]() bằng cách liệt kê các phần tử.
bằng cách liệt kê các phần tử.
Ta có: .
Cho hai tập hợp ![]() ,
, ![]() . Tìm tất cả các giá trị của tham số
. Tìm tất cả các giá trị của tham số ![]() để
để ![]() .
.
Ta có:
Do đó để
Cho hai tập hợp ![]() và
và ![]() với
với ![]() . Tìm a để
. Tìm a để ![]() là một khoảng?
là một khoảng?
Vì nên
và
, tức là A và B luôn là các khoảng.
Xét các trường hợp sau:
Nếu
Khi đó , đương nhiên là một khoảng.
Nếu
Nếu
Khi đó là một khoảng.
Nếu
Khi đó là một khoảng. Vậy các giá trị của a thỏa yêu cầu bài toán là
.
Có bao nhiêu câu là mệnh đề trong các câu sau:
(1) Chăm chỉ lên nhé!
(2) Số 20 chia hết cho 6.
(3) Số ![]() là số nguyên tố.
là số nguyên tố.
(4) Số ![]() là một số chẵn.
là một số chẵn.
Câu (1) là câu cảm thán nên không phải mệnh đề.
Các câu còn lại là mệnh đề.
Có
câu là mệnh đề.
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp ![]()
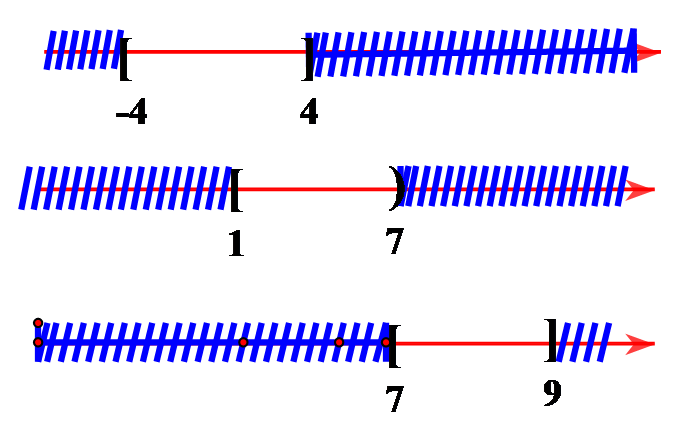
Vậy .
Điền vào chỗ trống: “Hiệu của tập hợp A và tập hợp B là ….”
Hiệu của tập hợp A và tập hợp B là tập hợp các phần tử thuộc A nhưng không thuộc B.
Trong các tập hợp sau, tập hợp nào bằng nhau:
=> ;
. Vậy tập hợp
không bằng tập hợp
.
=> . Vậy tập hợp
bằng tập hợp
. Đáp án đúng
=> ;
. Vậy tập hợp
không bằng tập hợp
.
=> ;
. Vậy tập hợp
không bằng tập hợp
.
Trong các mệnh đề sau, mệnh đề nào đúng?
Xét: ∃x ∈ R, x > x2. Với thì
.
Xét: ∀x ∈ R, . Sai. Tồn tại
thì
là mệnh đề sai.
Xét: ∀n ∈ N, n2 + 1 chia hết cho 3. . Sai. Vì tồn tại không chia hết cho 3.
Xét: ∃ a∈ Q, a2 = 2. . Sai. Vì không là số hữu tỉ.
Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:
Xét: Không có
thỏa mãn.
Cách viết tập hợp nào đúng trong các cách viết sau để xác định tập hợp A các ước dương của 12:
Các ước dương của 12 là: 1; 2; 3; 4; 6; 12
=> Cách viết tập hợp đúng là:
Phủ định của mệnh đề "![]() là số vô tỷ" là mệnh đề nào sau đây?
là số vô tỷ" là mệnh đề nào sau đây?
Phủ định của mệnh đề P là mệnh đề “không phải P".
Chọn đáp án không là số vô tỷ.
Cho ![]() Tập nào sau đây bằng tập
Tập nào sau đây bằng tập ![]()
Tập hợp gồm những phần tử vừa thuộc
vừa thuộc
Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp ![]() .
.
Ta có: .
Trong các mệnh đề sau, mệnh đề nào sai?
Mệnh đề: "Số 23 là hợp số" sai vì => 23 là số nguyên tố.
Cho hai tập hợp: X = ![]() là bội của
là bội của ![]() và
và ![]() và Y=
và Y= ![]() n là bội số của 12}
n là bội số của 12}
Trong các mệnh đề nào sau đây, mệnh đề nào là sai?
là bội của
và
là số tự nhiên chia hết cho
và
chia hết cho
Tập hợp các số tự nhiên chia hết cho
là bội của
chia hết cho
Tập hợp các số tự nhiên chia hết cho
đáp án sai là
và
Tập ![]() bằng tập nào sau đây?
bằng tập nào sau đây?
Ta có:
Trong các câu sau, câu nào không phải là mệnh đề toán học?
Đáp án “2x + y = −5” không phải mệnh đề vì nó không có tính đúng hoặc sai. Suy ra nó cũng không phải mệnh đề toán học.
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo ĐÚNG?
Nếu a chia hết cho 3 thì a chia hết cho 9 có mệnh đề đảo là Nếu a chia hết cho 9 thì a chia hết cho 3. Đây là mệnh đề đảo đúng.
Cho ![]() là tập hợp các số tự nhiên chẵn không lớn hơn
là tập hợp các số tự nhiên chẵn không lớn hơn ![]() ,
, ![]() . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?
Liệt kê các phần tử của tập hợp đã cho ta có kết luận đúng là:
Mệnh đề: " ![]() " khẳng định là
" khẳng định là
Mệnh đề: " " khẳng định là có ít nhất một số thực mà bình phương của nó lớn hơn 33.
Tìm đáp án không phải mệnh đề trong các câu sau.
Câu “Bộ phim quá hay!” là câu cảm thán nên không phải là mệnh đề.
Cho tập hợp A biểu thị trên trục số như hình dưới. Chọn khẳng định đúng:

Tập hợp A biểu thị trên trục số là nửa khoảng
Nếu A và B là tập hợp hữu hạn thì công thức nào sau đây đúng?
Nếu A và B là tập hợp hữu hạn thì
Cho biết ![]() là một phần tử của tập hợp
là một phần tử của tập hợp ![]() xét các mệnh đề sau:
xét các mệnh đề sau:
(I) ![]()
(II) ![]() .
.
(III) ![]()
(IV) ![]()
Trong các mệnh đề sau, mệnh đề nào là đúng:
I đúng.
II sai vì không có khái niệm tập hợp này thuộc tập hợp kia.
III sai vì phần tử thì không thể là con của
tập hợp.
IV đúng.
Xác định ![]() trong trường hợp
trong trường hợp ![]() {
{![]() ,
, ![]() và
và ![]() }, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12.
}, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12.
Liệt kê các phần tử ta có:
Vậy .
Cho tập hợp ![]() và
và ![]() Tập hợp
Tập hợp ![]() bằng tập nào sau đây?
bằng tập nào sau đây?
Tập hợp gồm những phần tử thuộc
nhưng không thuộc
.
Tìm mệnh đề phủ định của mệnh đề: “Vịt là một loài chim”.
Phủ định của mệnh đề P là mệnh đề “không phải P"
Chọn đáp án Vịt không phải là một loài chim.
Có bao nhiêu mệnh đề trong các câu sau?
Ở đây đẹp quá!
Phương trình ![]() vô nghiệm.
vô nghiệm.
16 không là số nguyên tố.
Số ![]() có lớn hơn
có lớn hơn ![]() hay không?
hay không?
Câu “Phương trình vô nghiệm.” và “16 không là số nguyên tố.” là mệnh đề.
