Tìm mệnh đề chứa biến.
“” là mệnh đề chứa biến.
Tìm mệnh đề chứa biến.
“” là mệnh đề chứa biến.
Khẳng định nào đúng trong các khẳng định sau:
Khẳng định đúng: "Nếu và
thì
"
Cho hai khoảng ![]() và
và ![]() . Khẳng định nào sau đây là sai?
. Khẳng định nào sau đây là sai?
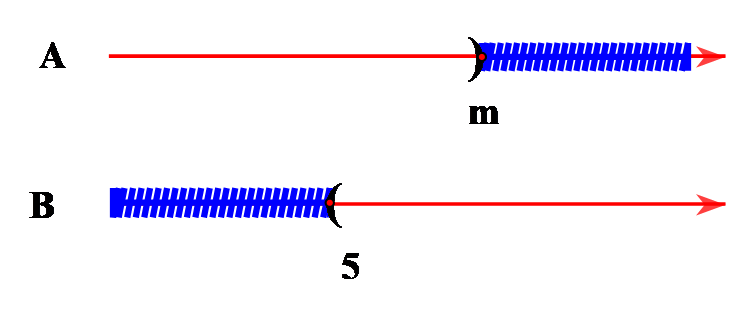
Vậy khi
Trong các mệnh đề sau mệnh đề nào:
Với nhưng
không chia hết cho
Chọn đáp án
Cho hai mệnh đề A: “∀ x ∈ R: ![]() ” và B: “∃ n ∈ Z:
” và B: “∃ n ∈ Z: ![]() ”. Xét tính đúng, sai của hai mệnh đề A và B.
”. Xét tính đúng, sai của hai mệnh đề A và B.
Với mệnh đề A, thay nên A sai.
Với mệnh đề B, thay nên B đúng.
Kí hiệu ![]() có nghĩa là gì?
có nghĩa là gì?
Cho hai tập hợp và
. Nếu
là tập con của
thì hiệu
gọi là phần bù của
trong
, kí hiệu
.
Hai mệnh đề sau là mệnh đề gì: “x chia hết cho 9” và “x chia hết cho 3”.
Nếu x chia hết cho 9 thì x chia hết cho 3.
Nếu x chia hết cho 3 thì x có thể không chia hết cho 9.
=> Hai mệnh đề “x chia hết cho 9” và “x chia hết cho 3” là mệnh đề kéo theo.
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp ![]()
Vậy .
Cho mệnh đề P: “∆ABC cân tại A ⇔ AB = AC”. Chọn khẳng định đúng nhất trong các khẳng định sau?
Vì AB = AC nên suy ra ∆ABC cân tại A.
Vì ∆ABC cân tại A nên suy ra AB = AC.
Do đó đáp án đúng là “∆ABC cân tại A” là điều kiện cần và đủ để “AB = AC”.
Trong định lí ta nói: "P là điều kiện cần để có Q". Khi đó P là gì của định lí?
Trong định lí ta nói: " là điều kiện cần để có
". Khi đó P là kết luận của định lí.
Cho hai số thực x, y thoả mãn ![]() . Hãy tìm giá trị nhỏ nhất m và lớn nhất M của biểu thức
. Hãy tìm giá trị nhỏ nhất m và lớn nhất M của biểu thức ![]() .
.
Từ giả thiết suy ra và
,
chính là khoảng cách giữa
số
và
trên trục số.
nhỏ nhất khi
và
;
lớn nhất khi
và
.
Vậy .
Cho A = {a, b}. Số tập con của A là:
Ta có: Số tập hợp con của tập có phần tử là
. Do đó số tập con của A là
.
Cho tập hợp A = {![]() , với
, với ![]() là số thực dương}. Tìm số lớn nhất của tập hợp A?
là số thực dương}. Tìm số lớn nhất của tập hợp A?
Ta có:
Đẳng thức xảy ra khi .
Vậy số nhỏ nhất là 3.
Kí hiệu nào sau đây dùng để viết đúng mệnh đề “![]() không phải là số hữu tỉ”
không phải là số hữu tỉ”
Ta có:
Cách biểu diễn nào sau đây đúng cho tập số [‒5; 5]
Ta có:
Dấu “[” và “]” kí hiệu cho nửa đoạn trên trục số.
Biểu diễn tập [‒5; 5] trên trục số đúng là:

Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều sai thì ta suy ra điều gì?
Ta có:
Mệnh đề đúng khi cả hai mệnh đề
và
cùng đúng hoặc cùng sai. (Hay
đúng khi cả hai mệnh đề
và
cùng đúng hoặc cùng sai).
Cho mệnh đề chứa biến ![]() chia hết cho 4” với
chia hết cho 4” với ![]() là số nguyên. Xét xem các mệnh đề
là số nguyên. Xét xem các mệnh đề ![]() và
và ![]() đúng hay sai?
đúng hay sai?
Thay và
vào
ta được các số
và
không chia hết cho
. Vậy
đúng và
sai.
Trong các câu sau, câu nào không phải là mệnh đề toán học?
Đáp án “2x + y = −5” không phải mệnh đề vì nó không có tính đúng hoặc sai. Suy ra nó cũng không phải mệnh đề toán học.
Tập hợp ![]() bằng tập hợp nào sau đây?
bằng tập hợp nào sau đây?
Ta có: .
Câu nào là mệnh đề toán học?
Mệnh đề toán học là: "2 là số tự nhiên"
Cho ba mệnh đề: ![]() “số
“số ![]() chia hết cho
chia hết cho ![]() và chia hết cho
và chia hết cho ![]() ”
”
Q: “ Số ![]() chia hết cho
chia hết cho ![]() ”
”
R: “ Số ![]() là số nguyên tố ”
là số nguyên tố ”
Hãy tìm mệnh đề sai trong các mệnh đề dưới đây:
đúng,
sai,
đúng.
đúng,
đúng nên
đúng,
đúng,
đúng nên
đúng,
đúng.
đúng,
đúng nên
đúng.
đúng,
đúng nên
đúng,
đúng,
sai nên
sai.
Chọn đáp án .
Cho ![]() là tập hợp các số tự nhiên chẵn không lớn hơn
là tập hợp các số tự nhiên chẵn không lớn hơn ![]() ,
, ![]() . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?
Liệt kê các phần tử của tập hợp đã cho ta có kết luận đúng là:
Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp ![]() .
.
Ta có: .
Cho mệnh đề: “Một tứ giác là hình thang cân khi và chỉ khi tứ giác đó có hai đường chéo bằng nhau”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?
Mệnh đề tương đương với mệnh đề đã cho là: Điều kiện cần và đủ để một tứ giác có hai đường chéo bằng nhau là tứ giác đó là một hình thang cân.
Cho tập hợp A = {![]() , với
, với ![]() là số thực dương}. Tìm số nhỏ nhất của tập hợp A?
là số thực dương}. Tìm số nhỏ nhất của tập hợp A?
Ta có:
Đẳng thức xảy ra khi .
Vậy số nhỏ nhất là
Hãy liệt kê các phần tử của tập hợp ![]()
Ta có: không có nghiệm thực.
Phát biểu lại mệnh đề "Nếu n = 2 thì ![]() là một hợp số".
là một hợp số".
Phát biểu lại mệnh đề trên: "n = 2 là điều kiện đủ để là một hợp số".
Cho ![]() Tập nào sau đây bằng tập
Tập nào sau đây bằng tập ![]()
Tập hợp gồm những phần tử vừa thuộc
vừa thuộc
Tập hợp ![]() bằng tập hợp nào sau đây?
bằng tập hợp nào sau đây?
Xác định kết quả tập hợp bằng hình vẽ như sau:
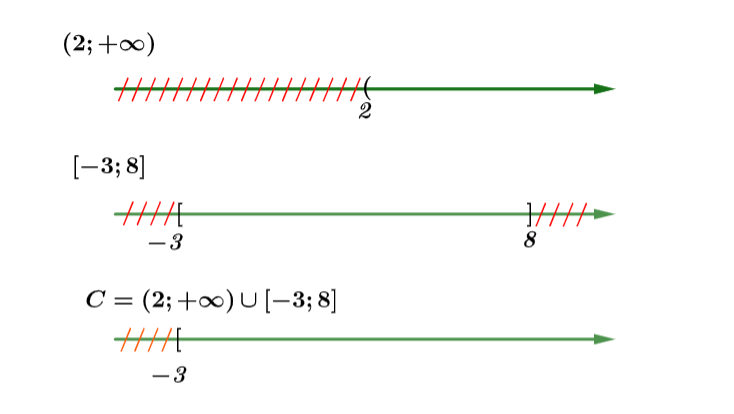
Vậy
Với giá trị nào của x thì mệnh đề chứa biến "![]() " là đúng?
" là đúng?
Thay vào 2 vế, ta được:
(đúng).
Cho tập hợp A biểu thị trên trục số như hình dưới. Chọn khẳng định đúng:

Tập hợp A biểu thị trên trục số là nửa khoảng
Tìm mệnh đề đúng.
Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Chọn Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
Tập ![]() bằng tập nào sau đây?
bằng tập nào sau đây?
Ta có:
Cho ![]()
![]() Tập hợp
Tập hợp ![]() bằng
bằng
Tập hợp gồm những phần tử thuộc
nhưng không thuộc
Cho mệnh đề P: “∀ x ∈ R: |x| ≥ 0” . Phủ định của mệnh đề P là:
Phủ định của mệnh đề P là: “∃ x ∈ R: |x| < 0”.
Tìm mệnh đề trong các câu sau.
Các câu “Hôm nay, trời đẹp quá!”, “Bạn ăn cơm chưa?”, “Mấy giờ rồi?” là các câu cảm thán hoặc nghi vấn nên không phải là mệnh đề.
Chọn đáp án Paris là thủ đô của Đức.
Cho tập ![]() Tập
Tập ![]() có bao nhiêu tập hợp con?
có bao nhiêu tập hợp con?
Tập có
phần tử
số tập con của
bằng:
.
Cho 2 mệnh đề: “Quyển vở này của Nam” và “Quyển vở này có 118 trang”.
Cho biết 2 mệnh đề trên đều đúng, tìm mệnh đề sai trong các mệnh đề sau:
Đặt “Quyển vở này của Nam”,
“Quyển vở này có 118 trang”
Theo đề bài, đúng,
đúng nên
sai,
sai.
Mệnh đề chỉ sai khi
đúng
sai.
Chọn đáp án Quyển vở này của Nam nên nó không có 118 trang.
Xác định tập hợp sau đây trên trục số: ![]() :
:
Xác định tập hợp trên trục số như sau:
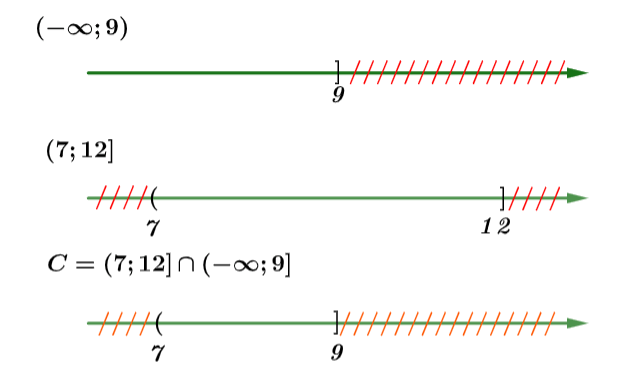
Cho biết ![]() là một phần tử của tập hợp
là một phần tử của tập hợp ![]() xét các mệnh đề sau:
xét các mệnh đề sau:
(I) ![]()
(II) ![]() .
.
(III) ![]()
(IV) ![]()
Trong các mệnh đề sau, mệnh đề nào là đúng:
I đúng.
II sai vì không có khái niệm tập hợp này thuộc tập hợp kia.
III sai vì phần tử thì không thể là con của
tập hợp.
IV đúng.
