Lớp 12 Toán 12 - Chân trời sáng tạo

Đề kiểm tra 45 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST

Mô tả thêm: Đề kiểm tra 45 phút bao gồm các kiến thức Chương 1. Ứng dụng đạo hàm để khảo sát hàm số được thay đổi liên tục giúp học sinh ôn tập kiến thức và kĩ năng giải bài tập Toán 12 CTST
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho hàm số y = \frac{{{x^2} + 3}}{{x - 1}}. Khẳng định nào sau đây đúng?

    Tập xác định D = \mathbb{R}\backslash \left\{ 1 ight\}

    \begin{matrix} y' = \dfrac{{{x^2} - 2x - 3}}{{{{\left( {x - 1} ight)}^2}}} \hfill \\ y' = 0 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - 1} \\ {x = 3} \end{array}} ight. \hfill \\ y'' = \frac{8}{{{{\left( {x - 1} ight)}^3}}} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {y''\left( { - 1} ight) = - 1 < 0} \\ {y''\left( 3 ight) = 1 > 0} \end{array}} ight. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{y_{CD}} = y\left( { - 1} ight) = - 2} \\ {{y_{CT}} = y\left( 3 ight) = 3} \end{array}} ight. \Rightarrow {y_{CD}} < {y_{CT}} \hfill \\ \end{matrix}

  • Câu 2: Nhận biết

    Cho hàm số f(x) có f'\left( x ight) = {\left( {x - 1} ight)^2}{\left( {x - 3} ight)^3}\left( {2x + 3} ight),\forall x \in \mathbb{R}. Số cực trị của hàm số đã cho là:

     Ta có: f’(x) đổi dấu khi qua các giá trị x = 3 và x = -3/2 nên hàm số có hai cực trị.

  • Câu 3: Nhận biết

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?

    Dựa vào bảng biến thiên ta có: \left\{ \begin{gathered} \mathop {\lim }\limits_{x \to - {2^ + }} f\left( x ight) = - \infty \hfill \\ \mathop {\lim }\limits_{x \to {0^ - }} f\left( x ight) = + \infty \hfill \\ \end{gathered} ight. nên đồ thị hàm số đã cho có hai tiệm cận đứng là x = - 2 và x = 0.

    \lim_{x ightarrow + \infty}y = 0 nên đồ thị hàm số đã cho có một tiệm cận ngang là y = 0

    Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.

  • Câu 4: Thông hiểu

    Cho hàm số y = f(x) có đồ thị như hình vẽ:

    Xác định khoảng đồng biến của hàm số g(x) = - 3f(x) + 2?

    Từ đồ thị hàm số y = f(x) ta có:

    f'(x) > 0 \Leftrightarrow \left\lbrack \begin{matrix} x < - 5 \\ x > 0 \\ \end{matrix} ight. và f'(x) < 0 \Leftrightarrow - 5 < x < 0

    Ta có: g'(x) = - 3f'(x)

    Khi đó: g'(x) > 0 \Leftrightarrow - 3f'(x) > 0 \Leftrightarrow f'(x) < 0 \Leftrightarrow - 5 < x < 0

    g'(x) < 0 \Leftrightarrow - 3f'(x) < 0 \Leftrightarrow f'(x) > 0 \Leftrightarrow \left\lbrack \begin{matrix} x < - 5 \\ x > 0 \\ \end{matrix} ight.

    Vậy hàm số g(x) = - 3f(x) + 2 đồng biến trên khoảng ( - 5;0).

  • Câu 5: Thông hiểu

    Có bao nhiêu giá trị nguyên của tham số m để hàm số y = \frac{1}{3}x^{3} - mx^{2} + (5m - 4)x - 1 không có điểm cực trị?

    Ta có: y' = x^{2} - 2mx + 5m - 4

    Hàm số đã cho không có cực trị khi và chỉ khi y' = 0 vô nghiệm hoặc có nghiệm kép.

    \Leftrightarrow \Delta' \leq 0 \Leftrightarrow m^{2} - 5m + 4 \leq 0 \Leftrightarrow m \in \lbrack 1;4brack

    Vì m\mathbb{\in Z \Rightarrow}m \in \left\{ 1;2;3;4 ight\}

    Vậy có bốn giá trị của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 6: Vận dụng cao

    Cho hàm số y = \left| x^{3} - (2m +1)x^{2} + mx + m ight| với m là tham số. Giả sử S là tập hợp tất cả các giá trị nguyên của m \in \lbrack -2021;2021brack sao cho đồ thị của hàm số có 5 điểm cực trị. Tính tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \left| x^{3} - (2m +1)x^{2} + mx + m ight| với m là tham số. Giả sử S là tập hợp tất cả các giá trị nguyên của m \in \lbrack -2021;2021brack sao cho đồ thị của hàm số có 5 điểm cực trị. Tính tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 7: Vận dụng cao

    Cho hàm số f(x) liên tục trên khoảng (0; +∞) thỏa mãn 3x.f\left( x ight) - {x^2}.f'\left( x ight) = 2{f^2}\left( x ight), với f(x) ≠ 0 với ∀x ∈ (0; +∞) và f\left( 1 ight) = \frac{1}{3}. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính tổng M + m.

    Ta có:

    \begin{matrix} 3x.f\left( x ight) - {x^2}.f'\left( x ight) = 2{f^2}\left( x ight) \hfill \\ \Rightarrow 3{x^2}f\left( x ight) - {x^3}f'\left( x ight) = 2x{f^2}\left( x ight) \hfill \\ \Rightarrow \dfrac{{3{x^2}f\left( x ight) - {x^3}f'\left( x ight)}}{{{f^2}\left( x ight)}} = 2x \hfill \\ \Rightarrow \left( {\dfrac{{{x^3}}}{{f\left( x ight)}}} ight)' = 2x \Rightarrow \dfrac{{{x^3}}}{{f\left( x ight)}} = {x^2} + C \hfill \\ \end{matrix}

    Thay x = 1 vào ta có: \left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{{f\left( 1 ight)}} = 1 + C} \\ {f\left( 1 ight) = \dfrac{1}{3}} \end{array}} ight. \Rightarrow C = 2

    \begin{matrix} \Rightarrow f\left( x ight) = \dfrac{{{x^3}}}{{{x^2} + 2}} \hfill \\ f'\left( x ight) = \dfrac{{{x^4} + 6{x^2}}}{{{{\left( {{x^2} + 2} ight)}^2}}} \hfill \\ f'\left( x ight) = 0 \Rightarrow x = 0 \hfill \\ \end{matrix}

    Ta có bảng biến thiên

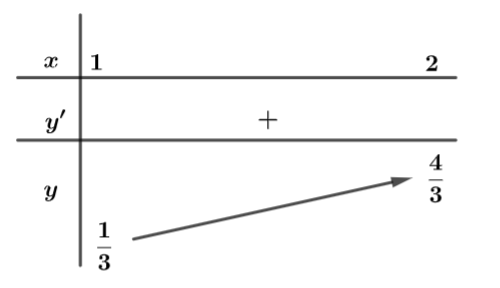
    Tính tổng GTLN và GTNN của hàm số

    Khi đó f(x) đồng biến trên [1; 2]

    => \left\{ {\begin{array}{*{20}{c}} {m = f\left( 1 ight) = \dfrac{1}{3}} \\ {M = f\left( 2 ight) = \dfrac{4}{3}} \end{array}} ight. \Rightarrow m + M = \dfrac{5}{3}

  • Câu 8: Vận dụng

    Cho hàm số y = \frac{x + 1}{\sqrt{ax^{2}+ 1}} có đồ thị (C). Tìm giá trị a để đồ thị hàm số có đường tiệm cận và đường tiệm cận đó cách đường tiếp tuyến của (C) một khoảng bằng \sqrt{2} - 1?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \frac{x + 1}{\sqrt{ax^{2}+ 1}} có đồ thị (C). Tìm giá trị a để đồ thị hàm số có đường tiệm cận và đường tiệm cận đó cách đường tiếp tuyến của (C) một khoảng bằng \sqrt{2} - 1?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 9: Nhận biết

    Tìm giá trị lớn nhất của hàm số y = f(x) = x4 – 2x2 + 1 trên đoạn [0; 2].

    Xét hàm số f(x) = x4 – 2x2 + 1 trên [0; 2] có:

    f’(x) = 4x3 – 4x

    f’(x) = 0 => \left\{ {\begin{array}{*{20}{c}}{x \in \left[ {0;2} ight]} \\ {4{x^3} - 4x = 0} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 1} \end{array}} ight.

    Tính f(0) = 1; f(1) = 0; f(2) = 9

    Vậy \mathop {\max }\limits_{\left[ {0;2} ight]} f\left( x ight) = f\left( 2 ight) = 9

  • Câu 10: Nhận biết

    Tìm hàm số luôn đồng biến trên từng khoảng xác định?

    Xét hàm số y = \frac{- x - 8}{x + 3}

    Tập xác định D\mathbb{= R}\backslash\left\{ - 3 ight\}. Ta có: y' = \frac{5}{\left( x + 3^{2} ight)} > 0;\forall x eq 3

    Vậy hàm số đồng biến trên các khoảng ( - \infty; - 3),( - 3; + \infty).

  • Câu 11: Vận dụng

    Biết hàm số y = (x - 1)(x + 1)\left(x^{2} - 7 ight) cắt trục hoành tại 4 điểm phân biệt có hoành độ là x_{1};x_{2};x_{3};x_{4}. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để \frac{1}{1 - x_{1}} + \frac{1}{1 - x_{2}} +\frac{1}{1 - x_{3}} + \frac{1}{1 - x_{4}} > 1?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Biết hàm số y = (x - 1)(x + 1)\left(x^{2} - 7 ight) cắt trục hoành tại 4 điểm phân biệt có hoành độ là x_{1};x_{2};x_{3};x_{4}. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để \frac{1}{1 - x_{1}} + \frac{1}{1 - x_{2}} +\frac{1}{1 - x_{3}} + \frac{1}{1 - x_{4}} > 1?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 12: Nhận biết

    Cho hàm số y = f(x) có đồ thị như hình vẽ:

    Đồ thị hàm số y = f(x) có mấy điểm cực trị?

    Từ đồ thị suy ra đồ thị có điểm một điểm cực tiểu và một điểm cực đại.

  • Câu 13: Thông hiểu

    Giá trị thực của tham số m để hàm số y = - x^{3} + mx^{2} + \left( m^{2} - 12 ight)x + 2 đạt cực tiểu tại điểm x = - 1 thuộc khoảng nào sau đây?

    Tập xác định D\mathbb{= R}

    Ta có: \left\{ \begin{matrix} y' = - 3x^{2} + 2mx + m^{2} - 12 \\ y'' = - 6x + 2m \\ \end{matrix} ight.

    Để hàm số đạt cực tiểu tại x = - 1 thì

    \left\{ \begin{matrix} y'(1) = 0 \\ y''(1) > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} - 2m - 15 = 0 \\ m > - 3 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} m = 5(tm) \\ m = - 3(ktm) \\ \end{matrix} ight.\ \\ m > - 3 \\ \end{matrix} ight.\ \Leftrightarrow m = 5

    Vậy m = 5 \in (3;6).

  • Câu 14: Nhận biết

    Cho hàm số y = \frac{2x - 1}{x + 3}. Khẳng định nào sau đây đúng?

    Tập xác định D\mathbb{= R}\backslash\left\{ - 3 ight\}

    Ta có: y' = \frac{7}{(x + 3)^{2}} > 0;\forall x \in D

    Suy ra hàm số đồng biến trên mỗi khoảng ( - \infty;3) và (3; + \infty).

  • Câu 15: Vận dụng

    Cho hàm số y = f(x) liên tục trên tập số thực và có bảng biến thiên như sau:

    Đặt g(x) = \left| f(x + 1) + might| với m là tham số. Tìm điều kiện của tham số m để hàm số y = g(x) có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) liên tục trên tập số thực và có bảng biến thiên như sau:

    Đặt g(x) = \left| f(x + 1) + might| với m là tham số. Tìm điều kiện của tham số m để hàm số y = g(x) có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 16: Nhận biết

    Chọn hàm số tương ứng với bảng biến thiên sau?

    Từ bảng biến thiên ta suy ra đồ thị hàm số bậc 4 trùng phương có hệ số a < 0 nên hàm số cần tìm là y = - x^{4} + 2x^{2} + 1.

  • Câu 17: Nhận biết

    Cho hàm số y = f(x) có đồ thị như sau:

    Hỏi số nghiệm của phương trình 2f(x) - 1 = 0 bằng bao nhiêu?

    Ta có: 2f(x) - 1 = 0 \Leftrightarrow f(x) = \frac{1}{2}

    Lại có đường thẳng y = \frac{1}{2} nằm phía trên gốc tọa độ; song song với trục Ox và cắt đồ thị hàm số y = f(x) tại 4 điểm nên phương trình 2f(x) - 1 = 0 có hai nghiệm.

  • Câu 18: Nhận biết

    Cho hàm số y = f(x) có đạo hàm trên \mathbb{R} là f'(x) = x^{2}(x - 1). Hàm số y = f(x) đồng biến trên khoảng nào sau đây?

    Ta có: f'(x) = 0 \Leftrightarrow x^{2}(x - 1) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight.. Lập bảng xét dấu như sau:

    Suy ra hàm số y = f(x) đồng biến trên khoảng (1; + \infty)

  • Câu 19: Thông hiểu

    Cho hàm số y = f(x) có bảng biến thiên như hình vẽ:

    a) Phương trình f(x) = 0 có 3 nghiệm. Đúng||Sai

    b) Phương trình f(x) = 2 có 1 nghiệm. Đúng||Sai

    c) Phương trình f(x) − 4 = 0 vô nghiệm. Sai||Đúng

    d) Phương trình f(x) + 3 = 0 có 2 nghiệm. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) có bảng biến thiên như hình vẽ:

    a) Phương trình f(x) = 0 có 3 nghiệm. Đúng||Sai

    b) Phương trình f(x) = 2 có 1 nghiệm. Đúng||Sai

    c) Phương trình f(x) − 4 = 0 vô nghiệm. Sai||Đúng

    d) Phương trình f(x) + 3 = 0 có 2 nghiệm. Đúng||Sai

    a) Ta có f(x) = 0.

    Dựa vào bảng biến thiên, ta có phương trình f(x) = 0 có 3 nghiệm.

    b) Ta có f(x) = 2

    Dựa vào bảng biến thiên, ta có phương trình f(x) = 2 có 1 nghiệm.

    c) Ta có f(x) + 4 = 0 ⇔ f(x) = −4.

    Dựa vào bảng biến thiên, ta có phương trình f(x) = −4 có 1 nghiệm.

    d) Ta cóf(x) + 3 = 0 ⇔ f(x) = −3.

    Dựa vào bảng biến thiên, ta có phương trình f(x) = −3 có 2 nghiệm.

  • Câu 20: Vận dụng

    Tìm giá trị thực của tham số m để hàm số f(x) = -x3 – 3x2 + m có giá trị nhỏ nhất trên đoạn [-1; 1] bằng 0.

    Xét hàm số f(x) = -x3 – 3x2 + m trên đoạn [-1; 1] ta có:

    f’(x) = -3x2 – 6x

    f’(x) = 0 => \left\{ {\begin{array}{*{20}{c}} { - 1 \leqslant x \leqslant 1} \\ { - 3{x^2} - 6x = 0} \end{array}} ight. \Leftrightarrow x = 0

    Ta tính được

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {f\left( { - 1} ight) = 2 + m} \\ \begin{gathered} f\left( 0 ight) = m \hfill \\ f\left( 1 ight) = - 4 + m \hfill \\ \end{gathered} \end{array}} ight. \Rightarrow \mathop {\min }\limits_{\left[ { - 1;1} ight]} f\left( x ight) = f\left( 1 ight) = - 4 + m \hfill \\ \Leftrightarrow \mathop {\min }\limits_{\left[ { - 1;1} ight]} f\left( x ight) = 0 \Rightarrow m = 4 \hfill \\ \end{matrix}

  • Câu 21: Vận dụng

    Cho hàm số y = f(x) có đạo hàm f'\left( x ight) = {x^2} - 2x,\forall x \in \mathbb{R}. Hàm số g\left( x ight) = f\left( {2 - \sqrt {{x^2} + 1} } ight) - \sqrt {{x^2} + 1} - 3 đồng biến trên các khoảng nào?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) có đạo hàm f'\left( x ight) = {x^2} - 2x,\forall x \in \mathbb{R}. Hàm số g\left( x ight) = f\left( {2 - \sqrt {{x^2} + 1} } ight) - \sqrt {{x^2} + 1} - 3 đồng biến trên các khoảng nào?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 22: Thông hiểu

    Một hãng điện thoại đưa ra quy luật bán buôn cho từng đại lí, đó là đại lí càng nhập nhiều chiếc điện thoại của hãng thì giá bán buôn một chiếc điện thoại càng giảm. Cụ thể, nếu đại lí mua x điện thoại thì giá tiền của mỗi điện thoại là 4000-2x(nghìn đồng), x \in N^{*},x < 2000. Đại lí nhập cùng một lúc bao nhiêu chiếc điện thoại thì hãng có thể thu về nhiều tiền nhất từ đại lí đó?

    Đáp án: 1000||1 000

    Đáp án là:

    Một hãng điện thoại đưa ra quy luật bán buôn cho từng đại lí, đó là đại lí càng nhập nhiều chiếc điện thoại của hãng thì giá bán buôn một chiếc điện thoại càng giảm. Cụ thể, nếu đại lí mua x điện thoại thì giá tiền của mỗi điện thoại là 4000-2x(nghìn đồng), x \in N^{*},x < 2000. Đại lí nhập cùng một lúc bao nhiêu chiếc điện thoại thì hãng có thể thu về nhiều tiền nhất từ đại lí đó?

    Đáp án: 1000||1 000

    Số tiền hãng thu được khi đại lí nhập x chiếc điện thoại là f(x) = x(4000 - 2x).

    Ta có: f'(x) = - \ 4x + 4000.

    Khi đó, f'(x) = 0 \Leftrightarrow x = 1\ 000 \Rightarrow f(x) = 2000000

    Học sinh tự vẽ bảng biến thiên

    Ta suy ra:

    Đại lí nhập cùng lúc 1\ 000 chiếc điện thoại thì hãng có thể thu nhiều tiền nhất từ đại lí đó với 2 000 000 000(đồng).

    Đáp số: 1000.

  • Câu 23: Nhận biết

    Số đường tiệm cận của đồ thị hàm số y = \frac{x}{x^{2} - 1} là:

    Tập xác định D\mathbb{= R}\backslash\left\{ \pm 1 ight\}

    Ta có: \lim_{x ightarrow \pm \infty}\frac{x}{x^{2} - 1} = \lim_{x ightarrow \pm \infty}\frac{\frac{1}{x}}{1 - \frac{1}{x^{2}}} = 0 suy ra tiệm cận ngang của đồ thị hàm số y = \frac{x}{x^{2} - 1} là y = 0.

    Lại có \lim_{x ightarrow 1^{+}}\frac{x}{x^{2} - 1} = + \infty;\lim_{x ightarrow 1^{-}}\frac{x}{x^{2} - 1} = - \infty suy ra x = 1 là tiệm cận đứng của đồ thị hàm số.

    \lim_{x ightarrow ( - 1)^{+}}\frac{x}{x^{2} - 1} = - \infty;\lim_{x ightarrow ( - 1)^{-}}\frac{x}{x^{2} - 1} = + \infty suy ra x = - 1 là tiệm cận đứng của đồ thị hàm số.

    Vậy có tất cả 3 đường tiệm cận.

  • Câu 24: Thông hiểu

    Tìm tất cả các giá trị thực của tham số m để hàm số y= \dfrac{2\cot x + 1}{\cot x + m} đồng biến trên khoảng \left( \frac{\pi}{4};\frac{\pi}{2} ight)?

    Điều kiện xác định \cot x eq - m

    Ta có: y' = \dfrac{-\dfrac{2}{\sin^{2}x}\left( \cot x + m ight) + \dfrac{1}{\sin^{2}}(2\cot x +1)}{\left( \cot x + m ight)^{2}}

    = \dfrac{1 - 2m}{\sin^{2}x.\left( \cot x +m ight)^{2}}

    Hàm số đồng biến trên khoảng \left( \frac{\pi}{4};\frac{\pi}{2} ight) khi và chỉ khi

    \left\{ \begin{matrix} y' > 0 \\ - m otin (0;1) \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 1 - 2m > 0 \\ \left\lbrack \begin{matrix} m \leq - 1 \\ m \geq 0 \\ \end{matrix} ight.\ \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} m \leq - 1 \\ m \geq 0 \\ \end{matrix} ight.\ \Leftrightarrow m \in ( - \infty; - 1brack \cup \left\lbrack 0;\frac{1}{2} ight)

    Vậy đáp án cần tìm là m \in ( - \infty; - 1brack \cup \left\lbrack 0;\frac{1}{2} ight).

  • Câu 25: Nhận biết

    Đường cong ở hình dưới đây là đồ thị của hàm số nào?

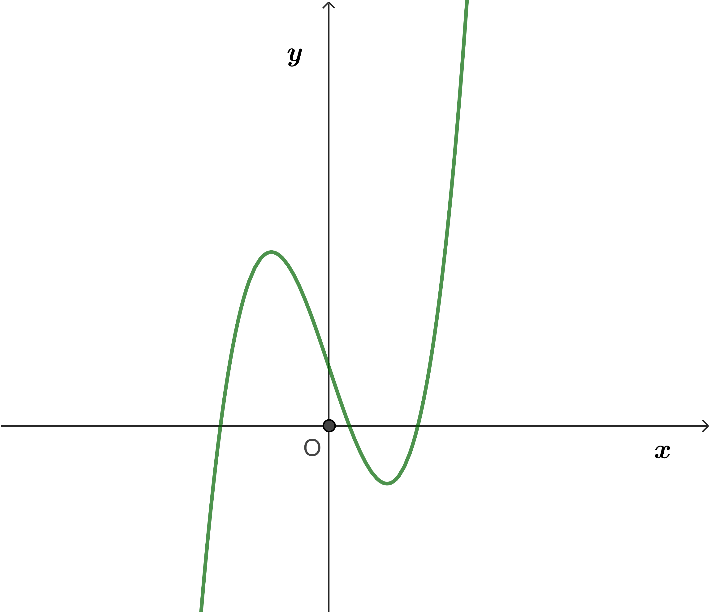
    Đồ thị của hàm số

    Dựa vào hình vẽ ta thấy đây là hàm số bậc ba có dạng y = a{x^3} + b{x^2} + cx + d;\left( {a > 0} ight)

  • Câu 26: Vận dụng cao

    Cho hàm số y = f(x) có đạo hàm f'\left( x ight) = x\left( {x - 1} ight)\left( {x - 2} ight),\forall x \in \mathbb{R}. Hàm số g\left( x ight) = f\left( {\frac{{5x}}{{{x^2} + 4}}} ight) đồng biến trên khoảng nào trong các khoảng sau?

    Ta có: f'\left( x ight) = 0 \Leftrightarrow x{\left( {x - 1} ight)^2}\left( {x - 2} ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 1} \\ {x = 2} \end{array}} ight.

    Ta có: g'\left( x ight) = \frac{{ - 5{x^2} + 20}}{{{{\left( {{x^2} + 4} ight)}^2}}}.f'\left( {\frac{{5x}}{{{x^2} + 4}}} ight)

    Cho g’(x) = 0 => \frac{{ - 5{x^2} + 20}}{{{{\left( {{x^2} + 4} ight)}^2}}}.f'\left( {\frac{{5x}}{{{x^2} + 4}}} ight) = 0

    Dựa vào f’(x) ta có:

    \left[ {\begin{array}{*{20}{c}} { - 5{x^2} + 20 = 0} \\ {\dfrac{{5x}}{{{x^2} + 4}} = 0} \\ {\dfrac{{5x}}{{{x^2} + 4}} = 1} \\ {\dfrac{{5x}}{{{x^2} + 4}} = 2} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \pm 2} \\ {x = 0} \\ {x = 1} \\ {x = 4} \end{array}} ight.

    Lập bảng xét dấu như sau:

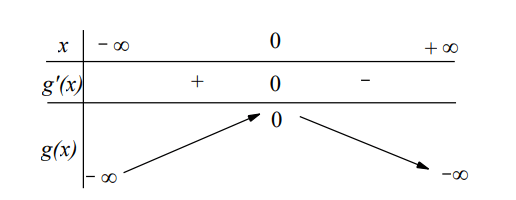
    Xét khoảng đồng biến của hàm số

    Quan sát bảng xét dấy ta suy ra hàm số đồng biến trên khoảng (2; 4)

  • Câu 27: Thông hiểu

    Cho hàm số y = 2x^{3} - 3x^{2} - m. Trên đoạn \lbrack - 1;1brack hàm số có giá trị nhỏ nhất là - 1. Tìm giá trị của m?

    Ta có: y' = 6x^{2} - 6x \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight.

    Ta có bảng biến thiên như sau:

    Từ bảng biến thiên suy ra \min_{\lbrack - 1;1brack}y = - 5 - m \Leftrightarrow - 1 = - 5 - m \Leftrightarrow m = - 4.

    Vậy m = - 4 là giá trị cần tìm.

  • Câu 28: Vận dụng

    Cho biết \left( P ight):y = {x^2} và điểm A\left( { - 2;\frac{1}{2}} ight). Gọi M là điểm bất kì thuộc (P). Khoảng cách MA nhỏ nhất là:

    Vì M thuộc (P)

    => \begin{matrix} M\left( {a;{a^2}} ight) \Rightarrow \overrightarrow {AM} = \left( {a + 2;{a^2} - \dfrac{1}{2}} ight) \hfill \\ \hfill \\ \end{matrix}

    \Rightarrow M{A^2} = {\left( {a + 2} ight)^2} + {\left( {{a^2} - \frac{1}{2}} ight)^2} = {a^4} - 4a + \frac{{17}}{4}

    Xét hàm số f\left( a ight) = {a^4} + 4a + \frac{{17}}{4} ta có:

    \begin{matrix} f'\left( a ight) = 4{a^3} + a \hfill \\ f'\left( a ight) = 0 \Rightarrow a = - 1 \hfill \\ \Rightarrow \min f\left( a ight) = f\left( { - 1} ight) = 1 - 4 + \dfrac{{17}}{4} = \dfrac{5}{4} \hfill \\ \Rightarrow M{A_{\min }} = \sqrt {\dfrac{5}{4}} = \dfrac{{\sqrt 5 }}{2} \hfill \\ \end{matrix}

  • Câu 29: Nhận biết

    Giá trị nhỏ nhất của hàm số y = \frac{x^{3} - 3x}{x + 1} trên đoạn \lbrack 0;2brack bằng:

    Ta có: y' = \frac{x^{2} + 2x - 3}{(x + 1)^{2}}

    \Rightarrow y' = 0 \Leftrightarrow \frac{x^{2} + 2x - 3}{(x + 1)^{2}} = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 3 \\ \end{matrix} ight.. Khi đó \left\{ \begin{matrix}y(0) = 0 \\y(2) = - \dfrac{2}{3} \\y(1) = - 1 \\\end{matrix} ight.\ \Rightarrow \min_{\lbrack 0;2brack}y = y(1) = -1.

  • Câu 30: Thông hiểu

    Đồ thị của hàm số nào trong bốn hàm số sau có đường tiệm ngang?

    Ta có:

    y = \frac{x}{1 + \sqrt{x}} không có tiệm cận ngang vì \lim_{x ightarrow + \infty}\frac{x}{1 + \sqrt{x}} = + \infty

    y = x^{3} - 3x không có tiệm cận ngang vì \lim_{x ightarrow \pm \infty}\left( x^{3} - 3x ight) = \pm \infty

    y = \log_{2}x không có tiệm cận ngang vì \lim_{x ightarrow + \infty}\left(\log_{2}x ight) = + \infty

    y = x + \sqrt{x^{2} + 4} có tiệm cận ngang vì \left\{ \begin{gathered} \mathop {\lim }\limits_{x \to + \infty } \left( {x + \sqrt {{x^2} + 4} } ight) = + \infty \hfill \\ \mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} + 4} } ight) = 0 \hfill \\ \end{gathered} ight.

  • Câu 31: Thông hiểu

    Cho hàm số y = \frac{mx - 18}{x -2m}. Giả sử S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng (2; + \infty). Xác định tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \frac{mx - 18}{x -2m}. Giả sử S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng (2; + \infty). Xác định tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 32: Nhận biết

    Cho hàm số y = f(x) xác định trên \mathbb{R}\backslash\left\{ - 1 ight\} liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

    Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

    Từ bảng biến thiên ta thấy:

    \lim_{x ightarrow - 1^{+}}y = - \infty suy ra x = - 1 là tiệm cận đứng.

    \lim_{x ightarrow - \infty}y = 2 suy ra y = 2 là tiệm cận ngang

    \lim_{x ightarrow - \infty}y = - 1 suy ra y = - 1 là tiệm cận ngang

    Vậy đồ thị hàm số đã cho có tất cả ba đường tiệm cận.

  • Câu 33: Thông hiểu

    Cho hàm số y = \frac{\sqrt{4 - x}}{\sqrt{x + 1}}. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

    Tập xác định D = ( - 1;4brack suy ra đồ thị hàm số không có đường tiệm cận ngang và đường tiệm cận xiên

    \lim_{x ightarrow ( - 1)^{+}}y = + \infty suy ra đồ thị nhận đường thẳng x = - 1 làm tiệm cận đứng.

    Vậy đồ thị hàm số có một đường tiệm cận.

  • Câu 34: Nhận biết

    Hàm số y = 2{x^3} - {x^2} + 5 có cực đại là:

    Ta có:

    \begin{matrix} y' = 6{x^2} - 2x \Rightarrow y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = \dfrac{1}{3}} \end{array}} ight. \hfill \\ y'' = 12x - 2 \Rightarrow y''\left( 0 ight) = - 2 < 0 \hfill \\ \end{matrix}

    => x = 0 là điểm cực đại của hàm số

  • Câu 35: Thông hiểu

    Hàm số y = f(x) có bảng biến thiên như sau:

    Phương trình f(x) = m có ba nghiệm thực phân biệt khi và chỉ khi:

    Số nghiệm của phương trình f(x) = m bằng số giao điểm của hai đồ thị hàm số \left\{ \begin{matrix} y = f(x) \\ y = m \\ \end{matrix} ight..

    Dựa vào bảng biến thiên ta có phương trình f(x) = m có ba nghiệm thực phân biệt khi và chỉ khi - 2 < m < 2.

  • Câu 36: Nhận biết

    Đồ thị hàm số nào có dạng đường trong như trong hình vẽ dưới đây?

    Dựa vào hình dáng đồ thị suy ra đồ thị hàm số bậc 4 trùng phương có hệ số a < 0 nên hàm số cần tìm là y = - 2x^{4} + 4x^{2} + 1.

  • Câu 37: Vận dụng cao

    Cho hàm số y = \frac{{x - 1}}{{\sqrt {4{x^2} - 2x - m} - x - 1}}. Xác định tất cả giá trị của tham số m để đồ thị hàm số có đúng 4 đường tiệm cận.

    Ta có: \mathop {\lim }\limits_{x \to + \infty } y = 1;\mathop {\lim }\limits_{x \to - \infty } y = - \frac{1}{3}=> Đồ thị hàm số có 2 đường tiệm cận ngang là y = 1 và y = - \frac{1}{3}

    Đồ thị có đúng 4 đường tiệm cận thì phương trình \sqrt {4{x^2} - 2x - m} - x - 1 = 0 có hai nghiệm phân biệt khác 1

    Ta có:

    \begin{matrix} \sqrt {4{x^2} - 2x - m} - x - 1 = 0 \hfill \\ \Leftrightarrow \sqrt {4{x^2} - 2x - m} = x + 1 \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant - 1} \\ {3{x^2} - 4x - 1 = m\left( * ight)} \end{array}} ight. \hfill \\ \end{matrix}

    Theo yêu cầu bài toán tương đương phương trình (*) có hai nghiệm phân biệt x \geqslant - 1,x e 1

    Xét hàm số y = 3{x^2} - 4x - 1;\left( {x \geqslant - 1;x e 1} ight)

    Bảng biến thiên

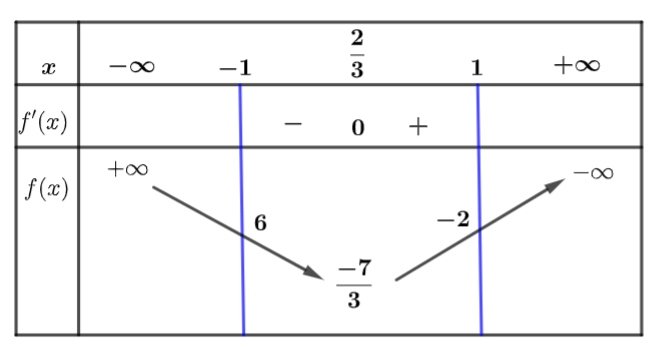
    Tìm m để đồ thị hàm số có đúng 4 đường tiệm cận

    Dựa vào bảng biến thiên phương trình 3{x^2} - 4x - 1 = m;\left( {x \geqslant - 1;x e 1} ight) có hai nghiệm thì m \in \left( {\frac{{ - 7}}{3};6} ight]\backslash \left\{ { - 2} ight\}

  • Câu 38: Thông hiểu

    Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x^{3} - 3x^{2} + (4 - m)x đồng biến trên khoảng (2; + \infty) là:

    Tập xác định D\mathbb{= R}

    Ta có: y' = 3x^{2} - 6x + 4 - m

    Hàm số đồng biến trên khoảng (2; + \infty) \Leftrightarrow y' \geq 0;\forall x \in (2; + \infty)

    \Leftrightarrow m \leq 3x^{2} - 6x + 4;\forall x \in (2; + \infty)

    Xét hàm số g(x) = 3x^{2} - 6x + 4 trên khoảng (2; + \infty).

    Ta có: g'(x) = 6x - 6;g'(x) = 0 \Leftrightarrow x = 1

    Ta có bảng biến thiên

    Dựa vào bảng biến thiên ta có: m \leq g(x);;\forall x \in (2; + \infty) \Leftrightarrow m \leq 4

    Vậy m \leq 4 thỏa mãn yêu cầu bài toán.

  • Câu 39: Nhận biết

    Cho hàm số y = f(x) liên tục trên \lbrack 2;5brack và có đồ thị như hình vẽ:

    Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \lbrack 2;5brack lần lượt là M;m. Kết luận nào sau đây đúng?

    Quan sát đồ thị ta thấy \left\{\begin{matrix}\max_{\lbrack 2;5brack}y = M = 4 \\\min_{\lbrack 2;5brack}y = m = - 6 \\\end{matrix} ight.\ \Rightarrow M - m = 10

  • Câu 40: Thông hiểu

    Đồ thị hàm số nào dưới đây có đúng một đường tiệm cận ngang?

    Xét hàm số y = \frac{4x - 2}{x^{2} - 3x + 2} có tập xác định D\mathbb{= R}\backslash\left\{ 1;2 ight\}

    Ta có: \left\{ \begin{gathered} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{4x - 2}}{{{x^2} - 3x + 2}}} ight) = 0 \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{4x - 2}}{{{x^2} - 3x + 2}}} ight) = 0 \hfill \\ \end{gathered} ight.suy ra y = 0 là một tiệm cận ngang của đồ thị hàm số.

    Vậy hàm số có duy nhất một tiệm cận ngang là y = \frac{4x - 2}{x^{2} - 3x + 2}.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 10 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập