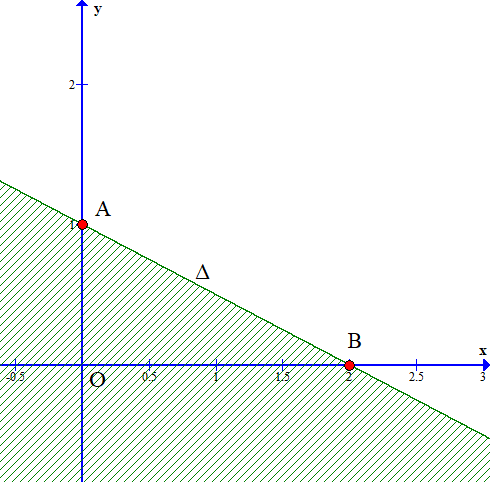
Ta thấy đường thẳng ∆ cắt 2 trục tọa độ tại điểm A(0; 1) và B(2; 0).
Xét đáp án 
Thay x = 0, y = 1 vào phương trình x + 2y – 2 = 0 ta được 0 + 2. 1 – 2 = 0 = 0 là mệnh đề đúng.
Thay x = 2, y = 0 vào phương trình x + 2y – 2 = 0 ta được 2 + 2.0 – 2 = 0 = 0 là mệnh đề đúng.
Thay x = 0, y = 0 vào bất phương trình x + 2y – 2 > 0 ta được 0 + 2.0 – 2 = -2 > 0 là mệnh đề sai, vậy điểm O(0; 0) không thỏa mãn bất phương trình, nên miền nghiệm của bất phương trình x + 2y – 2 > 0 là bờ đường thẳng x + 2y – 2 = 0, không chứa điểm O.
Vậy  đúng.
đúng.
Xét đáp án 
Thay x = 0, y = 1 vào phương trình 3x + y – 2 = 0 ta có 3. 0 + 1 – 2 = -1 = 0 là mệnh đề sai, vậy câu  sai.
sai.
Xét đáp án 
Thay x = 0, y = 1 vào phương trình x - 2y + 1 = 0 ta có 0 - 2. 1 + 1 = -1 = 0 là mệnh đề sai, vậy câu  sai.
sai.
Xét đáp án 
Thay x = 0, y = 1 vào phương trình x + 3y = 0 ta có 0 + 3. 1 = 3 = 0 là mệnh đề sai, vậy câu  sai.
sai.
![]() có tập nghiệm
có tập nghiệm ![]() . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng? là nghiệm của phương trình (2) nhưng không phải là nghiệm của phương trình (1). Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng
.








 .
.