Lớp 12 Toán 12

Đề kiểm tra 45 phút Chương 2 Mặt nón, mặt trụ, mặt cầu

Mô tả thêm: Nội dung các câu hỏi trong Đề kiểm tra được thay đổi liên tục giúp học sinh ôn tập kiến thức và kĩ năng một cách tốt hơn
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

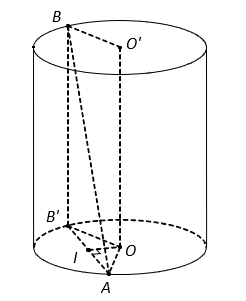
    Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R\sqrt 3. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 30^0. Khoảng cách giữa AB và trục của hình trụ bằng:

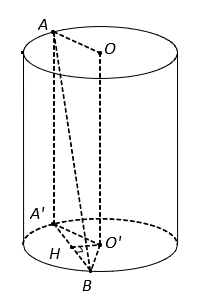
    Tính khoảng cách

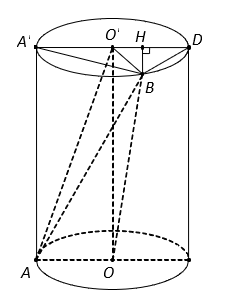
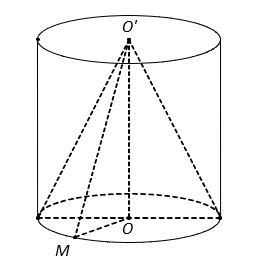
    Từ hình vẽ kết hợp với giả thiết, ta có OA = O'B = R.

    Gọi AA’ là đường sinh của hình trụ thì O'A' = R,{m{ }}AA' = R\sqrt 3 và \widehat {BAA'} = {30^0}.

    Vì OO'\parallel \left( {ABA'} ight) nên d\left[ {OO',\left( {AB} ight)} ight] = d\left[ {OO',\left( {ABA'} ight)} ight] = d\left[ {O',\left( {ABA'} ight)} ight].

    Gọi H là trung điểm A’B, suy ra \left. \begin{array}{l}O'H \bot A'B\\O'H \bot AA'\end{array} ight\} \Rightarrow O'H \bot \left( {ABA'} ight)

    nên O'H = \frac{{R\sqrt 3 }}{2}h.

    Tam giác ABA’ vuông tại A’ nên BA' = AA'\tan {30^0} = R

    Suy ra tam giác A’BO đều có cạnh bằng R nên O'H = \frac{{R\sqrt 3 }}{2}.h

  • Câu 2: Vận dụng cao

    Trong không gian Oxyz, cho điểm A(1;2;-1) và mặt phẳng (P):x+y+2z-13=0. Xét các mặt cầu (S) có tâm I(a;b;c), đi qua điểm A, tiếp xúc với mặt phẳng (P) . Tính giá trị của biểu thức T=a^2+2b^2+3c^2 khi (S) có bán kính nhỏ nhất.

     Gọi H là hình chiếu của I trên mặt phẳng (P) ta có IA + IH =2R nên R nhỏ nhất khi I, A, H thẳng hàng và I là trung điểm của AH.

    Phương trình AH đi qua A và vuông góc với mặt phẳng (P) có phương trình là

    \left\{\begin{matrix} x=1+t \\ y=2+t \\ z=-1+2t \end{matrix}ight.

    Tọa độ H là nghiệm (x;y;z) của hệ:

    \left\{\begin{matrix} x=1+t \\ y=2+t \\ z=-1+2t \\ x+y+2z-13=0 \end{matrix}ight.

    \Rightarrow H(3;4;3)\Rightarrow I(2;3;1)

    Suy ra, ta có: T=a^2+2b^2+3c^2 =2^2+2.3^2+3.1^2=25

  • Câu 3: Thông hiểu

    Bán kính đáy hình trụ bằng 4 cm, chiều cao bằng 6cm. Độ dài đường chéo của thiết diện qua trục bằng:

     Thiết diện qua trục của một hình trụ là một hình chữ nhật có hai cạnh lần lượt bằng đường kính đáy và chiều cao của hình trụ.

    Vậy hai cạnh của hình chữ nhật là 8 cm và 6 cm.

    Do đó độ đài đường chéo: \sqrt {{8^2} + {6^2}} = 10{m{cm}}{m{.}}

  • Câu 4: Thông hiểu

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:

     Gọi bán kính đáy là R.

    Từ giả thiết suy ra h= 2a và chu vi đáy bằng a .

    Do đó 2\pi R = a \Leftrightarrow R = \frac{a}{{2\pi }}.

  • Câu 5: Vận dụng cao

    Trong không gian với hệ tọa độ Oxyz, cho điểm A(0; 8; 2), điểm B(9; −7; 23) và mặt cầu (S) : (x − 5)^2 + (y + 3)^2 + (z − 7)^2 = 72. Gọi (P) là mặt phẳng qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Biết \vec{n} = (1; m; n) là một vectơ pháp tuyến của (P). Tính mn.

    Mặt cầu (S) có tâm I(5; −3; 7); bán kính R = 6\sqrt{2}.

    Phương trình mặt phẳng (P) : 1(x − 0) + m(y − 8) + n(z − 2) = 0.

    Vì (P) và (S) tiếp xúc nhau nên:

    d\left( I;(P) ight) = R \Leftrightarrow \frac{|5 - 11m + 5n|}{\sqrt{1 + m^{2} + n^{2}}} = 6\sqrt{2}

    \Leftrightarrow |5 - 11m + 5n| = 6\sqrt{2}\sqrt{1 + m^{2} + n^{2}}(*)

    Ta có: d\left( B;(P) ight) = \frac{|9 - 15m + 21n|}{\sqrt{1 + m^{2} + n^{2}}}

    Ta có:

    |9 - 15m + 21n| = |5 - 11m + 5n + 4 - 4m + 16n|

    \leq |5 - 11m + 5n| + |4 - 4m + 16n|(**)

    Áp dụng BĐT Bunhiacopxki ta có

    (4 - 4m + 16n)^{2} \leq \left( 4^{2} + 4^{2} + 16^{2} ight)\left( 1 + m^{2} + n^{2} ight) = 288\left( 1 + m^{2} + n^{2} ight)

    \Rightarrow |4 - 4m + 16n| \leq 12\sqrt{2}.\sqrt{1 + m^{2} + n^{2}}(***)

    Từ (*); (**); (***) ta có:

    |9 - 15m + 21n| \leq 18\sqrt{2}\sqrt{1 + m^{2} + n^{2}}

    Dấu “=” xảy ra khi và chỉ khi: \left\{\begin{matrix}|5 - 11m + 5n| = 6\sqrt{2}\sqrt{1 + m^{2} + n^{2}} \\(5 - 11m + 5n)(4 - 4m + 16n) \geq 0 \\\dfrac{1}{4} = \dfrac{m}{- 4} = \dfrac{n}{16} \\\end{matrix} ight.

    \Rightarrow m = - 1;n = 4 \Rightarrow mn = - 4.

  • Câu 6: Vận dụng

    Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA và SB, biết tam giác SAB vuông và có diện tích bằng 4a^2. Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng 30^0. Đường cao h của hình nón bằng:

     Tính đường cao nón

    Theo giả thiết ta có tam giác SAB vuông cân tại S.

    Gọi E là trung điểm AB, suy ra\left\{ \begin{array}{l}SE \bot AB\\OE \bot AB\end{array} ight.  và SE = \frac{1}{2}AB.

    Ta có {S_{\Delta SAB}} = \frac{1}{2}AB.SE = 4{a^2} \Leftrightarrow \frac{1}{2}AB.\frac{1}{2}AB = 4{a^2}

    \Rightarrow AB = 4a \Rightarrow SE = 2a.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH.

    Từ đó suy ra OH \bot \left( {SAB} ight) nên

    {30^0} = \widehat {SO,\left( {SAB} ight)} = \widehat {SO,SH} = \widehat {OSH} = \widehat {OSE}

    Trong tam giác vuông SOE, ta có SO = SE.\cos \widehat {OSE} = a\sqrt 3

  • Câu 7: Thông hiểu

    Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Nội tiếp hình nón là một hình chóp đỉnh S, đáy là hình vuông ABCD cạnh a. Nửa góc ở đỉnh của hình nón có tan bằng:

     Tính tang của góc

    Nửa góc ở đỉnh của hình nón là góc \widehat {ASO} .

    Hình vuông ABCD cạnh a nên suy ra: OA = \frac{{a\sqrt 2 }}{2}

    Trong tam giác vuông SOA, ta có \tan \widehat {ASO} = \frac{{OA}}{{SO}} = \frac{{a\sqrt 2 }}{{2h}}.

  • Câu 8: Thông hiểu

    Trong không gian Oxyz, cho các điểm A(1;0;0),C(0;0;3),B(0;2;0). Tập hợp các điểm M thỏa mãn MA^{2} = MB^{2} + MC^{2} là mặt cầu có bán kính là:

    Giả sử M(x;y;z)

    Ta có:\left\{ \begin{matrix} MA^{2} = (x - 1)^{2} + y^{2} + z^{2} \\ MB^{2} = x^{2} + (y - 2)^{2} + z^{2} \\ MC^{2} = x^{2} + y^{2} + (z - 3)^{2} \\ \end{matrix} ight.

    Theo bài ra ta có:

    MA^{2} = MB^{2} + MC^{2}

    \Leftrightarrow (x - 1)^{2} + y^{2} + z^{2} = x^{2} + (y - 2)^{2} + z^{2} + x^{2} + y^{2} + (z - 3)^{2}

    \Leftrightarrow - 2x + 1 = (y - 2)^{2} + x^{2} + (z - 3)^{2}

    \Leftrightarrow (x + 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 2

    Vậy tập hợp điểm M thỏa mãn MA^{2} = MB^{2} + MC^{2} là mặt cầu có bán kính là R = \sqrt{2}.

  • Câu 9: Vận dụng

    Cho hình trụ có hai đáy là hai hình tròn (O) và(O’), thiết diện qua trục của hình trụ là hình vuông. Gọi A, B là hai điểm lần lượt nằm trên hai đường tròn (O) và(O’). Biết AB = 2a và khoảng cách giữa hai đường thẳng AB và OO’ bằng \frac{{a\sqrt 3 }}{2}. Bán kính đáy bằng:

     Tính bán kính

    Dựng đường sinh BB', gọi I là trung điểm của AB’, ta có

    \left\{ \begin{array}{l}OI \bot AB'\\OI \bot BB'\end{array} ight. \Rightarrow OI \bot \left( {ABB'} ight)

    Suy ra d\left[ {AB,OO'} ight] = d\left[ {OO',\left( {ABB'} ight)} ight] = d\left[ {O,\left( {ABB'} ight)} ight] = OI = \frac{{a\sqrt 3 }}{2}.

    Gọi bán kính đáy của hình trụ là R.

    Vì thiết diện qua trục của hình trụ là hình vuông nên OO' = BB' = 2R

    Trong tam giác vuông A B’B, ta có AB{'^2} = A{B^2} - B{B^2} = 4{a^2} - 4{R^2}.

    Trong tam giác vuông OIB’, ta có N OB{'^2} = O{I^2} + IB{'^2} \Leftrightarrow {R^2} = {\left( {\frac{{a\sqrt 3 }}{2}} ight)^2} + {\left( {\frac{{AB'}}{2}} ight)^2}.

    Suy ra AB{'^2} = 4{R^2} - 3{a^2}.

    Từ đó ta có 4{a^2} - 4{R^2} = 4{R^2} - 3{a^2} \Rightarrow R = \frac{{a\sqrt {14} }}{4}.

  • Câu 10: Nhận biết

    Trong không gian Oxyz, cho các mặt cầu dưới đây. Hỏi mặt cầu nào có bán kính R = 2?

    Phương trình mặt cầu (S):x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0 có bán kính R = \sqrt{a^{2} + b^{2} + c^{2} - d}

    Xét phương trình mặt cầu (S):x^{2} + y^{2} + z^{2} - 4x + 2y + 2z + 2 = 0 ta có:

    \left\{ \begin{matrix} a = 2;b = - 1 \\ c = - 1;d = 2 \\ \end{matrix} ight.\ \Rightarrow R = \sqrt{a^{2} + b^{2} + c^{2} - d} = \sqrt{4} = 2

  • Câu 11: Thông hiểu

    Gọi (S) là mặt cầu đi qua bốn điểm A(2;0;0),B(1;3;0),C( - 1;0;3),D(1;2;3). Tính bán kính R của (S)?

    Gọi I(a;b;c) là tâm mặt cầu đi qua bốn điểm A;B;C;D

    Khi đó ta có phương trình:

    \left\{ \begin{matrix} AI^{2} = BI^{2} \\ AI^{2} = CI^{2} \\ AI^{2} = DI^{2} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} (a - 2)^{2} + b^{2} + c^{2} = (a - 1)^{2} + (b - 3)^{2} + c^{2} \\ (a - 2)^{2} + b^{2} + c^{2} = (a + 1)^{2} + b^{2} + (c - 3)^{2} \\ (a - 2)^{2} + b^{2} + c^{2} = (a - 1)^{2} + (b - 2)^{2} + (c - 3)^{2} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} a - 3b = - 3 \\ a - c = - 1 \\ a - 2b - 3c = - 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} a = 0 \\ b = 1 \\ c = 1 \\ \end{matrix} ight.\ \Rightarrow I(0;1;1)

    Vậy bán kính cần tìm là: R = IA = \sqrt{2^{2} + 1^{2} + 1^{2}} = \sqrt{6}

  • Câu 12: Thông hiểu

    Với giá trị nào của m thì mặt phẳng \left( Q ight):x + y + z + 3 = 0 cắt mặt cầu

    \left( S ight):{x^2} + {y^2} + {z^2} - 2\left( {m + 1} ight)x + 2my - 2mz + 2{m^2} + 9 = 0?

    Theo đề bài, ta xác định các hệ số của (S):

    a = m + 1;b = - m;c = m;d = 2{m^2} + 9.

    Suy ra tâm I có tọa độ là I\left( {m + 1, - m,m} ight)

    \Rightarrow {R^2} = {\left( {m + 1} ight)^2} + {m^2} + {m^2} - 2{m^2} - 9 = {m^2} + 2m - 8 > 0

    \Rightarrow m < - 4 \vee m > 2

    (P) cắt (S) khi:

    d\left( {I,P} ight) < R \Leftrightarrow \frac{{\left| {m + 4} ight|}}{{\sqrt 3 }} < \sqrt {{m^2} + 2m - 8} \Leftrightarrow m < - 4 \vee m > 5

  • Câu 13: Thông hiểu

    Trong không gian Oxyz, cho mặt phẳng (P):2x + 2y + z - 2 = 0 và mặt cầu (S) tâm I(2;1; - 1) bán kính R = 2. Bán kính đường tròn giao của mặt phẳng (P) và mặt cầu (S) là:

    Hình vẽ minh họa

    Gọi bán kính đường tròn giao của mặt phẳng (P) và mặt cầu (S) là r

    Ta có:

    h = d\left( I;(P) ight) = \frac{\left| 2.2 + 2.( - 1) - 1 - 2 ight|}{\sqrt{2^{2} + 2^{2} + 1^{2}}} = 1

    Suy ra r = \sqrt{2^{2} - 1^{2}} = \sqrt{3}

  • Câu 14: Nhận biết

    Xét các mệnh đề:

    (I) Tập hợp các đường thẳng d thay đổi nhưng luôn luôn song song và cách đường thẳng \triangle cố định một khoảng không đổi là một mặt trụ.

    (II) Hai điểm A, B cố định. Tập hợp các điểm M trong không gian mà diện tích tam giác MAB không đổi là một mặt trụ.

    Trong các mệnh đề trên, mệnh đề nào đúng?

    Ta xét về khái niệm Mặt trụ suy ra  (I) đúng.

    Diện tích tam giác MAB không đổi khi và chỉ khi khoảng cách từ M đến đường thẳng AB không đổi (giả sử bằng R ).

    Vậy tập hợp các điểm M là mặt trụ bán kính R và trục là AB.

    Vì vậy Mệnh đề (II) cũng đúng.

  • Câu 15: Nhận biết

    Trong không gian, cho tam giác ABC vuông tại A, AB =a và AC = a\sqrt 3. Độ dài đường sinh \ell của hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng:

    Độ dài đường sinh

    Từ giả thiết suy ra hình nón có đỉnh là B , tâm đường tròn đáy là A , bán kính đáy là AC = a\sqrt 3 và chiều cao hình nón là AB = a.

    Vậy độ dài đường sinh của hình nón là:

    \ell = BC = \sqrt {A{B^2} + A{C^2}} = 2a.

  • Câu 16: Vận dụng

    Cho mặt cầu (S): {x^2} + {y^2} + {z^2} - 4x + 6y + 2z - 2 = 0 và điểm A\left( { - 6, - 1,3} ight). Gọi M là tiếp điểm của (S) và tiếp tuyến di động qua (d). Tìm tập hợp các điểm M.

    (Có thể chọn nhiều đáp án)

     Theo đề bài, (S) có tâm I\left( {2, - 3,1} ight).\,\overrightarrow {IM} = \left( {x - 2,y + 3,z + 1} ight);\,\,\overrightarrow {AM} = \left( {x + 6,y + 1,z - 3} ight)

    Ta có:

    \begin{array}{l}\overrightarrow {IM} .\overrightarrow {AM} = \left( {x - 2} ight)\left( {x + 6} ight) + \left( {y + 3} ight)\left( {y + 1} ight) + \left( {z + 1} ight)\left( {z - 3} ight) = 0\\ \Rightarrow M \in \left( {S'} ight):{x^2} + {y^2} + {z^2} + 4x + 4y - 3z - 12 = 0;\,\,M \in \left( S ight)\end{array}

    \Rightarrow M \in  đường tròn  \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} - 4x + 6y + 2z - 2 = 0\\4x - y - 2z - 5 = 0\end{array} ight.

    Hay \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} + 4x + 4y - 2z - 12 = 0\\4x - y - 2z - 5 = 0\end{array} ight.

  • Câu 17: Nhận biết

    Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh S là ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho SH = \frac{{3a}}{2}. Độ dài đường sinh \ell của hình nón bằng:

    Độ dài đường sinh

    Gọi S' là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.

    Tam giác SAS’ vuông tại A và có đường cao AH nên S{A^2} = SH.SS' \Rightarrow SA = a\sqrt 3 .

  • Câu 18: Thông hiểu

    Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng 60^0, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng \frac{R}{2}. Đường cao h của hình nón bằng:

    Theo giả thiết ta có tam giác OAB đều cạnh R.

    Gọi E là trung điểm AB, suy ra OE \bot AB và OE = \frac{{R\sqrt 3 }}{2}.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH

    Từ đó suy ra OH \bot \left( {SAB} ight) nên d\left[ {O,\left( {SAB} ight)} ight] = OH = \frac{R}{2}.

    Trong tam giác vuông SOE, ta có  \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{8}{{3{R^2}}} \Rightarrow SO = \frac{{R\sqrt 6 }}{4}

  • Câu 19: Nhận biết

    Cho đường tròn (C) đường kính AB và đường thẳng \triangle. Để hình tròn xoay sinh bởi (C) khi quay quanh \triangle là một mặt cầu thì cần có thêm điều kiện nào sau đây:

    Điều kiện để hình tròn xoay sinh bởi (C) khi quay quanh \triangle là một mặt cầu là trục quay \triangle phải cố định và hai điểm A, B cũng cố định trên \triangle.

  • Câu 20: Vận dụng cao

    Một hộp sữa hình trụ có thể tích V (không đổi) được làm từ một tấm tôn có diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa bán kính đáy R và đường cao h bằng:

    Công thức tính thể tích V = \pi {R^2}h , suy ra h = \frac{V}{{\pi {R^2}}}

    Hộp sữa chỉ kín một đáy nên diện tích tôn cần dùng là:

    {S_{tp}} = {S_{xq}} + {S_{{m{day}}}} = 2\pi Rh + \pi {R^2} = \frac{{2V}}{R} + \pi {R^2}

    Xét hàm f\left( R ight) = \frac{{2V}}{R} + \pi {R^2}  trên \left( {0; + \infty } ight) , ta được \mathop {\min }\limits_{\left( {0; + \infty } ight)} f\left( R ight) đạt tại R=h.

  • Câu 21: Thông hiểu

    Cho hình trụ có chiều cao bằng 8a . Biết hai điểm A và C lần lượt nằm trên hai đáy thỏa mãn AC=10a, khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:

      Thể tích của khối trụ

    Gọi (O) và (O') lần lượt là hai đường tròn đáy; A\in (O), C \in (O') .

    Dựng AD, CB lần lượt song song với OO' (D \in (O'), B \in (O). Dễ dàng có ABCD là hình chữ nhật.

    Do AC=10a,AD=8a\Rightarrow DC=6a..

    Gọi H là trung điểm của DC.

    \left\{\begin{matrix}O^\prime H\bot D C\\O^\prime H\bot A D\\\end{matrix}\Rightarrow O^\prime H\bot(ABCD)ight..

    Ta có O^\prime//(ABCD)\Rightarrow d\left(OO^\prime,ACight)=d\left(OO^\prime,(ABCD)ight)=O^\prime H=4a..

    Suy ra O^\prime H=4a,CH=3a\Rightarrow R=O^\prime C=5a..

    Vậy thể tích của khối trụ là V=\pi R^2h=\pi(5a)^28a=200\pi a^3.

  • Câu 22: Thông hiểu

    Trong không gian với hệ toạ độ Oxyz, cho phương trìnhx^{2} + y^{2} + z^{2} - 2x - 4y - 6z - 11 = 0. Viết phương trình mặt phẳng (\alpha), biết (\alpha) song song với mặt phẳng (P):2x + y - 2z + 11 = 0 và cắt mặt cầu theo thiết diện là một đường tròn có chu vi 8\pi?

    Vì (α) // (P) nên phương trình mặt phẳng (α) có dạng 2x + y - 2z + c = 0

    Mặt cầu (S) có tâm I(1; 2; 3) và bán kính R = 5.

    Đường tròn lớn có chu vi là 8\pi nên bán kính của (S) là \frac{8\pi}{2\pi} = 4

    Khoảng cách từ tâm I đến mặt phẳng P bằng 3

    Từ đó ta có:

    d\left( I;(P) ight) = \frac{|2.1 + 2 - 2.3 + c|}{\sqrt{2^{2} + 1^{2} + ( - 2)^{2}}} = 3

    \Leftrightarrow | - 2 + c| = 9 \Leftrightarrow \left\lbrack \begin{matrix} c = 11 \\ c = - 7 \\ \end{matrix} ight.

    Vì (α) // (P) nên phương trình mặt phẳng (α) là 2x + y - 2z - 7 = 0

  • Câu 23: Vận dụng

    Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính bằng chiều cao và bằng a. Trên đường tròn tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B sao cho AB = 2a. Thể tích của khối tứ diện OO’AB bằng:

     Tính thể tích khối trụ

    Kẻ đường sinh AA’, gọi D là điểm đối xứng với A’ qua tâm O’ và H là hình chiếu của B trên A’D.

    Ta có BH \bot \left( {AOO'A'} ight) nên {V_{OO'AB}} = \frac{1}{3}{S_{\Delta AOO'}}.BH.

    Trong tam giác vuông A'AB có A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt 3 a.

    Trong tam giác vuông A'BD có BD = \sqrt {A'{D^2} - A'{B^2}} = a.

    Do đó suy ra tam giác BO'D nên BH = \frac{{\sqrt 3 a}}{2}.

    Vậy  {V_{OO'AB}} = \frac{1}{3}.\left( {\frac{1}{2}{a^2}} ight).\frac{{a\sqrt 3 }}{2} = \frac{{\sqrt 3 {a^3}}}{{12}} (đvtt).

  • Câu 24: Vận dụng cao

    Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S): (x-1)^2+(y+1)^2+(z-2)^2=16 và điểm A(1;2;3) . Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.

    Tính tổng diện tích

    Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là (P), (Q), (R).

    Với điểm I bất kỳ, hạ II_1, II_2, II_3 lần lượt vuông góc với ba mặt phẳng (P), (Q), (R) thì ta luôn có: IA^2 = II_1 ^2+ II_2^2, II_3 ^2(1) .

    Thật vậy , ta chọn hệ trục tọa độ Oxyz với O\equiv A , ba trục Ox, Oy, Oz lần lượt là ba giao tuyến của ba mặt phẳng (P), (Q), (R)..

    Khi đó tọa độ I(a;b;c) thì:

    IA^2=a^2+b^2+c^2=d^2(A;(Iyz))+d^2(A;(Ixz))+d^2(A;(Ixy))

    hay IA^2=II_1^2+II_2^2+II_3^2.

    Vậy (1) được chứng minh.

    Tính tổng diện tích

    Áp dụng giải bài:

    Mặt cầu (S) có tâm I(1;-1;2) và có bán kính r=4.

    \overrightarrow {IA}=(0;3;1) \Rightarrow IA= \sqrt {10}.

    Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là (P), (Q), (R) và cắt mặt cầu (S) theo ba đường tròn lần lượt là(C_1),(C_2),(C_3).

    Gọi I_1, I_2, I_3 và  r_1, r_2, r_3 lần lượt là tâm và bán kính của (C_1),(C_2),(C_3).

    Khi đó : II_1\perp (P) \Rightarrow II_1^2+r_1^2=r^2 \Rightarrow r_1^2=r^2-II_1^2.

    Tương tự có: r_2^2=r^2-II_2^2  và  r_3^2=r^2-II_3^2.

    Theo nhận xét ở trên ta có: IA^2=II_1^2+II_2^2+II_3^2

    Ta có tổng diện tích các đường tròn là :

    S= \pi(r_1^2+r_2^2+r_3^2)=\pi(r^2-II_1^2+r^2-II_2^2+r^2-II_3^2)

    =\pi[3r^2-(II_1^2+II_2^2+II_3^2)]

    =\pi(3r^2-IA^2)=38 \pi.

  • Câu 25: Vận dụng cao

    Cho hình nón có bán kính đáy là 5a , độ dài đường sinh là 13a. Thể tích khối cầu nội tiếp hình nón bằng:

    Thể tích khối cầu nội tiếp hình nón

    Xét mặt phẳng qua trục SO của hình nón ta được thiết diện là tam giác cân SAB.

    Mặt phẳng đó cắt mặt cầu theo đường tròn có bán kính r (bán kính mặt cầu) và nội tiếp trong tam giác cân SAB.

    Trong tam giác vuông SOB, gọi I là giao điểm của đường phân giác trong góc B với đường thẳng SO.

    Chứng minh được I là tâm đường tròn nội tiếp tam giác và bán kínhr =IO=IE  (E là hình chiếu vuông góc của I trên SB).

    Theo tính chất phân giác, ta có \frac{{IS}}{{IO}} = \frac{{BS}}{{BO}} = \frac{{13}}{5}.

    Lại có IS + IO = SO = \sqrt {S{B^2} - O{B^2}} = 12.

    Từ đó suy ra IS = \frac{{26}}{3},{m{ }}IO = \frac{{10}}{3}.

    Ta có \Delta SEI \backsim\Delta SOB  nên \frac{{IE}}{{IS}} = \frac{{BO}}{{BS}} = \frac{5}{{13}} \Rightarrow IE = \frac{5}{{13}}IS = \frac{{10}}{3}

    Thể tích khối cầu: V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {\left( {\frac{{10a}}{3}} ight)^3} = \frac{{4000\pi {a^3}}}{{81}} (đvtt).

  • Câu 26: Nhận biết

    Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120^0. Diện tích toàn phần của hình nón là:

    Diện tích toàn phần

    Gọi S là đỉnh, O là tâm của đáy, thiết diện qua trục là SAB.

    Theo giả thiết, ta có SA = 2a và \widehat {ASO} = 60^\circ.

    Trong tam giác SAO vuông tại O, ta có

    OA = SA.\sin 60^\circ = a\sqrt 3

    Vậy diện tích toàn phần:

    {S_{tp}} = \pi R\ell + \pi {R^2} = \pi .OA.SA + \pi {\left( {OA} ight)^2} = \pi {a^2}\left( {3 + 2\sqrt 3 } ight) (đvdt).

  • Câu 27: Nhận biết

    Hình nón có đường sinh l=2a và hợp với đáy góc \alpha = {60^0}. Diện tích toàn phần của hình nón bằng:

    Diện tích toàn phần

    Theo giả thiết, ta có

    SA = \ell = 2a và \widehat {SAO} = {60^0}.

    Suy ra:

    R = OA = SA.\cos {60^0} = a.

    Vậy diện tích toàn phần của hình nón bằng: S = \pi Rl + \pi {R^2} = 3\pi {a^2} (đvdt). 

  • Câu 28: Vận dụng

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3; 1; 2) và B(5; 7; 0). Có tất cả bao nhiêu giá trị thực của tham số m để phương trình x^{2} + y^{2} + z^{2} - 4x + 2my - 2(m + 1)z + m^{2} + 2m + 8 = 0 là phương trình của một mặt cầu (S) sao cho qua hai điểm A, B có duy nhất một mặt phẳng cắt mặt cầu (S) đó theo giao tuyến là một đường tròn có bán kính bằng 1.

    Ta có:

    x^{2} + y^{2} + z^{2} - 4x + 2my - 2(m + 1)z + m^{2} + 2m + 8 = 0

    \Leftrightarrow (x - 2)^{2} + (y + m)^{2} + (z - m - 1)^{2} = m^{2} - 3(*)

    Suy ra (*) là phương trình mặt cầu

    \Leftrightarrow m^{2} - 3 > 0 \Leftrightarrow |m| > \sqrt{3}

    Khi đó, mặt cầu (S) có tâm I(2; −m; m + 1) và bán kính R = \sqrt{m^{2} - 3}

    Gọi (P) là mặt phẳng đi qua A, B.

    Theo giả thiết (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính r = 1.

    Mặt khác, khoảng cách từ tâm I đến mặt phẳng (P) là d = \sqrt{R^{2} - r^{2}} = \sqrt{m^{2} - 4};\left( m^{2} - 4 \geq 0 ight)

    Ta có: \overrightarrow{AB} = (2;6; - 2) suy ra \overrightarrow{u} = (1;3; - 1) là một vectơ chỉ phương của đường thẳng AB

    Suy ra đường thẳng AB là: \left\{ \begin{matrix} x = 3 + t \\ y = 1 + 3t \\ z = 2 - t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)

    Để có duy nhất mặt phẳng (P) thỏa mãn bài thì

    TH1. Mặt phẳng (P) đi qua điểm I và I otin AB

    Ta có I ∈ (P) ⇔ d = 0 ⇔ m^2 − 4 = 0 ⇔ m = ±2.

    + Với m = 2 ⇒ I(2; −2; 3) ∈ AB ⇒ m = 2 (loại).

    + Với m = −2 ⇒ I(2;2; - 1) otin AB⇒ m = −2 (thỏa mãn).

    TH2. Mặt phẳng (P) cách I một khoảng lớn nhất ⇔ d lớn nhất ⇔ d = d(I, AB). (*)

    \overrightarrow{IA} = (1;1 + m;1 - m)

    \Rightarrow \left\lbrack \overrightarrow{IA};\overrightarrow{u} ightbrack = ( - 4 + 2m;2 - m;2 - m)

    \Rightarrow \left| \left\lbrack \overrightarrow{IA};\overrightarrow{u} ightbrack ight| = |2 - m|\sqrt{6};\left| \overrightarrow{u} ight| = \sqrt{11}

    Khi đó d(I;AB) = \frac{\left| \left\lbrack \overrightarrow{IA};\overrightarrow{u} ightbrack ight|}{\left| \overrightarrow{u} ight|} = \frac{|2 - m|\sqrt{6}}{\sqrt{11}}

    (*) \Leftrightarrow \sqrt{m^{2} - 4} = \frac{|2 - m|\sqrt{6}}{\sqrt{11}}

    \Leftrightarrow 5m^{2} + 24m - 68 = 0\Leftrightarrow \left\lbrack \begin{matrix}m = 2(ktm) \\m = - \dfrac{34}{5}(tm) \\\end{matrix} ight.

    Vậy có 2 giá trị tham số m thỏa mãn yêu cầu.

  • Câu 29: Nhận biết

    Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt cầu có tâm I(7;6; - 5) và bán kính 9?

    Mặt cầu tâm I(7;6; - 5), bán kính R = 9 có phương trình lá:

    (x - 7)^{2} + (y - 6)^{2} + (z - 5)^{2} = 81.

  • Câu 30: Thông hiểu

    Cho hình trụ có hai đáy là hai hình tròn (O) và (O’), chiều cao R\sqrt 3 và bán kính đáy R. Một hình nón có đỉnh là O’ và đáy là hình tròn (O;R). Tỉ số diện tích xung quanh của hình trụ và hình nón bằng:

    Tỉ số diện tích

    Diện tích xung quanh của hình trụ:

    {S_{{m{xq}}\left( {m{T}} ight)}} = 2\pi R.h = 2\pi R.R\sqrt 3 = 2\sqrt 3 \pi {R^2} (đvdt).

    Kẻ đường sinh O’M của hình nón, suy ra

    \ell = O'M = \sqrt {OO{'^2} + O{M^2}} = \sqrt {3{R^2} + {R^2}} = 2R.

    Diện tích xung quanh của hình nón: {S_{{m{xq}}\left( {m{N}} ight)}} = \pi R\ell = \pi R.2R = 2\pi {R^2} (đvdt).

    Vậy \frac{{{S_{{m{xq}}\left( {m{T}} ight)}}}}{{{S_{{m{xq}}\left( {m{N}} ight)}}}} = \sqrt 3.

  • Câu 31: Thông hiểu

    Trong hệ tọa độ Oxyz, cho mặt cầu (S) có đường kính AB, với A(6;2; - 5),B( - 4;0;7). Viết phương trình (P) tiếp xúc với mặt cầu (S) tại A?

    Hình vẽ minh họa

    Vì mặt cầu (S) có đường kính là AB nên tâm I của mặt cầu (S) là trung điểm của AB.

    Mặt cầu (S) có tâm I(1; 1; 1).

    Vì (P) tiếp xúc với (S) tại A nên (P) đi qua A và nhận \overrightarrow{IA} = (5;1; - 6) làm vectơ pháp tuyến.

    Suy ra (P):5(x - 6) + (y - 2) - 6(z + 5) = 0

    \Rightarrow (P):5x + y - 6z - 62 = 0

  • Câu 32: Thông hiểu

    Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng:

    Diện tích toàn phần

    Theo giả thiết ta được hình trụ có chiều cao h=AB=1 , bán kính đáy R = \frac{{AD}}{2} = 1

    Do đó diện tích toàn phần: {S_{tp}} = 2\pi Rh + 2\pi {R^2} = 4\pi

  • Câu 33: Vận dụng

    Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là \frac{a}{2}. Thể tích của khối nón ngoại tiếp hình chóp SABC bằng:

     Thể tích khối nón

    Gọi E là trung điểm của BC, dựng OH \bot SE tại H.

    Chứng minh được OH \bot \left( {SBC} ight) nên suy ra OH = d\left[ {O,\left( {SBC} ight)} ight] = \frac{a}{2}.

    Trong tam giác đều ABC, ta có OE = \frac{1}{3}AE = \frac{1}{3}.\frac{{2a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}

    và  OA = \frac{2}{3}AE = \frac{{2a\sqrt 3 }}{3}

    Trong tam giác vuông SOE, ta có

    \frac{1}{{O{H^2}}} = \frac{1}{{O{E^2}}} + \frac{1}{{S{O^2}}} \Rightarrow \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{1}{{{a^2}}} \Rightarrow SO = a.

    Vậy thể tích khối nón V = \frac{1}{3}\pi O{A^2}.SO = \frac{1}{3}\pi {\left( {\frac{{2a\sqrt 3 }}{3}} ight)^2}.a = \frac{{4\pi {a^3}}}{9}  (đvtt).

  • Câu 34: Vận dụng

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3; −2; 6), B(0; 1; 0) và mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 25. Mặt phẳng (P): ax + by + cz + d = 0 (với a, b, c là các số nguyên dương và a, b, c, d nguyên tố cùng nhau) đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính tổng T = a + b + c.

    Hình vẽ minh họa

    Ta có \overrightarrow{AB} = ( - 3;3; - 6) cùng phương với \overrightarrow{u} = (1; - 1;2) suy ra phương trình đường thẳng AB:\left\{ \begin{matrix} x = t \\ y = 1 - t \\ z = 2t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight).

    Xét mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 25⇒ I(1; 2; 3), R = 5.

    Gọi H(t; 1 − t; 2t) là điểm trên AB sao cho AB ⊥ IH

    \Rightarrow \overrightarrow{IH} = (t - 1; - t - 1;2t)

    Vì AB ⊥ IH ⇒ t − 1 + t + 1 + 4t − 6 = 0 ⇒ t = 1⇒ H(1; 0; 2), \overrightarrow{IH} = (0; - 2; - 1)

    Gọi r là bán kính đường tròn giao tuyến giữa (P) và (S), K là hình chiếu vuông góc của I lên (P) ⇒ IK ≤ IH.

    Ta có r = \sqrt{R^{2} - IK^{2}} \geq \sqrt{R^{2} - IH^{2}}

    Dấu bằng chỉ xảy ra khi K ≡ H.

    Khi đó phương trình mặt phẳng (P) nhận \overrightarrow{IH} = (0; - 2; - 1) là vectơ pháp tuyến và đi qua điểm H(1; 0; 2) là 2y + z − 2 = 0 ⇒ T = 3

  • Câu 35: Nhận biết

    Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S):x^{2} + y^{2} + z^{2} - 2y + 2z - 7 = 0. Bán kính của mặt cầu (S) là:

    Ta có:

    x^{2} + y^{2} + z^{2} - 2y + 2z - 7 = 0

    \Leftrightarrow x^{2} + y^{2} + z^{2} - 2.0.x - 2.1y - 2.( - 1)z - 7 = 0

    \Leftrightarrow \left\{ \begin{matrix} a = 0 \\ b = 1 \\ c = - 1 \\ d = - 7 \\ \end{matrix} ight. suy ra tâm mặt cầu là: I(0;1; - 1)

    Bán kính mặt cầu là:

    R = \sqrt{a^{2} + b^{2} + c^{2} - d} = \sqrt{0^{2} + 1^{2} + ( - 1)^{2} - 7} = 3

  • Câu 36: Nhận biết

    Trong không gian với hệ toạ độ Oxyz, mặt cầu (S):(x - 1)^{2} + y^{2} + (z + 3)^{2} = 16 có tâm là

    Mặt cầu (S):(x - 1)^{2} + y^{2} + (z + 3)^{2} = 16 có tâm là: I(1;0; - 3) .

  • Câu 37: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm nằm trên mặt phẳng (Oxy) và đi qua ba điểm A(1;2; - 4),B(1; - 3;1),C(2;2;3). Tọa độ tâm I của mặt cầu (S) là:

    Gọi tâm mặt cầu là I(a;b;c) và phương trình mặt cầu (S):x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0

    Do I \in (Oxy) \Rightarrow c = 0

    \Rightarrow (S):x^{2} + y^{2} + z^{2} - 2ax - 2by + d = 0

    Lại có \left\{ \begin{matrix} A \in (S) \\ B \in (S) \\ C \in (S) \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 2a + 4b - d = 21 \\ 2a - 6b - d = 11 \\ 4a + 4b - d = 17 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} a = - 2 \\ b = 1 \\ d = - 21 \\ \end{matrix} ight.

    Vậy I( - 2;1;0) là đáp án cần tìm.

  • Câu 38: Vận dụng

    Trong không gian Oxyz, cho A(5; 0; 0), B(1; 2; −4), C(4; 3; 0) và mặt phẳng (α): x + 2y + 2z − 10 = 0. Viết phương trình mặt cầu đi qua A, B, C và tiếp xúc mặt phẳng (α).

    Gọi I(x; y; z) là tâm mặt cầu cần tìm.

    Theo bài ra ta có:

    \left\{ \begin{matrix} AI = IB \\ AI = CI \\ AI = d\left( I;(\alpha) ight) \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}\sqrt{(x - 5)^{2} + y^{2} + z^{2}} = \sqrt{(x - 1)^{2} + (y - 2)^{2} +(z + 4)^{2}} \\\sqrt{(x - 5)^{2} + y^{2} + z^{2}} = \sqrt{(x - 4)^{2} + (y - 3)^{2} +z^{2}} \\\sqrt{(x - 5)^{2} + y^{2} + z^{2}} = \dfrac{|x + 2y + 2z -10|}{\sqrt{1^{2} + 2^{2} + 2^{2}}} \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} 2x - y + 2z = 1 \\ x - 3y = 0 \\ 3\sqrt{(x - 5)^{2} + y^{2} + z^{2}} = |x + 2y + 2z - 10| \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}x = 3y \\z = \dfrac{- 5y + 1}{2} \\65y^{2} - 130y + 65 = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x = 3 \\y = 1 \\z = - 2 \\\end{matrix} ight.

    Vậy phương trình mặt cầu tâm I(3; 1; −2) bán kính R = AI = 3 là (x - 3)^{2} + (y - 1)^{2} + (z + 2)^{2} = 9.

  • Câu 39: Thông hiểu

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:

     Gọi bán kính đáy là R.

    Hình trụ có chu vi đáy bằng 2a nên ta có 2\pi R = 2a \Leftrightarrow R = \frac{a}{\pi }.

    Suy ra hình trụ này có đường cao h=a.

    Vậy thể tích khối trụ V = \pi {R^2}h = \pi {\left( {\frac{a}{\pi }} ight)^2}a = \frac{{{a^3}}}{\pi }(đvtt).

  • Câu 40: Thông hiểu

    Một hình trụ có bán kính đáy R = 70{m{cm}} , chiều cao hình trụ h = 20{m{cm}}. Một hình vuông có các đỉnh nằm trên hai đường tròn đáy sao cho có ít nhất một cạnh không song song và không vuông góc với trục hình trụ. Khi đó cạnh của hình vuông bằng bao nhiêu?

    Tính độ dài cạnh

    Xét hình vuông ABCD có AD không song song và không vuông góc với trục OO’ của hình trụ.

    Dựng đường sinh AA', ta có \left\{ \begin{array}{l}CD \bot AA'\\CD \bot AD\end{array} ight. \Rightarrow CD \bot \left( {AA'D} ight) \Rightarrow CD \bot A'D.

    Suy ra A’C là đường kính đáy nên A'C = 2R = 140{m{cm}}{m{.}}

    Xét tam giác vuông AA’C, ta có AC = \sqrt {AA{'^2} + A'{C^2}} = 100\sqrt 2 {m{cm}}{m{.}}

    Suy ra cạnh hình vuông bằng 100 cm.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 2 Mặt nón, mặt trụ, mặt cầu Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 2 Mặt nón, mặt trụ, mặt cầu
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập