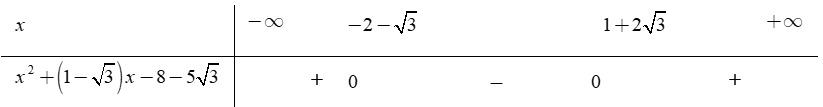Tổng các nghiệm của phương trình ![]() là
là
ĐKXĐ: x ≥ 0
Dễ thấy x = 0 không phải là nghiệm của phương trình
Xét x > 0, phương trình
Đặt
Phương trình trở thành
• Với t = 1 ta có (thỏa mãn)
• Với t = 2 ta có (thỏa mãn)
Vậy phương trình có nghiệm là và x = 1.
Tổng các nghiệm của phương trình là .








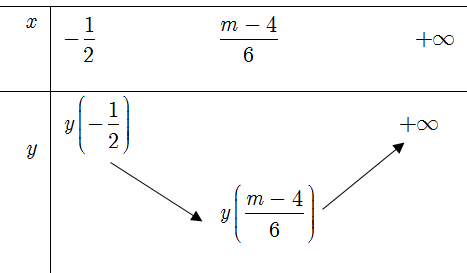
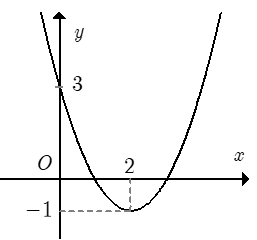
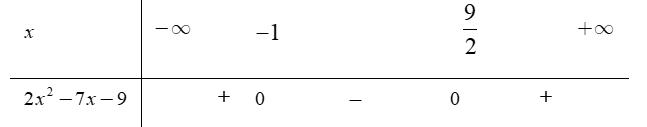
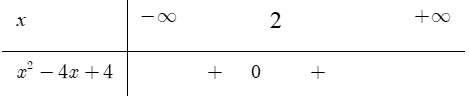
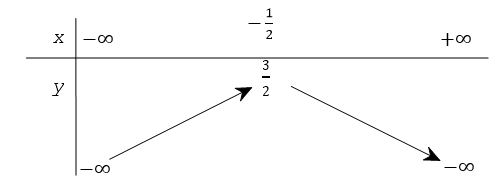
 là?
là?