Lớp 10 Toán 10 - Kết nối tri thức

Đề kiểm tra 45 phút Chương 3 Hệ thức lượng trong tam giác KNTT

Mô tả thêm: Đề kiểm tra 1 tiết Toán 10 Hệ thức lượng trong tam giác gồm 40 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Kết nối tri thức.
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho tam giác ABC thỏa mãn BC^{2} + AC^{2} - AB^{2} - \sqrt{2}BC.AC = 0. Khi đó, góc C có số đo là:

    Theo đề bài ra ta có:

    BC^{2} + AC^{2} - AB^{2} - \sqrt{2}BC.AC = 0

    \Leftrightarrow BC^{2} + AC^{2} - AB^{2} = \sqrt{2}BC.AC

    \Leftrightarrow \frac{BC^{2} + AC^{2} - AB^{2}}{BC \cdot AC} = \sqrt{2}

    \Leftrightarrow 2\cos C - \sqrt{2} = 0

    \Leftrightarrow \cos C = \frac{\sqrt{2}}{2}\Rightarrow \widehat{C} = 45^{\circ}.

  • Câu 2: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sin\alpha,\ tan\alpha trái dấu?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai thì \sin\alpha > 0, \cos\alpha < 0.

    Điểm cuối của \alpha thuộc góc phần tư thứ tư thì \sin\alpha < 0, \cos\alpha > 0.

    Vậy nếu \sin\alpha,\ cos\alpha trái dấu thì điểm cuối của góc lượng giác \alpha ở góc phần tư thứ II hoặc IV.

  • Câu 3: Thông hiểu

    Cho \frac{\pi}{2} < \alpha < \pi. Giá trị lượng giác nào sau đây luôn dương?

    Ta có \sin(\pi + \alpha) = - \sin\alpha; \cot\left( \frac{\pi}{2} - \alpha ight) = \sin\alpha; \cos( - \alpha) = \cos\alpha; \tan(\pi + \alpha) = \tan\alpha.

    Do \frac{\pi}{2} < \alpha < \pi ightarrow \left\{ \begin{matrix} \sin\alpha > 0 \\ \cos\alpha < 0 \\ \tan\alpha < 0 \\ \end{matrix} ight..

  • Câu 4: Nhận biết

    Trong các khẳng định sau, khẳng định nào là đúng?

     Ta có: \sin157^{\circ} =\sin (180^{\circ} -157^{\circ} )=\sin 23^{\circ}. Vì \sin \alpha =\sin (180^{\circ} -\alpha ).

  • Câu 5: Nhận biết

    Cho \Delta ABC vuông tại B và có \widehat{C} = 25^{0}. Số đo của góc A là:

    Ta có: Trong \Delta ABC \widehat{A} + \widehat{B} + \widehat{C} = 180^{0} \Rightarrow \widehat{A} = 180^{0} - \widehat{B} - \widehat{C} = 180^{0} - 90^{0} - 25^{0} = 65^{0}.

  • Câu 6: Nhận biết

    Cho tam giác ABC có a = 8,b = 10, góc C bằng 60^{0} . Độ dài cạnh c là ?

    Ta có: c^{2} = a^{2} + b^{2} - 2a.b.cosC = 8^{2} + 10^{2} - 2.8.10.cos60^{0} = 84 \Rightarrow c = 2\sqrt{21}.

  • Câu 7: Nhận biết

    Cho tam giác ABC có AB =4cm;AC = 12cm và góc \widehat{BAC} = 120^{\circ}. Tính diện tích tam giác ABC.

    S = \frac{1}{2}AB \cdot AC \cdot \sin\widehat{BAC}

    = \frac{1}{2} \cdot 4 \cdot 12 \cdot \sin 120^{\circ}

    = 12\sqrt{3}\left( {cm}^{2}ight)

  • Câu 8: Thông hiểu

    Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:

    Áp dụng hệ quả định lí cosin cho tam giác ABC ta có:

    \begin{matrix} \cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \hfill \\ \Rightarrow \cos \widehat A = \dfrac{{{{15}^2} + {{13}^2} - {{24}^2}}}{{2.15.13}} = - \dfrac{7}{{15}} \hfill \\ \Rightarrow \widehat A \approx {117^0}49\prime \hfill \\ \end{matrix}

  • Câu 9: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sqrt{sin^{2}}\alpha = \sin\alpha.

    Ta có \sqrt{sin^{2}\alpha} \Leftrightarrow \sin\alpha \Leftrightarrow \left| \sin\alpha ight| = \sin\alpha.

    Đẳng thức \left| \sin\alpha ight| = \sin\alpha\overset{}{ightarrow}\sin\alpha \geq 0\overset{}{ightarrow}điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc II.

  • Câu 10: Vận dụng

    Cho góc \alpha thỏa mãn \cot\alpha = \frac{1}{3}. Tính P = \frac{3sin\alpha + 4cos\alpha}{2sin\alpha - 5cos\alpha}.

    Chia cả tử và mẫu của P cho \sin\alpha ta được P = \frac{3 + 4cot\alpha}{2 - 5cot\alpha} = \frac{3 + 4.\frac{1}{3}}{2 - 5.\frac{1}{3}} = 13.

  • Câu 11: Nhận biết

    Chọn công thức đúng trong các đáp án sau:

    Ta có: S = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B = \frac{1}{2}ab\sin C.

  • Câu 12: Thông hiểu

    Giá trị biểu thức A = \sin {30^0}.\cos {60^0} + \sin {60^0}.\cos {30^0} là:

    Ta có:

    \begin{matrix} A = \sin {30^0}.\cos {60^0} + \sin {60^0}.\cos {30^0} \hfill \\ A = \dfrac{1}{2}.\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} \hfill \\ A = \dfrac{1}{4} + \dfrac{3}{4} = 1 \hfill \\ \end{matrix}

  • Câu 13: Thông hiểu

    Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?

    Hình ảnh minh họa

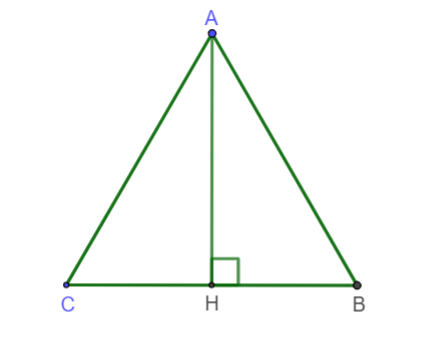
    Chọn khẳng định đúng

    Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường phân giác

    => \widehat {BAH} = \frac{1}{2}\widehat {BAC}=30^0;\widehat {ABC} = {60^0};\widehat {AHC} = {90^0}

    Do đó: \sin \widehat {BAH} = \frac{1}{2};\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}

    Ta có: \widehat {ABC} = {60^0} \Rightarrow \sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}

  • Câu 14: Nhận biết

    Cho tam giác ABC có AB = 12,AC = 13,BC = 5. Diện tích S của tam giác ABC là:

    Ta có: BA^{2} + BC^{2} = AC^{2} nên tam giác ABC vuông tại B.

    Diện tích tam giác là: S = \frac{1}{2}BA \cdot BC = 30.

  • Câu 15: Vận dụng

    Tính giá trị của \cos\left\lbrack \frac{\pi}{4} + (2k + 1)\pi ightbrack.

    Ta có \cos\left\lbrack \frac{\pi}{4} + (2k + 1)\pi ightbrack = \cos\left( \frac{5\pi}{4} + 2k\pi ight) = \cos\frac{5\pi}{4}

    = \cos\left( \pi + \frac{\pi}{4} ight) = - \cos\frac{\pi}{4} = - \frac{\sqrt{2}}{2}.

  • Câu 16: Nhận biết

    Giá trị cot\frac{\pi }{6} là:

     Ta có: cot\frac{\pi }{6} =\sqrt3.

  • Câu 17: Nhận biết

    Cho tam giác ABC có AB=1;AC=\sqrt2;\hat A=45^{\circ}. Tính độ dài cạnh BC.

     Áp dụng định lí côsin:

    BC^2=AB^2+AC^2-2.AB.AC.\cos A=1+2-2.1.\sqrt2.\cos45^{\circ} =1.

    Suy ra BC=1.

  • Câu 18: Thông hiểu

    Cho tam giác ABC, chọn công thức đúng trong các đáp án sau:

    Ta có: m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4} = \frac{2b^{2} + 2c^{2} - a^{2}}{4}.

  • Câu 19: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha > 0 \\ \tan\alpha < 0 \\ \cot\alpha < 0 \\ \end{matrix} ight..

  • Câu 20: Thông hiểu

    Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230m. Góc giữa hai hàng rào MN và MP là 110^{\circ} (như hình vẽ)

    Diện tích mảnh đất mà gia đình bà Sáu sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?

    Diện tích mảnh đất của gia đình bà Sáu (tam giác MNP) là:

    S = \frac{1}{2}MN \cdot MP \cdot \sin M

    = \frac{1}{2} \cdot 150 \cdot 230 \cdot \sin110^{\circ} \approx 16209,7\left( {m}^{2}ight).

  • Câu 21: Thông hiểu

    Cho góc \alpha thỏa mãn \cos\alpha = - \frac{\sqrt{5}}{3} và \pi < \alpha < \frac{3\pi}{2}. Tính \tan\alpha.

    Ta có \left\{ \begin{matrix} \sin\alpha = \pm \sqrt{1 - cos^{2}\alpha} = \pm \frac{2}{3} \\ \pi < \alpha < \frac{3\pi}{2} \\ \end{matrix} ight. \overset{}{ightarrow}\sin\alpha = - \frac{2}{3}\overset{}{ightarrow}\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{2}{\sqrt{5}}.

  • Câu 22: Nhận biết

    Tam giác ABC có \hat B = {60^0},\hat C = {45^0};AC = 5. Độ dài cạnh AB là:

    Áp dụng định lí sin trong tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin B}} = \dfrac{{AB}}{{\sin C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin C}}{{\sin B}} = \dfrac{{5.\sin {{45}^0}}}{{\sin {{60}^0}}} = \dfrac{{5\sqrt 6 }}{3} \hfill \\ \end{matrix}

  • Câu 23: Nhận biết

    Tam giác ABC có BC = 10 và \widehat{A}=30°. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

     Ta có: \frac {BC}{\sin A}=2R \Leftrightarrow R= \frac{BC}{2\sin A} =\frac {10}{2.sin30^{\circ} }=10.

  • Câu 24: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha < 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 25: Vận dụng cao

    Cho tam giác ABC thỏa mãn biểu thức

    \dfrac{4 - 2\sin^{2}\widehat{B} -2\sin^{2}\widehat{C}}{\sin^{2}\widehat{B} + \sin^{2}\widehat{C}} = \left(\cot\widehat{B} + \cot\widehat{C} ight)^{2} -2\cot\widehat{B}.\cot\widehat{C}

    Chọn khẳng định đúng.

    Ta có:

    \dfrac{4 - 2\sin^{2}\widehat{B} -2\sin^{2}\widehat{C}}{\sin^{2}\widehat{B} + \sin^{2}\widehat{C}} = \left(\cot\widehat{B} + \cot\widehat{C} ight)^{2} -2\cot\widehat{B}.\cot\widehat{C}

    \Leftrightarrow\dfrac{4}{\sin^{2}\widehat{B} + \sin^{2}\widehat{C}} - 2 =\cot^{2}\widehat{B} + \cot^{2}\widehat{C}

    \Leftrightarrow\dfrac{4}{\sin^{2}\widehat{B} + \sin^{2}\widehat{C}} - 2 =\dfrac{1}{\sin^{2}\widehat{B}} + \dfrac{1}{\sin^{2}\widehat{C}} -2

    \Leftrightarrow \left(\sin^{2}\widehat{B} + \sin^{2}\widehat{C} ight)\left(\dfrac{1}{\sin^{2}\widehat{B}} + \dfrac{1}{\sin^{2}\widehat{C}} ight) =4

    \Leftrightarrow\dfrac{\sin^{2}\widehat{B}}{\sin^{2}\widehat{C}} +\dfrac{\sin^{2}\widehat{C}}{\sin^{2}\widehat{B}} - 2 = 0

    \Leftrightarrow \left(\dfrac{\sin\widehat{B}}{\sin\widehat{C}} -\dfrac{\sin\widehat{C}}{\sin\widehat{B}} ight)^{2} = 0

    \Leftrightarrow \sin\widehat{B} = \sin\widehat{C}

    \Leftrightarrow \widehat{B} = \widehat{C}

    Vậy tam giác ABC là tam giác cân.

  • Câu 26: Thông hiểu

    Trong tam giác ABC có AB = 2, AC = 1 và \widehat{A}=60^0. Tính độ dài cạnh BC.

    Áp dụng định lí cosin cho tam giác ABC ta có:

    \begin{matrix} B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A \hfill \\ \Leftrightarrow B{C^2} = {2^2} + {1^2} - 2.2.1.\cos {60^0} \hfill \\ \Leftrightarrow B{C^2} = 3 \hfill \\ \Leftrightarrow BC = \sqrt 3 \hfill \\ \end{matrix}

  • Câu 27: Nhận biết

    Tam giác ABC có \widehat{B} = 60{^\circ},\ \ \widehat{C} = 45{^\circ} và AB = 5. Tính độ dài cạnh AC.

    Theo định lí hàm sin, ta có \frac{AB}{\sin\widehat{C}} = \frac{AC}{\sin\widehat{B}} \Leftrightarrow \frac{5}{sin45{^\circ}} = \frac{AC}{sin60{^\circ}} \Rightarrow AC = \frac{5\sqrt{6}}{2}.

  • Câu 28: Thông hiểu

    Nếu tam giác ABC có BC^{2} < AB^{2} + AC^{2} thì:

    Nếu tam giác ABC có BC^{2} < AB^{2} + AC^{2} thì \widehat{A} là góc nhọn

  • Câu 29: Nhận biết

    Cho biết \tan\alpha = \frac{1}{2}. Tính \cot\alpha.

    Ta có: \tan\alpha.cot\alpha = 1 \Rightarrow \cot\alpha = \frac{1}{\tan\alpha} = \frac{1}{\frac{1}{2}} = 2.

  • Câu 30: Thông hiểu

    Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và \widehat{ACB} = 60{^\circ}. Tính độ dài cạnh cạnh BC.

    Gọi M,\ \ N lần lượt là trung điểm của AB,\ \ BC.

    \overset{}{ightarrow}MN là đường trung bình của \Delta ABC.

    \overset{}{ightarrow}MN = \frac{1}{2}AC. Mà MN = 3, suy ra AC = 6.

    Theo định lí hàm cosin, ta có:

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{ACB}

    \Leftrightarrow 9^{2} = 6^{2} + BC^{2} - 2.6.BC.cos60{^\circ}

    \Rightarrow BC = 3 + 3\sqrt{6}

  • Câu 31: Nhận biết

    Tam giác ABC có AB=5,BC=7,CA=8. Số đo góc \hat A bằng:

     Áp dụng định lí côsin:

    \cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}= \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}.

    Suy ra \hat A = 60^{\circ}.

  • Câu 32: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \cos\alpha = \sqrt{1 - sin^{2}\alpha}.

    Ta có \cos\alpha = \sqrt{1 - sin^{2}\alpha} \Leftrightarrow \cos\alpha = \sqrt{cos^{2}\alpha} \Leftrightarrow \cos\alpha = \left| \cos\alpha ight| \Leftrightarrow \cos\alpha.

    Đẳng thức \left| \cos\alpha ight| \Leftrightarrow \cos\alpha\overset{}{ightarrow}\cos\alpha \geq 0\overset{}{ightarrow}điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc IV.

  • Câu 33: Nhận biết

    Cho \Delta ABCcó a = 6,b = 8,c = 10. Diện tích S của tam giác trên là:

    Ta có: Nửa chu vi \Delta ABC: p = \frac{a + b + c}{2}.

    Áp dụng công thức Hê-rông: S = \sqrt{p(p - a)(p - b)(p - c)} = \sqrt{12(12 - 6)(12 - 8)(12 - 10)} = 24.

  • Câu 34: Vận dụng

    Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ vào gương màu xanh như hình vẽ. Biết OP = 2 m, OQ=\sqrt{2}+\sqrt{6}m

    Tính độ dài PT

    Khi đó đoạn PT bằng:

    Ta có: \left\{ {\begin{array}{*{20}{c}} {\widehat {SQB} = \widehat {PQT} = \alpha } \\ {\widehat {TOP} = \beta } \end{array}} ight.

    Áp dụng định lí cosin cho tam giác POQ ta có:

    \begin{matrix} P{Q^2} = O{P^2} + O{Q^2} - 2OP.OQ.\cos \widehat {POQ} \hfill \\ \Rightarrow P{Q^2} = {\left( {\sqrt 2 } ight)^2} + {\left( {\sqrt 2 + \sqrt 6 } ight)^2} - 2.\sqrt 2 .\left( {\sqrt 2 + \sqrt 6 } ight).\cos {45^0} \hfill \\ \Rightarrow PQ = 2\sqrt 2 \left( {cm} ight) \hfill \\ \end{matrix}

    Áp dụng hệ quả của định lí cosin cho tam giác POQ ta có:

    \begin{matrix} \cos \alpha = \cos \widehat {OQP} \hfill \\ \Rightarrow \cos \alpha = \dfrac{{O{Q^2} + P{Q^2} - O{P^2}}}{{2.OQ.PQ}} \hfill \\ \Rightarrow \cos \alpha = \dfrac{{{{\left( {\sqrt 2 + \sqrt 6 } ight)}^2} + {{\left( {2\sqrt 2 } ight)}^2} - {{\left( {\sqrt 2 } ight)}^2}}}{{2.\left( {\sqrt 2 + \sqrt 6 } ight).\sqrt 2 }} \hfill \\ \Rightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{2} \Rightarrow \alpha = {30^0} \hfill \\ \end{matrix}

    Ta lại có: \beta = {45^0} + \alpha = {45^0} + {30^0} = {75^0}

    => {\widehat {TPO}}=75^0

    Xét tam giác OTP ta có: 

    \begin{matrix} \widehat {OTP} + \widehat {TOP} + \widehat {TPO} = {180^0} \hfill \\ \Rightarrow \widehat {OTP} = {180^0} - \left( {\widehat {TOP} + \widehat {TPO}} ight) \hfill \\ \Rightarrow \widehat {OTP} = {180^0} - \left( {{{45}^0} + {{75}^0}} ight) \hfill \\ \Rightarrow \widehat {OTP} = {60^0} \hfill \\ \end{matrix}

    Áp dụng định lí sin cho tam giác OTP ta có:

    \begin{matrix} \dfrac{{OP}}{{\sin \widehat {OTP}}} = \dfrac{{PT}}{{\sin \widehat {TOP}}} \hfill \\ \Rightarrow PT = \dfrac{{OP.\sin \widehat {TOP}}}{{\sin \widehat {OTP}}} \hfill \\ \Rightarrow PT = \dfrac{{2.\sin {{45}^0}}}{{\sin {{60}^0}}} = \dfrac{{2\sqrt 6 }}{3} \hfill \\ \end{matrix}

  • Câu 35: Vận dụng

    Từ một đỉnh tháp chiều cao CD = 80\ m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 72^{0}12' và 34^{0}26' so với phương nằm ngang. Ba điểm A,B,D thẳng hàng. Tính khoảng cách AB (chính xác đến hàng đơn vị)?

    Ta có: Trong tam giác vuông CDA: tan72^{0}12' = \frac{CD}{AD} \Rightarrow AD = \frac{CD}{tan72^{0}12'} = \frac{80}{tan72^{0}12'} \simeq 25,7.

    Trong tam giác vuông CDB: tan34^{0}26' = \frac{CD}{BD} \Rightarrow BD = \frac{CD}{tan34^{0}26'} = \frac{80}{tan34^{0}26'} \simeq 116,7.

    Suy ra: khoảng cách AB = 116,7 - 25,7 = 91\ m.

  • Câu 36: Vận dụng cao

    Cho tam giác ABC có các góc thỏa mãn biểu thức

    \sin^{2}\widehat{A} + \sin^{2}\widehat{B}= \sqrt[2017]{\sin\widehat{C}}

    Giả sử AB = c;BC = a;AC = b. Tính số đo góc \widehat{C}?

    Ta có:

    \sin\widehat{C} \in \lbrack - 1;1brack \Rightarrow sin^{2017}\widehat{C} \geq sin^{2}\widehat{C}

    \Rightarrow sin^{2}\widehat{A} + sin^{2}\widehat{B} \geq sin^{2}\widehat{C}

    \Rightarrow 4R^{2}.\left\lbrack sin^{2}\widehat{A} + sin^{2}\widehat{B} ightbrack \geq 4R^{2}.sin^{2}\widehat{C}

    \Rightarrow a^{2} + b^{2} \geq c^{2}

    \Rightarrow a^{2} + b^{2} - c^{2} \geq 0

    Theo định lí cosin ta có:

    \Rightarrow \cos\widehat{C} = \frac{a^{2} + b^{2} - c^{2}}{2ab} \geq 0

    Ta thấy

    \sin^{2}\widehat{A} + \sin^{2}\widehat{B}= \frac{1 - \cos2\widehat{A}}{2} + \frac{1 -\cos2\widehat{B}}{2}

    = 1 - \frac{\cos2\widehat{A} +\cos2\widehat{B}}{2}

    = 1 - \cos\left( \widehat{A} +\widehat{B} ight).\cos\left( \widehat{A} - \widehat{B}ight)

    = 1 - \cos\widehat{C}.\cos\left(\widehat{A} - \widehat{B} ight) \geq 1

    Mặt khác \sqrt[2017]{\sin\widehat{C}}\leq \sqrt[2017]{1} = 1

    Do đó: sin^{2}\widehat{A} + sin^{2}\widehat{B} = \sqrt[2017]{\sin\widehat{C}} khi \left\{ \begin{matrix}\cos\widehat{C}.\cos\left( \widehat{A} - \widehat{B} ight) = 0 \\\sin\widehat{C} = 1 \\\end{matrix} ight.

    \Rightarrow \widehat{C} =\dfrac{\pi}{2}

    Vậy tam giác ABC là tam giác vuông tại \widehat{C}.

  • Câu 37: Nhận biết

    Cho 2\pi < \alpha < \frac{5\pi}{2}. Khẳng định nào sau đây đúng?

    Ta có 2\pi < \alpha < \frac{5\pi}{2}\overset{}{ightarrow}điểm cuối cung \alpha - \pi thuộc góc phần tư thứ I\overset{}{ightarrow}\left\{ \begin{matrix} \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight.\ .

  • Câu 38: Nhận biết

    Cho \Delta ABC có B = 60^{0},a = 8,c = 5. Độ dài cạnh b bằng:

    Ta có: b^{2} = a^{2} + c^{2} - 2ac\cos B = 8^{2} + 5^{2} - 2.8.5.cos60^{0} = 49 \Rightarrow b = 7.

  • Câu 39: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sin\alpha,\ cos\alpha cùng dấu?

    Điểm cuối của \alpha thuộc góc phần tư thứ nhất thì \sin\alpha > 0, \cos\alpha > 0.

    Điểm cuối của \alpha thuộc góc phần tư thứ nhất thì \sin\alpha < 0, \cos\alpha < 0.

    Vậy nếu \sin\alpha,\ cos\alpha cùng dấu thì điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc III.

  • Câu 40: Vận dụng

    Vào lúc 9 giờ sáng, hai vận động viên A và B xuất phát từ cùng một vị trí O. Vận động viên A chạy với vận tốc 13 km/h theo một góc so với hướng Bắc là 15°, vận động viên B chạy với vận tốc 12 km/h theo một góc so với hướng Bắc là 135° (hình vẽ).

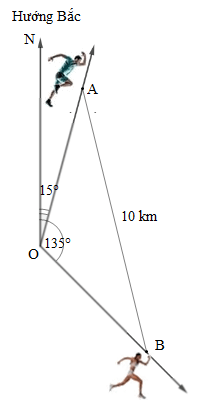
    Tính thời điểm hai vận động viên cách nhau 10km

    Tại thời điểm nào thì vận động viên A cách vận động viên B một khoảng 10 km (làm tròn kết quả đến phút)?

    Gọi khoảng thời gian kể từ khi bắt đầu chạy từ điểm O đến khi hai vận động viên cách nhau 10 km là x giờ

    Điều kiện: x > 0

    Khi đó đoạn đường mà vận động viên A chạy được là 13x (km)

    Đoạn đường mà vận động viên B chạy được là 12x (km)

    Ta có: \widehat {AOB} = {135^0} - {15^0} = {120^0}

    Áp dụng định lí cosin cho tam giác ABC ta có:

    \begin{matrix} A{B^2} = B{C^2} + A{C^2} - 2BC.AC.\cos \widehat {AOB} \hfill \\ \Leftrightarrow {10^2} = {\left( {13x} ight)^2} + {\left( {12x} ight)^2} - 2.13x.12x.\cos {120^0} \hfill \\ \Leftrightarrow {10^2} = 169{x^2} + 144{x^2} + 156{x^2} \hfill \\ \Leftrightarrow {x^2} = \dfrac{{100}}{{469}} \hfill \\ \Rightarrow x \approx 0,46 \hfill \\ \end{matrix}

    0,46 giờ ≈ 28 phút

    Do đó thời điểm mà hai vận động viên cách nhau 10 km là khoảng: 9 giờ 28 phút.

    Vậy vào khoảng 9 giờ 28 phút thì hai vận động viên sẽ cách nhau 10 km.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 3 Hệ thức lượng trong tam giác KNTT Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 15 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 3 Hệ thức lượng trong tam giác KNTT
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập