Lớp 12 Toán 12

Đề kiểm tra 45 phút Chương 3 Nguyên hàm - Tích phân và ứng dụng

Mô tả thêm: Đề kiểm tra 45 phút bao gồm các kiến thức Chương 3. Nguyên hàm - Tích phân được thay đổi liên tục giúp học sinh ôn tập kiến thức và kĩ năng giải bài tập Toán 12
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng

    Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD với A( - 2;3),B(3;6),C(3;0),D( - 2;0). Quay hình thang ABCD xung quanh trục Ox thì thể tích khối tròn xoay tạo thành bằng bao nhiêu??

    Phương trình các cạnh của hình thang là: \left\{ \begin{matrix} AD:x = - 2 \\ CD:y = 0 \\ BC:x = 3 \\ AB:3x - 5y + 21 = 0 \\ \end{matrix} ight.

    Ta thấy ABCD là hình thang vuông có CD:y = 0 nên khối tròn xoay cần tính là

    V = \pi\int_{- 2}^{3}{\frac{(3x + 21)^{2}}{25}dx} = 105\pi

  • Câu 2: Thông hiểu

    Một chất điểm chuyển động với gia tốc a(t) = 6t^{2} + 2t\left( m/s^{2} ight). Vận tốc ban đầu của chất điểm là 2(m/s). Hỏi vận tốc của chất điểm sau khi chuyển động với gia tốc đó được 2 giây bằng bao nhiêu?

    Ta có: v(2) - v(0) = \int_{0}^{2}{a(t)dt}

    \Rightarrow v(2) = \int_{0}^{2}{\left( 6t^{2} + 2t ight)dt} + v(0)

    \Rightarrow v(2) = \left. \ \left( 2t^{3} + t^{2} ight) ight|_{0}^{2} + 2 = 22

  • Câu 3: Thông hiểu

    Cho hình phẳng (H) như hình vẽ (phần tô đậm):

    Diện tích hình phẳng (H) là:

    Gọi S là diện tích hình phẳng (H) theo hình vẽ suy ra S = \int_{1}^{3}{x\ln xdx}

    Theo công thức tích phân từng phần:

    S = \left. \ \frac{x^{2}}{2}.\ln2ight|_{2}^{3} + \int_{1}^{3}{\frac{x}{2}dx} = \left. \frac{x^{2}}{2}.\ln2 ight|_{2}^{3} - \left. \ \frac{x^{2}}{4}ight|_{2}^{3} = \frac{9}{4}\ln3 - 2.

  • Câu 4: Vận dụng

    Xác định hàm số f(x) biết rằng f'\left( x ight) = x\sqrt {1 + {x^2}} ;3f\left( 0 ight) = 4

     \begin{matrix} f\left( x ight) = \int {f'\left( x ight)dx} \hfill \\ \Rightarrow f\left( x ight) = \int {x\sqrt {{x^2} + 1} dx} = \dfrac{1}{2}\int {{{\left( {{x^2} + 1} ight)}^{\frac{1}{2}}}d\left( {{x^2} + 1} ight) = \dfrac{{{{\left( {\sqrt {{x^2} + 1} } ight)}^3}}}{3} + C} \hfill \\ \end{matrix}

    Mà 3f\left( 0 ight) = 4 \Rightarrow 3\left[ {\frac{{{{\left( {\sqrt {{0^2} + 1} } ight)}^3}}}{3} + C} ight] = 4 \Rightarrow C = 1

    Vậy hàm số cần tìm là f\left( x ight) = \frac{{{{\left( {\sqrt {{x^2} + 1} } ight)}^3}}}{3} + 1

  • Câu 5: Nhận biết

    Tìm nguyên hàm của hàm số f(x) =\sin^{4}x\cos x??

    Đặt t = \sin x \Rightarrow dt = \cos xdx

    \int_{}^{}{\left( \sin^{4}x\cos xight)dx} = \int_{}^{}{t^{4}dt} = \frac{t^{5}}{5} + C =\frac{1}{5}\sin^{5}x + C

  • Câu 6: Vận dụng cao

    Cho hai quả bóng A, B đều chuyển động thẳng, di chuyển ngược chiều và va chạm với nhau. Sau mỗi va chạm, hai quả bóng nảy ngược lại một đoạn thì dừng hẳn. Tính khoảng cách giữa hai quả bóng sau khi dừng hẳn. Biết sau khi va chạm, quả bóng A này ngược lại với vận tốc {v_A}\left( t ight) = 8 - 2t\left( {m/s} ight) và quả bóng B nảy ngược lại với vận tốc {v_b}\left( t ight) = 12 - 4t\left( {m/s} ight).

    Thời gian quả bóng A chuyển động từ lúc va chạm đến khi dừng hẳn là:

    {v_A}\left( t ight) = 0 \Rightarrow 8 - 2t = 0 \Rightarrow t = 4\left( s ight)

    Quãng đường quả bóng A di chuyển được là: 

    {S_A} = \int\limits_0^4 {\left( {8 - 2t} ight)dt} = 16\left( m ight)

    Thời gian quả bóng B chuyển động từ lúc va chạm đến khi dừng hẳn là:

    {v_B}\left( t ight) = 0 \Rightarrow 12 - 4t = 0 \Rightarrow t = 3\left( s ight)

    Quãng đường quả bóng B di chuyển được là:

    {S_B} = \int\limits_0^3 {\left( {12 - 4t} ight)dt} = 18\left( m ight)

    Vậy khoảng cách hai quả bóng sau khi dừng hẳn là 

    S = {S_A} + {S_B} = 16 + 18 = 34\left( m ight)

  • Câu 7: Thông hiểu

    Biết rằng hàm số y = f(x) có f'(x) = 3x^{2} + 2x + m;f(2) = 1 và đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng - 5. Hàm số f(x) là:

    Theo lí thuyết \int_{}^{}{f'(x)dx = f(x) + C}

    Ta có: \int_{}^{}{f'(x)dx =}\int_{}^{}{\left( 3x^{2} + 2x + m ight)dx} = x^{3} + x^{2} + mx + C

    Khi đó f(x) có dạng f(x) = x^{3} + x^{2} + mx + C_{1}

    Theo đề ta có: \left\{ \begin{matrix} f(2) = 1 \\ f(0) = - 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 2^{3} + 2^{2} + 2m + C_{1} = 1 \\ C_{1} = - 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m = - 3 \\ C_{1} = - 5 \\ \end{matrix} ight.

    Vậy hàm số là f(x) = x^{3} + x^{2} - 3x - 5.

  • Câu 8: Vận dụng

    Cho là một nguyên hàm của hàm số f\left( x ight) = \frac{{\ln x}}{x}\sqrt {{{\ln }^2}x + 1} và F\left( 1 ight) = \frac{1}{3}. Tính {\left[ {F\left( e ight)} ight]^2}

     Cách 1: \int {f\left( x ight)} = \int {\frac{{\ln x}}{x}\sqrt {{{\ln }^2}x + 1} dx = \int {\sqrt {{{\ln }^2}x + 1} .} } \frac{{\ln x}}{x}dx

    Đặt \sqrt {{{\ln }^2}x + 1} = t

    \begin{matrix} \Rightarrow {\ln ^2}x + 1 = {t^2} \hfill \\ \Rightarrow 2\ln x.\dfrac{1}{x}dx = 2tdt \hfill \\ \Rightarrow \dfrac{{\ln x}}{x}dx = tdt \hfill \\ \end{matrix}

    Khi đó \int {f\left( x ight)} = \int {t.t.dt} = \int {{t^2}dt} = \frac{{{t^3}}}{3} + C

    => F\left( x ight) = \frac{1}{3}.{\left( {\sqrt {{{\ln }^2}x + 1} } ight)^3} + C

    Mặt khác F\left( 1 ight) = \frac{1}{3} \Leftrightarrow \frac{1}{3} = \frac{1}{3}.{\left( {\sqrt {{{\ln }^2}x + 1} } ight)^3} + C

    => C = 0

    => F\left( e ight) = \frac{1}{3}.{\left( {\sqrt {{{\ln }^2}e + 1} } ight)^3} = \frac{{2\sqrt 2 }}{3}

    => {\left[ {F\left( e ight)} ight]^2} = {\left( {\frac{{2\sqrt 2 }}{3}} ight)^2} = \frac{8}{9}

    Cách 2: F\left( e ight) - F\left( 1 ight) = \int\limits_1^e {\frac{{\ln x}}{x}.\sqrt {{{\ln }^2}x + 1} dx}. Sử dụng máy tính cầm tay để tính.

  • Câu 9: Thông hiểu

    Cho hàm số f(x) = \left\{ \begin{matrix} 2x\ \ \ \ \ \ \ \ khi\ x \geq 1 \\ 3x^{2} - 1\ \ khi\ x < 1 \\ \end{matrix} ight. có một nguyên hàm là F(x) thỏa mãn F(0) = 1 và F(x) liên túc trên \mathbb{R}. Giá trị biểu thức K = F( - 1) - F(2) bằng:

    Ta có: F(x) = \int_{}^{}{f(x)dx} = \left\{ \begin{matrix} x^{2} + C_{1}\ \ \ \ \ \ \ \ khi\ x \geq 1 \\ x^{3} - x + C_{2}\ \ khi\ x < 1 \\ \end{matrix} ight.

    F(0) = 1 \Rightarrow C_{2} = 1

    Vì hàm số F(x) liên tục trên \mathbb{R} nên liên tục tại x = 1 tức là

    \lim_{x ightarrow 1^{+}}F(x) = \lim_{x ightarrow 1^{-}}F(x) = F(1)

    \Leftrightarrow 1 + C_{1} = C_{2} \Leftrightarrow C_{1} = 0

    Do đó F(x) = \left\{ \begin{matrix} x^{2}\ \ \ \ \ \ \ \ khi\ x \geq 1 \\ x^{3} - x + 1\ \ khi\ x < 1 \\ \end{matrix} ight.

    K = F( - 1) - F(2) = ( - 1 + 1 + 1) + \left( 2^{2} ight) = 5

  • Câu 10: Vận dụng

    Tìm tổng các nghiệm của phương trình F(x) = x, biết F(x) là một nguyên hàm của hàm số f\left( x ight) = \frac{x}{{\sqrt {8 - {x^2}} }} thỏa mãn F(2) = 0 

    \begin{matrix} F\left( x ight) = \int {f\left( x ight)dx} \hfill \\ = \int {\dfrac{x}{{\sqrt {8 - {x^2}} }}dx} = \dfrac{1}{2}\int {d\frac{x}{{\sqrt {8 - {x^2}} }}d\left( {8 - {x^2}} ight)} \hfill \\ \Rightarrow F\left( x ight) = - \sqrt {8 - {x^2}} + C \hfill \\ \end{matrix}

    Ta có: F(2) = 0 => C = 2

    => F\left( x ight) = - \sqrt {8 - {x^2}} + 2

    Xét phương trình F(x) = x ta có:

    \begin{matrix} F\left( x ight) = x \hfill \\ \Leftrightarrow - \sqrt {8 - {x^2}} + 2 = x \hfill \\ \Leftrightarrow \sqrt {8 - {x^2}} = 2 - x \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2 - x \geqslant 0} \\ {8 - {x^2} = {{\left( {2 - x} ight)}^2}} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 2} \\ {{x^2} - 2x + 2 = 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 2} \\ {x = 1 \pm \sqrt 3 } \end{array}} ight. \Leftrightarrow x = 1 - \sqrt 3 \hfill \\ \end{matrix}

    Vậy tổng các nghiệm của phương trình đã cho bằng x = 1 - \sqrt 3

  • Câu 11: Vận dụng cao

    Cho hàm số y = f(x) xác định trên \mathbb{R}\backslash \left\{ 0 ight\} thỏa mãn 2xf\left( x ight) + {x^2}f'\left( x ight) = 1;f\left( 1 ight) = 0. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại giao điểm với trục hoành là:

    Ta có:

    \begin{matrix} 2xf\left( x ight) + {x^2}f'\left( x ight) = 1 \hfill \\ \Leftrightarrow \left( {{x^2}} ight)'.f\left( x ight) + {x^2}.f'\left( x ight) = 1 \hfill \\ \Leftrightarrow \left[ {{x^2}f\left( x ight)} ight]' = 1 \hfill \\ \end{matrix}

    Lấy nguyên hàm hai vế ta được:

    \begin{matrix} \int {\left[ {{x^2}f\left( x ight)} ight]'dx} = \int {1.dx} \hfill \\ \Leftrightarrow {x^2}f\left( x ight) = x + C \hfill \\ \end{matrix}

    Ta có:

    \begin{matrix} f\left( 1 ight) = 0 \Rightarrow 1.f\left( 1 ight) = 1 + C \Rightarrow C = - 1 \hfill \\ \Rightarrow {x^2}f\left( x ight) = x - 1 \Rightarrow f\left( x ight) = \dfrac{{x - 1}}{{{x^2}}} \hfill \\ \end{matrix}

    Xét phương trình hoành độ giao điểm với trục hoành ta có:

    \frac{{x - 1}}{{{x^2}}} = 0 \Rightarrow x = 1\left( {tm} ight)

    Ta lại có: f'\left( x ight) = \frac{{2 - x}}{{{x^2}}} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {f'\left( 1 ight) = 1} \\ {f\left( 1 ight) = 0} \end{array}} ight.

    Phương trình tiếp tuyến tại giao điểm với trục hoành là:

    y = f'\left( 1 ight)\left( {x - 1} ight) + f\left( 1 ight) \Rightarrow y = x - 1

  • Câu 12: Nhận biết

    Hàm số nào sau đây là một nguyên hàm của hàm số f(x) = 25^{x}?

    Vì: \left( \frac{25^{x}}{ln25} ight)' = \frac{1}{ln25}.25^{x}.ln25 = 25^{x}

  • Câu 13: Nhận biết

    Tìm nguyên hàm của hàm số f\left( x ight) = \cos 3x

     Ta có: \int {\cos 3xdx} = \frac{{\sin 3x}}{3} + C

  • Câu 14: Nhận biết

    Tìm nguyên hàm của hàm số f\left( x ight) = 3x + \cos 3x

     Ta có: \int {\left( {3x + \cos 3x} ight)dx = \frac{{3{x^2}}}{2} + \frac{{\sin 3x}}{3} + C}

  • Câu 15: Vận dụng cao

    Cho hàm số y = f(x) có đạo hàm dương và liên tục trên \lbrack 0;1brack thỏa mãn f(0) = 1 và 5\int_{0}^{1}{\left\{ f'(x)\left\lbrack f(x) ightbrack^{2} + \frac{1}{25} ight\} dx} \leq 2\int_{0}^{1}{\left\lbrack \sqrt{f'(x)}.f(x) ightbrack dx}. Tích phân \int_{0}^{1}{\left\lbrack f(x) ightbrack^{3}dx} là:

    5\int_{0}^{1}\mspace{2mu}\left\lbrack f^{'}(x)\lbrack f(x)brack^{2} + \frac{1}{25} ightbrack dx \leqslant 2\int_{0}^{1}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dx

    \Leftrightarrow5\int_{0}^{1}\mspace{2mu} f^{'}(x)\lbrack f(x)brack^{2}dx+ \frac{1}{5} \leqslant2\int_{0}^{1}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dx

    Áp dụng BĐT Cauchy-Schwarz:

    \Rightarrow \left(\int_{0}^{1}\mspace{2mu}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dxight)^{2} \leqslant \int_{0}^{1}\mspace{2mu}\mspace{2mu}dx\cdot \int_{0}^{1}\mspace{2mu}\mspace{2mu} f^{'}(x)\lbrack f(x)brack^{2}dx

    \Rightarrow 5\left(\int_{0}^{1}\mspace{2mu}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dxight)^{2} + \frac{1}{5} \leqslant2\int_{0}^{2}\mspace{2mu}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dx

    \Leftrightarrow 5\left( \int_{0}^{1}\mspace{2mu}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dx - \frac{1}{5} ight)^{2} \leqslant 0 \Leftrightarrow \int_{0}^{1}\mspace{2mu}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dx = \frac{1}{5}.

    Dấu "=" xảy ra khi chỉ khi \left\{\begin{matrix}\int_{0}^{1}\mspace{2mu}\mspace{2mu}\sqrt{f^{'}(x)}f(x)dx =\dfrac{1}{5} \Rightarrow k = \dfrac{1}{5} \\\sqrt{f^{'}(x)}f(x) = k \\\end{matrix} ight.

    \Rightarrow \int_{}^{}\ f^{'}(x)f^{2}(x)dx = \int_{}^{}\ \frac{1}{25}dx = \frac{1}{25}x + C

    \Rightarrow \frac{\left\lbrack f(x) ightbrack^{3}}{3} = \frac{1}{25}x + C \Leftrightarrow f(x) = \sqrt[3]{\frac{3}{25}x + 3C}

    f(0) = 1 \Rightarrow 3C = 1 \Rightarrow f(x) = \sqrt[3]{\frac{3}{25}x + 1}

    \Rightarrow \int_{0}^{1}{\left\lbrack f(x) ightbrack^{3}dx} = \int_{0}^{1}{\left( \frac{3}{25}x + 1 ight)dx} = \frac{53}{50}

  • Câu 16: Thông hiểu

    Biết rằng f'(x) = x\sqrt{1 + x^{2}} và 3f(0) = 4. Tìm hàm số f(x)?

    Ta có: f(x) = \int_{}^{}{f'(x)dx} = \int_{}^{}{x\sqrt{1 + x^{2}}dx}

    = \frac{1}{2}\int_{}^{}{\left( 1 + x^{2} ight)^{\frac{1}{2}}d\left( 1 + x^{2} ight)} = \frac{\left( \sqrt{1 + x^{2}} ight)^{3}}{3} + C

    Mà 3f(0) = 4 \Leftrightarrow 3\frac{\left( \sqrt{1 + 0^{2}} ight)^{3}}{3} + 3C = 4 \Leftrightarrow C = 1

    Vậy f(x) = \frac{\left( \sqrt{1 + x^{2}} ight)^{3}}{3} + 1

  • Câu 17: Thông hiểu

    Hàm số F\left( x ight) = 2\sin x - 3\cos x là một nguyên hàm của hàm số nào sau đây?

     F'\left( x ight) = f\left( x ight) = 2\cos x + 3\sin x

  • Câu 18: Thông hiểu

    Cho hàm số F(x) là một nguyên hàm của f(x) = \frac{1}{x - 1} trên khoảng (1; + \infty) thỏa mãn F(e + 1) = 4. Xác định công thức F(x)?

    Ta có: F(x) = \int_{}^{}\frac{dx}{x - 1} = \int_{}^{}\frac{d(x - 1)}{x - 1} = \ln|x - 1| + C = \ln(x - 1) + C (vì (1; + \infty))

    Mà F(e + 1) = 4 \Leftrightarrow \ln(e + 1 - 1) + C = 4 \Rightarrow C = 3

    Vậy F(x) = \ln(x - 1) + 3.

  • Câu 19: Thông hiểu

    Cho giá trị của tích phân {I_1} = \int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{3}} {\left( {\sin 2x + \cos x} ight)dx} = a, {I_2} = \int\limits_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {\left( {\cos 2x + \sin x} ight)dx} = b. Giá trị của a + b là:

    Ta có: 

    {I_1} = \int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{3}} {\left( {\sin 2x + \cos x} ight)dx} = \left. {\left( { - \dfrac{1}{2}\cos 2x + \sin x} ight)} ight|_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{3}}

    = \dfrac{3}{4} + \dfrac{{\sqrt 3 }}{2} \Rightarrow a = \dfrac{3}{4} + \dfrac{{\sqrt 3 }}{2}

    {I_2} = \int\limits_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {\left( {\cos 2x + \sin x} ight)dx} = \left. {\left( {\frac{1}{2}\sin 2x - \cos x} ight)} ight|_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} = \frac{{\sqrt 3 }}{2} \Rightarrow b = \frac{{\sqrt 3 }}{2}

    \Rightarrow P = a + b = \frac{3}{4} + \sqrt 3

    Ngoài ra ta có thể sử dụng máy tính cầm tay nhập trực tiếp biểu thức và tính ra kết quả.

  • Câu 20: Nhận biết

    Tìm nguyên hàm của hàm số f(x) = \frac{x - 1}{x^{2}}?

    Ta có: f(x) = \frac{x - 1}{x^{2}} = \frac{1}{x} - \frac{1}{x^{2}} \Rightarrow F(x) = \ln|x| + \frac{1}{x} + C

  • Câu 21: Thông hiểu

    Thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường y = x\sqrt {\ln \left( {1 + {x^3}} ight)} ;y = 0;x = 1, khi xoay quanh trục Ox.

     Phương trình hoành độ giao điểm là: x\sqrt {\ln \left( {1 + {x^3}} ight)} = 0 \Leftrightarrow x = 0

    Gọi là thể tích khối tròn xoay cần tìm ta có: V= \pi \int\limits_0^1 {{x^2}\ln \left( {1 + {x^3}} ight)dx}

    Đặt \left\{ {\begin{array}{*{20}{c}} {u = \ln \left( {1 + {x^3}} ight)} \\ {dv = {x^2}dx} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {du = \dfrac{{3{x^2}}}{{1 + {x^3}}}dx} \\ {v = \dfrac{{{x^3} + 1}}{3}} \end{array}} ight.

    \begin{matrix} \Rightarrow V = \pi \left\{ {\left[ {\dfrac{{{x^3} + 1}}{3}\ln \left( {1 + {x^3}} ight)} ight]_0^1 - \int\limits_0^1 {{x^2}dx} } ight\} \hfill \\ \Rightarrow V = \pi \left( {\dfrac{{2\ln 2}}{3} - \dfrac{1}{3}} ight) \hfill \\ \end{matrix}

  • Câu 22: Nhận biết

    Cho hàm số f(x) liên tục trên đoạn \lbrack - 5;3brack và F(x) là một nguyên hàm của f(x). Biết rằng F( - 5) = 3;F(3) = \frac{15}{7}. Xác định tích phân I = \int_{- 5}^{3}{\left\lbrack 7f(x) - x ightbrack dx}?

    Ta có: I = \int_{- 5}^{3}{\left\lbrack 7f(x) - x ightbrack dx} = \left. \ \left( 7F(x) ight) ight|_{- 5}^{3} - \left. \ \frac{x^{2}}{2} ight|_{- 5}^{3} = 2.

  • Câu 23: Thông hiểu

    Cho hàm số f(x) xác định trên \mathbb{R}\left\{ 1 ight\}thỏa mãn f'(x) = \frac{1}{x - 1}; f(0) = 2017;f(2) = 2018. Tính T = f(3) - f( - 1)?

    Trên khoảng (1; + \infty) ta có: \int_{}^{}{f'(x)dx} = \int_{}^{}{\frac{1}{x - 1}dx} = \ln(x - 1) + C_{1}

    \Rightarrow f(x) = \ln(x - 1) + C_{1}

    Mà f(2) = 2018 \Rightarrow C_{1} = 2018

    Trên khoảng ( - \infty;1) ta có: \int_{}^{}{f'(x)dx} = \int_{}^{}{\frac{1}{x - 1}dx} = \ln(1 - x) + C_{2}

    \Rightarrow f(x) = \ln(1 - x) + C_{2}

    Mà f(0) = 2017 \Rightarrow C_{2} = 2017

    Vậy f(x) = \left\{ \begin{matrix} \ln(x - 1) + 2018\ \ \ khi\ x\ > \ 1 \\ \ln(1 - x) + 2017\ \ \ khi\ x\ < \ 1 \\ \end{matrix} ight.

    \Rightarrow T = f(3) - f( - 1) = 1.

  • Câu 24: Thông hiểu

    Biết \int_{1}^{2}{\left\lbrack 4f(x) - 2x ightbrack dx} = 1. Khi đó \int_{1}^{2}{f(x)dx} bằng:

    Ta có:

    \int_{1}^{2}{\left\lbrack 4f(x) - 2x ightbrack dx} = 1 \Leftrightarrow 4\int_{1}^{2}{f(x)dx} - 2\int_{1}^{2}{xdx} = 1

    \Leftrightarrow 4\int_{1}^{2}{f(x)dx} - 2\left. \ .x^{2} ight|_{1}^{2} = 1 \Leftrightarrow 4\int_{1}^{2}{f(x)dx} = 4 \Leftrightarrow \int_{1}^{2}{f(x)dx} = 1

  • Câu 25: Vận dụng

    Tích phân I = \int\limits_0^1 {\frac{{2ax}}{{x + 1}}dx} = \ln 2. Giá trị của a là:

    Ta có:

    I = \int\limits_0^1 {\frac{{2ax}}{{x + 1}}dx} = 2a\int\limits_0^1 {\left( {1 - \frac{1}{{x + 1}}} ight)dx} = 2a\left. {\left( {x - \ln \left| {x + 1} ight|} ight)} ight|_0^1 = 2a\left( {1 - \ln 2} ight)

    Mà I = \ln 2 \Leftrightarrow 2a\left( {1 - \ln 2} ight) = \ln 2 \Leftrightarrow a = \frac{{\ln 2}}{{2 - 2\ln 2}}

  • Câu 26: Thông hiểu

    Một bình cắm hoa dạng khối tròn xoay, biết đáy bình và miệng bình có đường kính lần lượt là 2dm và 4dm. Mặt xung quanh của bình là một phần của mặt tròn xoay có đường sinh là đồ thị hàm số y = \sqrt{x - 1}. Tính thể tích bình cắm hoa?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Một bình cắm hoa dạng khối tròn xoay, biết đáy bình và miệng bình có đường kính lần lượt là 2dm và 4dm. Mặt xung quanh của bình là một phần của mặt tròn xoay có đường sinh là đồ thị hàm số y = \sqrt{x - 1}. Tính thể tích bình cắm hoa?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 27: Vận dụng

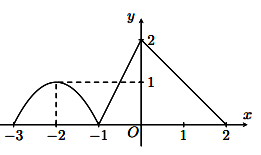
    Cho hàm số f(x) xác định trên \mathbb{R}\backslash \left\{ 1 ight\} thỏa mãn f'\left( x ight) = \frac{2}{{x - 1}};f\left( 0 ight) = 3;f\left( 2 ight) = 4. Tính giá trị của biểu thức  N = f\left( { - 2} ight) + f\left( 5 ight)

     

    f\left( x ight) = \int {f'\left( x ight)dx} = \int {\frac{2}{{x - 1}}dx} = \ln \left| {2x - 1} ight| + C

    => f\left( x ight) = \left\{ {\begin{array}{*{20}{c}} {2\ln \left( {x - 1} ight) + {C_1}{\text{ khi x > }}1} \\ {2\ln \left| {1 - x} ight| + {C_2}{\text{ khi x < }}1} \end{array}} ight.

    Theo bài ra ta có: \left\{ {\begin{array}{*{20}{c}} {f\left( 0 ight) = 3 \Rightarrow \ln \left( {1 - 0} ight) + {C_2} = 3} \\ {f\left( 2 ight) = 4 \Rightarrow \ln \left( {2 - 1} ight) + {C_1} = 4} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{C_2} = 3} \\ {{C_1} = 4} \end{array}} ight.

    => f\left( x ight) = \left\{ {\begin{array}{*{20}{c}} {2\ln \left( {x - 1} ight) + 4{\text{ khi x > }}1} \\ {2\ln \left| {1 - x} ight| + 3{\text{ khi x < }}1} \end{array}} ight.

    => N = f\left( { - 2} ight) + f\left( 5 ight) = \left\{ {2\ln \left[ {1 - \left( { - 2} ight)} ight] + 3} ight\} + \left\{ {2\ln \left( {5 - 1} ight) + 4} ight\}

    = 2\ln 3 + 2\ln 4 + 7

  • Câu 28: Thông hiểu

    Xác định nguyên hàm F(x) của hàm số f(x) = \frac{x^{3} + 3x^{2} + 3x - 1}{x^{2} + 2x + 1}?

    Ta có:

    f(x) = \frac{x^{3} + 3x^{2} + 3x - 1}{x^{2} + 2x + 1} = \frac{(x + 1)^{3} - 2}{(x + 1)^{2}} = x + 1 - \frac{2}{(x + 1)^{2}}

    \Rightarrow F(x) = \frac{x^{2}}{2} + x + \frac{2}{x + 1} + C

  • Câu 29: Vận dụng

    Cho hàm số f(x) liên tục và có đạo hàm trên \left( 0;\frac{\pi}{2} ight) thỏa mãn f(x) + \tan xf'(x) = \frac{x}{\cos^{3}x}. Biết rằng \sqrt{3}f\left( \frac{\pi}{3} ight) - f\left( \frac{\pi}{6} ight) = a\pi\sqrt{3} + bln3 trong đó a;b\mathbb{\in R}. Kết luận nào sau đây đúng?

    Ta có: f(x) + \tan xf'(x) =\frac{x}{\cos^{3}x}

    \Leftrightarrow \cos xf(x) + \sin xf'(x) = \frac{x}{\cos^{2}x}

    \Leftrightarrow \left\lbrack \sin xf(x)ightbrack' = \frac{x}{\cos^{2}x}

    \Rightarrow \int_{}^{}{\left\lbrack \sin xf(x) ightbrack'dx} =\int_{}^{}{\frac{x}{\cos^{2}x}dx}

    \Rightarrow \sin xf(x) =\int_{}^{}{\frac{x}{\cos^{2}x}dx}.

    Tính I = \int_{}^{}{\frac{x}{cos^{2}x}dx}. Đặt \left\{ \begin{matrix}u = x \\dv = \dfrac{dx}{\cos^{2}x} \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}du = dx \\v = \tan x \\\end{matrix} ight. khi đó:

    I = x\tan x - \int_{}^{}{\tan xdx} = x\tan x - \int_{}^{}\frac{d\left( \cos x ight)}{\cos x}

    = x\tan x + \ln\left| \cos x ight|

    \Rightarrow f(x) = \frac{x\tan x + \ln\left| \cos x ight|}{\sin x} = \frac{x}{\cos x} + \frac{\ln\left| \cos x ight|}{\sin x}

    Theo bài ra ta có:

    \Rightarrow \sqrt{3}f\left(\frac{\pi}{3} ight) - f\left( \frac{\pi}{6} ight) = \sqrt{3}\left(\frac{2\pi}{3} - \dfrac{2\ln2}{\sqrt{3}} ight)- \left(\frac{\pi\sqrt{3}}{9} + 2\ln\dfrac{\sqrt{3}}{2} ight) =\dfrac{5\pi\sqrt{3}}{9}\ln3

    \Rightarrow \left\{ \begin{matrix}a = \dfrac{5}{9} \\b = - 1 \\\end{matrix} ight.\ \Rightarrow a + b = - \frac{4}{9}

  • Câu 30: Thông hiểu

    Gọi F(x) là một nguyên hàm của hàm số f(x) = e^{x}, thỏa mãn F(0) = 2020. Tính giá trị biểu thức T = F(0) + F(1) + ... + F(2018) + F(2019)?

    Ta có: \int_{}^{}{f(x)dx} = \int_{}^{}{e^{x}dx} = e^{x} + C

    F(x) là một nguyên hàm của hàm số f(x) = e^{x}, ta có: F(x) = e^{x} + C mà F(0) = 2020

    \Rightarrow C = 2019 \Rightarrow F(x) = e^{x} + 2019

    T = F(0) + F(1) + ... + F(2018) + F(2019)

    T = 1 + e + e^{2} + .... + e^{2018} + e^{2019} + 2019.2020

    T = \frac{e^{2020} - 1}{e - 1} + 2019.2020.

  • Câu 31: Vận dụng

    Cho đường cong (C) y = {x^3}. Xét điểm A có hoành độ dương thuộc (C), tiếp tuyến của (C) tại A tạo với (C) một hình phẳng có diện tích bằng 27. Hoành độ điểm A thuộc khoảng nào dưới đây?

    Ta có: y' = 3{x^2}

    Ta có: A \in \left( C ight) \Rightarrow A\left( {a;{a^3}} ight);a > 0

    Phương trình tiếp tuyến d của (C) tại A là d:y = 3{a^2}\left( {x - a} ight) + {a^3}

    Ta có phương trình hoành độ giao điểm d và (C) là:

    \begin{matrix} {x^3} = 3{a^2}\left( {x - a} ight) + {a^3} \hfill \\ \Leftrightarrow {\left( {x - a} ight)^2}\left( {x + 2a} ight) = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = a} \\ {x = - 2a} \end{array}} ight. \hfill \\ \end{matrix}

    Gọi S là diện tích của hình phẳng giới hạn bởi tiếp tuyến d và (C).

    Ta có:

    \begin{matrix} S = 27 \hfill \\ \Rightarrow \int\limits_{ - 2a}^a {\left| {{x^3} - 3{a^2}\left( {x - a} ight) - {a^3}} ight|dx = 27} \hfill \\ \Rightarrow \left| {\int\limits_{ - 2a}^a {\left( {{x^3} - 3{a^2}\left( {x - a} ight) - {a^3}} ight)dx} } ight| = 27 \hfill \\ \Rightarrow \left| {\left. {\left( {\dfrac{{{x^4}}}{4} - \dfrac{{3{a^2}{x^2}}}{2} + 2{a^3}x} ight)} ight|_{ - 2a}^a} ight| = 27 \hfill \\ \Leftrightarrow \dfrac{{27}}{4}{a^4} = 27 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {a = \sqrt 2 \left( {tm} ight)} \\ {a = - \sqrt 2 \left( {ktm} ight)} \end{array}} ight. \Rightarrow a = \sqrt 2 \hfill \\ \end{matrix}

  • Câu 32: Thông hiểu

    Cho \int_{0}^{\frac{\pi}{2}}{f(x)dx = 6}. Tính I =\int_{0}^{\frac{\pi}{2}}{\lbrack 3f(x) - 2sinxbrack dx}.

    Ta có:

    I = \int_{0}^{\frac{\pi}{2}}{\lbrack 3f(x) - 2sinxbrack dx}

    = 3\int_{0}^{\frac{\pi}{2}}{f(x)dx} - 2\int_{0}^{\frac{\pi}{2}}{\sin xdx} = 3.6 - 2 = 16.

  • Câu 33: Nhận biết

    Tích phân I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} ight)dx} có giá trị là:

     Tích phân I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} ight)dx} có giá trị là:

    I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} ight)dx} = \left. {\left( { - \frac{1}{x} + {x^2}} ight)} ight|_1^2 = \frac{7}{2}

    Ngoài ra ta có thể sử dụng máy tính cầm tay nhập trực tiếp biểu thức và tính ra kết quả.

  • Câu 34: Vận dụng cao

    Cho hàm số f\left( x ight) = \left( {{x^2} - 1} ight){e^{{x^3} - 3x}} biết rằng đồ thị hàm số F(x) có điểm cực tiểu nằm trên trục hoành. Chọn công thức đúng của 3e^2F(x)?

     Ta có:

    F\left( x ight) = \int {\left( {{x^2} - 1} ight){e^{{x^3} - 3x}}dx = \frac{1}{3}\int {{e^{{x^3} - 3x}}d\left( {{x^3} - 3x} ight) = \frac{1}{3}{e^{{x^3} - 3x}} + C} }

    Mà F'\left( x ight) = f\left( x ight) = \left( {{x^2} - 1} ight){e^{{x^3} - 3x}} = 0 \Rightarrow x = \pm 1

    \begin{matrix} F''\left( x ight) = 2x.{e^{{x^3} - 3x}} + \left( {{x^2} - 1} ight)\left( {3{x^2} - 3} ight){e^{{x^3} - 3x}} \hfill \\ F''\left( 1 ight) > 0;F''\left( { - 1} ight) < 0 \hfill \\ \end{matrix}

    Do đó hàm số đạt cực tiểu tại x = 1

    Mặt khác đồ thị hàm số có cực tiểu nằm trên trục hoành nên ta có điểm cực tiểu là A(0; 1)

    => F\left( 1 ight) = 0 \Rightarrow \frac{1}{3}{e^{ - 2}} + C = 0 \Rightarrow C = - \frac{1}{{3{e^2}}}

    => F\left( x ight) = \frac{{{e^{{x^3} - 3x + 2}} - 1}}{{3{e^2}}} Hay  3e^2F(x) = e^{{x^3} - 3x + 2} - 1

  • Câu 35: Thông hiểu

    Biết rằng F(x) liên tục trên \mathbb{R} là một nguyên hàm của hàm số f(x) = \left\{ \begin{matrix} 3x^{2} + 2\ \ \ khi\ x \geq 2 \\ 4x^{3} - 18\ \ \ khi\ x < 2 \\ \end{matrix} ight.. Giá trị biểu thức F( - 1) - F(3) bằng:

    Ta có: F(x) = \int_{}^{}{f(x)dx} = \left\{ \begin{matrix} x^{3} + 2x + C_{1}\ \ \ khi\ x \geq 2 \\ x^{4} - 18x + C_{2}\ \ \ khi\ x < 2 \\ \end{matrix} ight.

    Vì hàm số F(x) liên tục trên \mathbb{R} nên liên tục tại x = 2 tức là

    \lim_{x ightarrow 2^{+}}F(x) = \lim_{x ightarrow 2^{-}}F(x) = F(2)

    \Leftrightarrow 12 + C_{1} = - 20 + C_{2} \Leftrightarrow C_{1} - C_{2} = - 32

    Do đó

    F( - 1) - F(3) = \left( 1 + 18 + C_{2} ight) - \left( 27 + 6 + C_{1} ight)

    = - 14 - \left( C_{1} - C_{2} ight) = - 14 + 32 = 18

  • Câu 36: Nhận biết

    Tính diện tích hình phẳng giới hạn bởi các đường thẳng y = \cos x;Ox;x = - \frac{\pi}{2};x = \frac{\pi}{2}?

    Hình vẽ minh họa

    Ta có: \cos x = 0 \Rightarrow x = \frac{\pi}{2} + k\pi;k\mathbb{\in Z}

    Từ đó ta thấy phương trình hoành độ không có nghiệm nào thuộc khoảng \left( - \frac{\pi}{2};\frac{\pi}{2} ight)

    Diện tích hình giới hạn là S = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\left| \cos x ight|dx} = \left| \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\cos xdx} ight| = \left| \left. \ \sin x ight|_{- \frac{\pi}{2}}^{\frac{\pi}{2}} ight| = 2

  • Câu 37: Vận dụng cao

    Cho hàm số f(x) liên tục trên đoạn \lbrack - 6;5brack có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ:

    Tính giá trị I = \int_{- 6}^{5}{\left\lbrack f(x) + 2 ightbrack dx}?

    Hình vẽ minh họa

    Dựa vào đồ thị ta có: A( - 6; - 1),B( - 2;1) suy ra phương trình đường thẳng AB:y = \frac{1}{2}x + 2

    \Rightarrow I_{1} = \int_{0}^{- 2}{\left\lbrack \frac{1}{2}x + 2 + 2 ightbrack dx} = 8

    Phương trình đường tròn (C): x^{2} + (y - 1)^{2} = 4 \Rightarrow y = 1 + \sqrt{4 - x^{2}}

    \Rightarrow I_{2} = \int_{- 2}^{2}{\left\lbrack 1 + \sqrt{4 - x^{2}} + 2 ightbrack dx} = 12 + 2\pi

    Điểm C(2;1),D(5;3) nên phương trình đường thẳng CD là: y = \frac{2}{3}x - \frac{1}{3}

    \Rightarrow I_{3} = \int_{2}^{5}{\left\lbrack \frac{2}{3}x - \frac{1}{3} + 2 ightbrack dx} = 12

    Vậy I = I_{1} + I_{2} + I_{3} = 32 + 2\pi

  • Câu 38: Nhận biết

    Giá trị của tích phân I = \int\limits_0^1 {\frac{x}{{x + 1}}} dx = a. Biểu thức có giá trị P = 2a - 1 là:

    Giá trị của tích phân I = \int\limits_0^1 {\frac{x}{{x + 1}}} dx = a. Biểu thức P = 2a - 1 có giá trị là:

    Ta có:

    \begin{matrix} I = \int\limits_0^1 {\dfrac{x}{{x + 1}}} dx \hfill \\ = \int\limits_0^1 {\left( {1 - \dfrac{1}{{x + 1}}} ight)dx} \hfill \\ = \left. {\left( {x - \ln \left| {x + 1} ight|} ight)} ight|_0^1 \hfill \\ = 1 - \ln 2 \hfill \\ \Rightarrow a = 1 - \ln 2 \hfill \\ \Rightarrow P = 2a - 1 = 1 - 2\ln 2 \hfill \\ \end{matrix}

     

  • Câu 39: Thông hiểu

    Diện tích S của hình phẳng giới hạn bởi đường cong y = - x^{3} + 3x^{2} - 2, trục hoành và hai đường thẳng x = 0;x = 2 là

    Phương trình hoành độ giao điểm

    - x^{3} + 3x^{2} - 2 = 0 \Leftrightarrow (1 - x)\left( x^{2} - 2x - 2 ight) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 1 + \sqrt{3} \\ x = 1 - \sqrt{3} \\ \end{matrix} ight.

    Khi đó:

    S = \int_{0}^{2}{\left| - x^{3} + 3x^{2} - 2 ight|dx}

    = \int_{0}^{1}{\left| - x^{3} + 3x^{2} - 2 ight|dx} + \int_{1}^{2}{\left| - x^{3} + 3x^{2} - 2 ight|dx}

    = \left| \int_{0}^{1}{\left( - x^{3} + 3x^{2} - 2 ight)dx} ight| + \left| \int_{1}^{2}{\left( - x^{3} + 3x^{2} - 2 ight)dx} ight|

    = \left| \left. \ \left( - \frac{x^{4}}{4} + x^{3} - 2x ight) ight|_{0}^{1} ight| + \left| \left. \ \left( - \frac{x^{4}}{4} + x^{3} - 2x ight) ight|_{1}^{2} ight|

    = \frac{5}{2}

  • Câu 40: Nhận biết

    Cho hàm số f(x) liên tục trên đoạn \left\lbrack 0;\frac{\pi}{2} ightbrack và \int_{0}^{\frac{\pi}{2}}{f(x)dx} = 5. Tính tích phân I = \int_{0}^{\frac{\pi}{2}}{\left\lbrack f(x) + 2sinx ightbrack dx}?

    Ta có:

    I =\int_{0}^{\frac{\pi}{2}}{\left\lbrack f(x) + 2\sin x ightbrack dx} =\int_{0}^{\frac{\pi}{2}}{f(x)dx} +\int_{0}^{\frac{\pi}{2}}{2\sin xdx}

    = 5 - \left. \ 2\cos xight|_{0}^{\frac{\pi}{2}} = 7

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 3 Nguyên hàm - Tích phân và ứng dụng Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 42 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 3 Nguyên hàm - Tích phân và ứng dụng
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập