Lớp 10 Toán 10 - Chân trời sáng tạo

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác Sách CTST

Mô tả thêm: Đề kiểm tra 1 tiết Toán 10 Hệ thức lượng trong tam giác gồm 40 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Chân trời sáng tạo.
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Một tam giác có ba cạnh là 52,\ 56,\ 60. Bán kính đường tròn ngoại tiếp tam giác đó là:

    Ta có: p = \frac{52 + 56 + 60}{2} = 84.

    Áp dụng hệ thức Hê - rông ta có:

    S = \sqrt{84 \cdot (84 - 52) \cdot (84 - 56) \cdot (84 - 60)} = 1344.

    Mặt khác S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S\ } = \frac{52.56.60}{4.1344} = 32.5

  • Câu 2: Vận dụng

    Tính giá trị của \cos\left\lbrack \frac{\pi}{4} + (2k + 1)\pi ightbrack.

    Ta có \cos\left\lbrack \frac{\pi}{4} + (2k + 1)\pi ightbrack = \cos\left( \frac{5\pi}{4} + 2k\pi ight) = \cos\frac{5\pi}{4}

    = \cos\left( \pi + \frac{\pi}{4} ight) = - \cos\frac{\pi}{4} = - \frac{\sqrt{2}}{2}.

  • Câu 3: Vận dụng

    Cho góc \alpha thỏa mãn \cot\alpha = \frac{1}{3}. Tính P = \frac{3sin\alpha + 4cos\alpha}{2sin\alpha - 5cos\alpha}.

    Chia cả tử và mẫu của P cho \sin\alpha ta được P = \frac{3 + 4cot\alpha}{2 - 5cot\alpha} = \frac{3 + 4.\frac{1}{3}}{2 - 5.\frac{1}{3}} = 13.

  • Câu 4: Nhận biết

    Cho biết \tan\alpha = \frac{1}{2}. Tính \cot\alpha.

    Ta có: \tan\alpha.cot\alpha = 1 \Rightarrow \cot\alpha = \frac{1}{\tan\alpha} = \frac{1}{\frac{1}{2}} = 2.

  • Câu 5: Nhận biết

    Tam giác ABC có \widehat{B} = 60{^\circ},\ \ \widehat{C} = 45{^\circ} và AB = 5. Tính độ dài cạnh AC.

    Theo định lí hàm sin, ta có \frac{AB}{\sin\widehat{C}} = \frac{AC}{\sin\widehat{B}} \Leftrightarrow \frac{5}{sin45{^\circ}} = \frac{AC}{sin60{^\circ}} \Rightarrow AC = \frac{5\sqrt{6}}{2}.

  • Câu 6: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.

    Điểm cuối của \alpha thuộc góc phần tư thứ nhất ightarrow \left\{ \begin{matrix} \sin\alpha > 0 \\ \cos\alpha > 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 7: Vận dụng

    Từ một đỉnh tháp chiều cao CD = 80\ m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 72^{0}12' và 34^{0}26' so với phương nằm ngang. Ba điểm A,B,D thẳng hàng. Tính khoảng cách AB (chính xác đến hàng đơn vị)?

    Ta có: Trong tam giác vuông CDA: tan72^{0}12' = \frac{CD}{AD} \Rightarrow AD = \frac{CD}{tan72^{0}12'} = \frac{80}{tan72^{0}12'} \simeq 25,7.

    Trong tam giác vuông CDB: tan34^{0}26' = \frac{CD}{BD} \Rightarrow BD = \frac{CD}{tan34^{0}26'} = \frac{80}{tan34^{0}26'} \simeq 116,7.

    Suy ra: khoảng cách AB = 116,7 - 25,7 = 91\ m.

  • Câu 8: Nhận biết

    Chọn công thức đúng trong các đáp án sau:

    Ta có: S = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B = \frac{1}{2}ab\sin C.

  • Câu 9: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha > 0 \\ \tan\alpha < 0 \\ \cot\alpha < 0 \\ \end{matrix} ight..

  • Câu 10: Nhận biết

    Cho tam giác ABC có AB = 12,AC = 13,BC = 5. Diện tích S của tam giác ABC là:

    Ta có: BA^{2} + BC^{2} = AC^{2} nên tam giác ABC vuông tại B.

    Diện tích tam giác là: S = \frac{1}{2}BA \cdot BC = 30.

  • Câu 11: Vận dụng cao

    Tam giác ABC là tam giác gì khi có các góc thỏa mãn biểu thức

    \sin2\widehat{A}.\cos2\widehat{A} +\sin2\widehat{B}.\cos2\widehat{B} + \sin2\widehat{C}.\cos2\widehat{C} =0?

    Ta có:

    \sin2\widehat{A}.\cos2\widehat{A} +\sin2\widehat{B}.\cos2\widehat{B} + \sin2\widehat{C}.\cos2\widehat{C} =0

    \Leftrightarrow2\sin2\widehat{A}.\cos2\widehat{A} + 2\sin2\widehat{B}.\cos2\widehat{B} +\sin2\widehat{C}.\cos2\widehat{C} = 0

    \Leftrightarrow \sin4\widehat{A} +\sin4\widehat{B} + 2\sin2\widehat{C}.\cos2\widehat{C} = 0

    \Leftrightarrow 2\sin2\left( \widehat{A}+ \widehat{B} ight).\cos2\left( \widehat{A} - \widehat{B} ight) +2\sin2\widehat{C}.\cos2\left( \widehat{A} + \widehat{B} ight) =0

    \Leftrightarrow -2\sin2\widehat{C}.\left\lbrack \cos2\left( \widehat{A} - \widehat{B}ight) - \cos2\left( \widehat{A} + \widehat{B} ight) ightbrack =0

    \Leftrightarrow -4\sin2\widehat{C}.\sin2A.\sin2B = 0

    \Leftrightarrow \left\lbrack\begin{matrix}\sin2\widehat{C} = 0 \\\sin2\widehat{A} = 0 \\\sin2\widehat{B} = 0 \\\end{matrix} ight.

    \Leftrightarrow \left\lbrack\begin{matrix}2\widehat{C} = \pi \\2\widehat{A} = \pi \\2\widehat{A} = \pi \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}\widehat{C} = \dfrac{\pi}{2} \\\widehat{A} = \dfrac{\pi}{2} \\\widehat{A} = \dfrac{\pi}{2} \\\end{matrix} ight.

    Vậy tam giác ABC là tam giác vuông.

  • Câu 12: Thông hiểu

    Tam giác ABC có \widehat{B}=60°,\widehat{C}=45° và AB=5. Tính độ dài cạnh AC.

     Áp dụng định lí sin: 

    \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow AC = \sin B.\frac{{AB}}{{\sin C}}= \sin 60^\circ .\frac{5}{{\sin 45^\circ }} = \frac{{5\sqrt 6 }}{2}.

  • Câu 13: Nhận biết

    Tam giác ABC có AB = 5,\ \ BC = 7,\ \ CA = 8. Số đo góc \widehat{A} bằng:

    Theo định lí hàm cosin, ta có \cos\widehat{A} = \frac{AB^{2} + AC^{2} - BC^{2}}{2AB.AC} = \frac{5^{2} + 8^{2} - 7^{2}}{2.5.8} = \frac{1}{2}.

    Do đó, \widehat{A} = 60{^\circ}.

  • Câu 14: Vận dụng

    Cho góc \alpha thỏa mãn \tan\alpha = 2. Tính P = \frac{3sin\alpha - 2cos\alpha}{5cos\alpha + 7sin\alpha}.

    Chia cả tử và mẫu của P cho \cos\alpha ta được P = \frac{3tan\alpha - 2}{5 + 7tan\alpha} = \frac{3.2 - 2}{5 + 7.2} = \frac{4}{19}

  • Câu 15: Nhận biết

    Trong các khẳng định sau, khẳng định nào là đúng?

     Ta có: \sin157^{\circ} =\sin (180^{\circ} -157^{\circ} )=\sin 23^{\circ}. Vì \sin \alpha =\sin (180^{\circ} -\alpha ).

  • Câu 16: Thông hiểu

    Giá trị biểu thức A = \sin {30^0}.\cos {60^0} + \sin {60^0}.\cos {30^0} là:

    Ta có:

    \begin{matrix} A = \sin {30^0}.\cos {60^0} + \sin {60^0}.\cos {30^0} \hfill \\ A = \dfrac{1}{2}.\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} \hfill \\ A = \dfrac{1}{4} + \dfrac{3}{4} = 1 \hfill \\ \end{matrix}

  • Câu 17: Nhận biết

    Cho tam giác ABC có AB =4cm;AC = 12cm và góc \widehat{BAC} = 120^{\circ}. Tính diện tích tam giác ABC.

    S = \frac{1}{2}AB \cdot AC \cdot \sin\widehat{BAC}

    = \frac{1}{2} \cdot 4 \cdot 12 \cdot \sin 120^{\circ}

    = 12\sqrt{3}\left( {cm}^{2}ight)

  • Câu 18: Nhận biết

    Cho tam giác ABC có a = 8,b = 10, góc C bằng 60^{0} . Độ dài cạnh c là ?

    Ta có: c^{2} = a^{2} + b^{2} - 2a.b.cosC = 8^{2} + 10^{2} - 2.8.10.cos60^{0} = 84 \Rightarrow c = 2\sqrt{21}.

  • Câu 19: Thông hiểu

    Cho góc \alpha thỏa mãn \sin\alpha = \frac{12}{13} và \frac{\pi}{2} < \alpha < \pi. Tính \cos\alpha.

    Ta có: \left\{ \begin{matrix} \cos\alpha = \pm \sqrt{1 - sin^{2}\alpha} = \pm \frac{5}{13} \\ \frac{\pi}{2} < \alpha < \pi \\ \end{matrix} ight. \overset{}{ightarrow}\cos\alpha = - \frac{5}{13}.

  • Câu 20: Vận dụng cao

    Với mọi góc \alpha, giá trị của biểu thức

    \cos\alpha + \cos\left( \alpha + \frac{\pi}{5} ight) + \cos\left( \alpha + \frac{2\pi}{5} ight) + ... + \cos\left( \alpha + \frac{9\pi}{5} ight)

    Ta có:

    \cos\alpha = - \cos\left( \alpha + \frac{5\pi}{5} ight)

    \cos\left( \alpha + \frac{\pi}{5} ight) = - \cos\left( \alpha + \frac{6\pi}{5} ight)

    \cos\left( \alpha + \frac{2\pi}{5} ight) = - \cos\left( \alpha + \frac{7\pi}{5} ight)

    \cos\left( \alpha + \frac{3\pi}{5} ight) = - \cos\left( \alpha + \frac{8\pi}{5} ight)

    \cos\left( \alpha + \frac{4\pi}{5} ight) = - \cos\left( \alpha + \frac{9\pi}{5} ight)

    Do đó:

    \cos\alpha + \cos\left( \alpha + \frac{\pi}{5} ight) + \cos\left( \alpha + \frac{2\pi}{5} ight) + ... + \cos\left( \alpha + \frac{9\pi}{5} ight) = 0

  • Câu 21: Nhận biết

    Tam giác ABC có \hat B = {60^0},\hat C = {45^0};AC = 5. Độ dài cạnh AB là:

    Áp dụng định lí sin trong tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin B}} = \dfrac{{AB}}{{\sin C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin C}}{{\sin B}} = \dfrac{{5.\sin {{45}^0}}}{{\sin {{60}^0}}} = \dfrac{{5\sqrt 6 }}{3} \hfill \\ \end{matrix}

  • Câu 22: Thông hiểu

    Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230m. Góc giữa hai hàng rào MN và MP là 110^{\circ} (như hình vẽ).

    Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

    Áp dụng định li côsin ta

    NP^{2} = MN^{2} + MP^{2} - 2MN \cdot MP \cdot \cos M

    = 150^{2} + 230^{2} - 2 \cdot 150 \cdot 230 \cdot cos110^{\circ} \approx 98999,39.

    Suy ra NP \approx \sqrt{98999,39} \approx 314,6(m).

    Vậy chiều dài hàng rào NP là khoảng 314,6m.

  • Câu 23: Thông hiểu

    Tam giác ABC có AB=\sqrt{2},AC=\sqrt{3} và \widehat{C}=45°. Tính độ dài cạnh BC.

     Áp dụng định lý côsin: A{B^2} = C{A^2} + C{B^2} - 2CA.CB.\cos 45^\circ\Leftrightarrow 2 = 3 + C{B^2} - 2\sqrt 3 .CB.\frac{{\sqrt 2 }}{2}\Leftrightarrow C{B^2} - \sqrt 6 CB + 1 = 0\Rightarrow BC=\frac{{\sqrt 6 + \sqrt 2 }}{2}.

     

  • Câu 24: Thông hiểu

    Nếu tam giác ABC có BC^{2} < AB^{2} + AC^{2} thì:

    Nếu tam giác ABC có BC^{2} < AB^{2} + AC^{2} thì \widehat{A} là góc nhọn

  • Câu 25: Thông hiểu

    Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?

    Hình ảnh minh họa

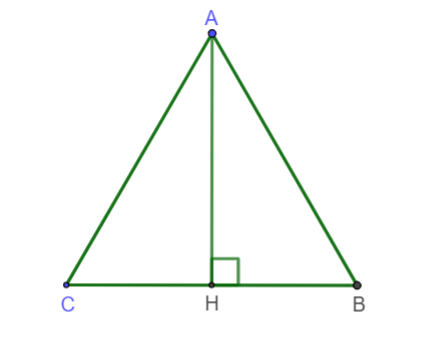
    Chọn khẳng định đúng

    Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường phân giác

    => \widehat {BAH} = \frac{1}{2}\widehat {BAC}=30^0;\widehat {ABC} = {60^0};\widehat {AHC} = {90^0}

    Do đó: \sin \widehat {BAH} = \frac{1}{2};\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}

    Ta có: \widehat {ABC} = {60^0} \Rightarrow \sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}

  • Câu 26: Thông hiểu

    Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230m. Góc giữa hai hàng rào MN và MP là 110^{\circ} (như hình vẽ)

    Diện tích mảnh đất mà gia đình bà Sáu sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?

    Diện tích mảnh đất của gia đình bà Sáu (tam giác MNP) là:

    S = \frac{1}{2}MN \cdot MP \cdot \sin M

    = \frac{1}{2} \cdot 150 \cdot 230 \cdot \sin110^{\circ} \approx 16209,7\left( {m}^{2}ight).

  • Câu 27: Nhận biết

    Tam giác ABC có AB = 2,\ \ AC = 1 và \widehat{A} = 60{^\circ}. Tính độ dài cạnh BC.

    Theo định lí hàm cosin, ta có BC^{2} = AB^{2} + AC^{2} - 2AB.AC.cos\widehat{A} = 2^{2} + 1^{2} - 2.2.1.cos60{^\circ} = 3 \Rightarrow BC = \sqrt{3}.

  • Câu 28: Nhận biết

    Cho tam giác ABC có a=2,\hat A=60^{\circ} ,\hat B=45^{\circ}. Hỏi độ dài cạnh b bằng bao nhiêu?

     Áp dụng định lí sin:

    \frac{a}{{\sin A}} = \frac{b}{{\sin B}} \Leftrightarrow b = \sin B.\frac{a}{{\sin A}}= \sin 45^\circ .\frac{2}{{\sin 60^\circ }} = \frac{{2\sqrt 6 }}{3}.

  • Câu 29: Nhận biết

    Cho tam giác ABC thỏa mãn: 2cosA = 1. Khi đó:

    Ta có: 2cosA = 1 \Leftrightarrow \cos A = \frac{1}{2} \Rightarrow \widehat{A} = 60^{0}.

  • Câu 30: Nhận biết

    Cho tam giác ABC có AB=1;AC=\sqrt2;\hat A=45^{\circ}. Tính độ dài cạnh BC.

     Áp dụng định lí côsin:

    BC^2=AB^2+AC^2-2.AB.AC.\cos A=1+2-2.1.\sqrt2.\cos45^{\circ} =1.

    Suy ra BC=1.

  • Câu 31: Thông hiểu

    Tam giác ABC có BC=5\sqrt{5},AC=5\sqrt{2},AB=5 . Số đo góc A là:

    Áp dụng định lí cosin trong tam giác ta có:

    \begin{matrix} B{C^2} = A{B^2} + A{C^2} - 2AB.AC\cos \widehat A \hfill \\ \Leftrightarrow \cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = - \dfrac{{\sqrt 2 }}{2} \hfill \\ \Rightarrow \widehat A = {135^0} \hfill \\ \end{matrix}

  • Câu 32: Thông hiểu

    Tam giác ABC có AB = \sqrt{2},\ \ AC = \sqrt{3} và \widehat{C} = 45{^\circ}. Tính độ dài cạnh BC.

    Theo định lí hàm cosin, ta có

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{C}

    \Rightarrow \left( \sqrt{2} ight)^{2} = \left( \sqrt{3} ight)^{2} + BC^{2} - 2.\sqrt{3}.BC.cos45{^\circ}

    \Rightarrow BC = \frac{\sqrt{6} + \sqrt{2}}{2}.

  • Câu 33: Vận dụng

    Vào lúc 9 giờ sáng, hai vận động viên A và B xuất phát từ cùng một vị trí O. Vận động viên A chạy với vận tốc 13 km/h theo một góc so với hướng Bắc là 15°, vận động viên B chạy với vận tốc 12 km/h theo một góc so với hướng Bắc là 135° (hình vẽ).

    Tính thời điểm hai vận động viên cách nhau 10km

    Tại thời điểm nào thì vận động viên A cách vận động viên B một khoảng 10 km (làm tròn kết quả đến phút)?

    Gọi khoảng thời gian kể từ khi bắt đầu chạy từ điểm O đến khi hai vận động viên cách nhau 10 km là x giờ

    Điều kiện: x > 0

    Khi đó đoạn đường mà vận động viên A chạy được là 13x (km)

    Đoạn đường mà vận động viên B chạy được là 12x (km)

    Ta có: \widehat {AOB} = {135^0} - {15^0} = {120^0}

    Áp dụng định lí cosin cho tam giác ABC ta có:

    \begin{matrix} A{B^2} = B{C^2} + A{C^2} - 2BC.AC.\cos \widehat {AOB} \hfill \\ \Leftrightarrow {10^2} = {\left( {13x} ight)^2} + {\left( {12x} ight)^2} - 2.13x.12x.\cos {120^0} \hfill \\ \Leftrightarrow {10^2} = 169{x^2} + 144{x^2} + 156{x^2} \hfill \\ \Leftrightarrow {x^2} = \dfrac{{100}}{{469}} \hfill \\ \Rightarrow x \approx 0,46 \hfill \\ \end{matrix}

    0,46 giờ ≈ 28 phút

    Do đó thời điểm mà hai vận động viên cách nhau 10 km là khoảng: 9 giờ 28 phút.

    Vậy vào khoảng 9 giờ 28 phút thì hai vận động viên sẽ cách nhau 10 km.

  • Câu 34: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha < 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 35: Nhận biết

    Trong các khẳng định sau, khẳng định nào là đúng?

     Ta có: \cos 121^{\circ} =\cos -121^{\circ} vì \cos \alpha =\cos -\alpha.

  • Câu 36: Vận dụng cao

    Cho tam giác ABC có AB = c;BC = a;AC = b và các góc của tam giác thỏa mãn biểu thức:

    \left\{ \begin{matrix}\sin\widehat{B}.\sin\widehat{C} = \dfrac{3}{4} \\a^{2} = \dfrac{a^{3} - b^{3} - c^{3}}{a - b - c} \\\end{matrix} ight.. Khi đó tam giác ABC là tam giác gì?

    Ta có:

    a^{2} = \frac{a^{3} - b^{3} - c^{3}}{a - b - c}

    \Leftrightarrow a^{2}(a - b - c) = a^{3} - b^{3} - c^{3}

    \Leftrightarrow a^{2}(a + b) = (b + c)\left( b^{2} - bc + c^{2} ight)

    \Leftrightarrow a^{2} = b^{2} - bc + c^{2}

    \Leftrightarrow b^{2} + c^{2} - a^{2} = bc

    \Leftrightarrow \frac{b^{2} + c^{2} - a^{2}}{2bc} = \frac{1}{2}

    \Leftrightarrow \cos\widehat{A} = \frac{1}{2}

    \Leftrightarrow \widehat{A} = \frac{\pi}{3}(*)

    Ta lại có:

    \sin\widehat{B}.sin\widehat{C} = \frac{3}{4}

    \Leftrightarrow \cos\left( \widehat{B} - \widehat{C} ight) - \cos\left( \widehat{B} + \widehat{C} ight) = \frac{3}{2}

    \Leftrightarrow \cos\left( \widehat{B} - \widehat{C} ight) + \cos\widehat{A} = \frac{3}{2}

    \Leftrightarrow \cos\left( \widehat{B} - \widehat{C} ight) = 1

    \Leftrightarrow \widehat{B} - \widehat{C} = 0 \Leftrightarrow \widehat{B} = \widehat{C}

    Vậy tam giác ABC là tam giác đều.

  • Câu 37: Thông hiểu

    Cho hình thoi ABCD cạnh bằng 1\ \ cm và có \widehat{BAD} = 60{^\circ}. Tính độ dài cạnh AC.

    Do ABCD là hình thoi, có \widehat{BAD} = 60{^\circ} \Rightarrow \widehat{ABC} = 120{^\circ}.

    Theo định lí hàm cosin, ta có

    AC^{2} = AB^{2} + BC^{2} - 2.AB.BC.cos\widehat{ABC}

    = 1^{2} + 1^{2} - 2.1.1.cos120{^\circ} = 3 \Rightarrow AC = \sqrt{3}

  • Câu 38: Nhận biết

    Cho 2\pi < \alpha < \frac{5\pi}{2}. Khẳng định nào sau đây đúng?

    Ta có 2\pi < \alpha < \frac{5\pi}{2}\overset{}{ightarrow}điểm cuối cung \alpha - \pi thuộc góc phần tư thứ I\overset{}{ightarrow}\left\{ \begin{matrix} \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight.\ .

  • Câu 39: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \cos\alpha = \sqrt{1 - sin^{2}\alpha}.

    Ta có \cos\alpha = \sqrt{1 - sin^{2}\alpha} \Leftrightarrow \cos\alpha = \sqrt{cos^{2}\alpha} \Leftrightarrow \cos\alpha = \left| \cos\alpha ight| \Leftrightarrow \cos\alpha.

    Đẳng thức \left| \cos\alpha ight| \Leftrightarrow \cos\alpha\overset{}{ightarrow}\cos\alpha \geq 0\overset{}{ightarrow}điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc IV.

  • Câu 40: Thông hiểu

    Cho \pi < \alpha < \frac{3\pi}{2}. Khẳng định nào sau đây đúng?

    Ta có : \pi < \alpha < \frac{3\pi}{2} ightarrow 0 < \frac{3\pi}{2} - \alpha < \frac{\pi}{2}\overset{}{ightarrow} \left\{ \begin{matrix} \sin\left( \frac{3\pi}{2} - \alpha ight) > 0 \\ \cos\left( \frac{3\pi}{2} - \alpha ight) > 0 \\ \end{matrix} ight. \overset{}{ightarrow}\tan\left( \frac{3\pi}{2} - \alpha ight) > 0.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác Sách CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 45 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác Sách CTST
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập