Cho tam giác đều ![]() cạnh
cạnh ![]() . Tính độ dài
. Tính độ dài ![]() .
.
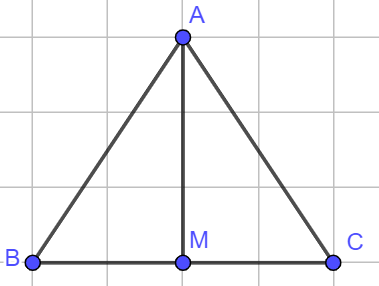
Gọi là trung điểm
. Suy ra
.
Áp dụng định lí Pytago trong tam giác vuông . Suy ra
.
Cho tam giác đều ![]() cạnh
cạnh ![]() . Tính độ dài
. Tính độ dài ![]() .
.

Gọi là trung điểm
. Suy ra
.
Áp dụng định lí Pytago trong tam giác vuông . Suy ra
.
Cho ba điểm phân biệt ![]() Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
Đáp án chỉ đúng khi ba điểm
thẳng hàng và
nằm giữa
.
Đáp án đúng theo quy tắc ba điểm. Chọn đáp án này.
Tam giác ABC có ![]() . Số đo góc A là:
. Số đo góc A là:
Áp dụng định lí cosin trong tam giác ta có:
Trong mặt phẳng tọa độ ![]() , gọi
, gọi ![]() là trực tâm tam tam giác
là trực tâm tam tam giác ![]() có tọa độ các đỉnh
có tọa độ các đỉnh ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có: là trực tâm tam giác ABC nên
Ta có hệ phương trình
Vậy biểu thức
Cho 4 điểm ![]() phân biệt. Khi đó
phân biệt. Khi đó ![]() bằng
bằng
.
Trong hệ tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() , trọng tâm
, trọng tâm ![]() và trung điểm cạnh
và trung điểm cạnh ![]() là
là ![]() Tổng hoành độ của điểm
Tổng hoành độ của điểm ![]() và
và ![]() là
là
Vì là trung điểm
nên
Vì là trọng tâm tam giác
nên
Suy ra
Cho hình bình hành ABCD. Với mọi điểm M, ta có khẳng định nào sau đây:
Gọi O là giao điểm của AC và BD
=> OA OC, OB = OD
Ta có:
Tính giá trị biểu thức ![]() .
.
Ta có:
Khi đó:
Cho tam giác ABC, có thể xác định được bao nhiêu vectơ khác ![]() có điểm đầu và điểm cuối là các đỉnh A, B, C?
có điểm đầu và điểm cuối là các đỉnh A, B, C?
Ta có các vectơ khác có điểm đầu và điểm cuối là các đỉnh tam giác ABC là:
Cho đoạn thẳng ![]() và
và ![]() là một điểm trên đoạn
là một điểm trên đoạn ![]() sao cho
sao cho ![]() . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai?
Hình vẽ minh họa
Ta thấy và
cùng hướng nên
là sai.
Cho hình thoi ![]() có
có ![]() . Tính
. Tính ![]() .
.
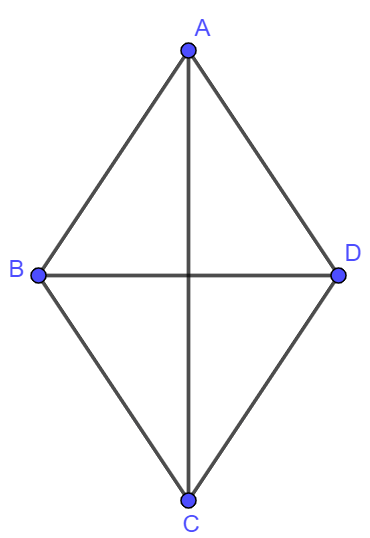
Vì nên
.
Cho góc ![]() . Gọi
. Gọi ![]() và
và ![]() là hai điểm di động lần lượt trên
là hai điểm di động lần lượt trên ![]() và
và ![]() sao cho
sao cho ![]() . Độ dài lớn nhất của đoạn
. Độ dài lớn nhất của đoạn ![]() bằng:
bằng:
Theo định lí hàm sin, ta có:
Do đó, độ dài lớn nhất khi và chỉ khi
.
Khi đó .
Cho ba điểm ![]() phân biệt. Khi đó:
phân biệt. Khi đó:
Chọn: Điều kiện cần và đủ để thẳng hàng là
cùng phương với
Cho ba điểm phân biệt A, B, C. Khẳng định nào sau đây đúng?
Ta có:
=> Khẳng định sai
=> Khẳng định sai
=> Khẳng định đúng
=> Khẳng định sa
Cho hình vuông ![]() cạnh bằng
cạnh bằng ![]() . Tính độ dài véctơ
. Tính độ dài véctơ ![]() .
.
Hình vẽ minh họa:
Tính giá trị ![]() biết rằng
biết rằng ![]() ?
?
Ta có:
Giá trị ![]() là:
là:
Ta có: .
Nếu tam giác ![]() có
có ![]() thì:
thì:
Nếu tam giác ABC có thì
là góc nhọn
Điểm cuối của ![]() thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
Điểm cuối của thuộc góc phần tư thứ nhất
.
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Tính
. Tính ![]()
Ta có
Trong mặt phẳng tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() và
và ![]() . Tính số đo góc
. Tính số đo góc ![]() của tam giác đã cho.
của tam giác đã cho.
Ta có: và
.
.
Cho hai điểm ![]() phân biệt và cố định, với
phân biệt và cố định, với ![]() là trung điểm của
là trung điểm của ![]() Tập hợp các điểm
Tập hợp các điểm ![]() thỏa mãn đẳng thức
thỏa mãn đẳng thức ![]() là
là
Chọn điểm thuộc đoạn
sao cho
Chọn điểm thuộc đoạn
sao cho
Ta có
Vì là hai điểm cố định nên từ đẳng thức
suy ra tập hợp các điểm
là trung trực của đoạn thẳng
Gọi
là trung điểm của
suy ra
cũng là trung điểm của
Vậy tập hợp các điểm thỏa mãn
là đường trung trực của đoạn thẳng
Cho lục giác đều ![]() có tâm
có tâm ![]() Đẳng thức nào sau đây sai?
Đẳng thức nào sau đây sai?
Đẳng thức sai là
Cho tam giác ![]() có
có![]() và
và ![]() . Biết rằng:
. Biết rằng:

Chọn khẳng định đúng?
Ta có:
Mà
Vậy tam giác ABC là tam giác vuông tại A.
Cho tam giác ![]() có
có ![]() . Hỏi độ dài cạnh b bằng bao nhiêu?
. Hỏi độ dài cạnh b bằng bao nhiêu?
Áp dụng định lí sin:
.
Cho hình vuông ![]() , tính
, tính ![]() .
.
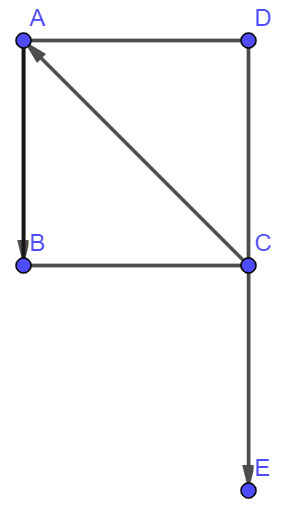
Vẽ .
Ta có: .
Cho tam giác ABC có I là trung điểm của AB. Điểm M thỏa mãn ![]() . Chọn mệnh đề đúng.
. Chọn mệnh đề đúng.
.
Khẳng định nào sau đây đúng?
Theo định nghĩa, hai véctơ bằng nhau phải thỏa mãn hai điều kiện:
+) Cùng hướng
+) Cùng độ dài.
Chọn đáp án: Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
Cho ![]() có
có ![]() Diện tích của tam giác là:
Diện tích của tam giác là:
Ta có:
Cho tam giác ![]() , kẻ đường cao
, kẻ đường cao ![]() và
và ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() ,
, ![]() là điểm thỏa mãn
là điểm thỏa mãn ![]() và
và ![]() . Khi đó độ dài vectơ
. Khi đó độ dài vectơ ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
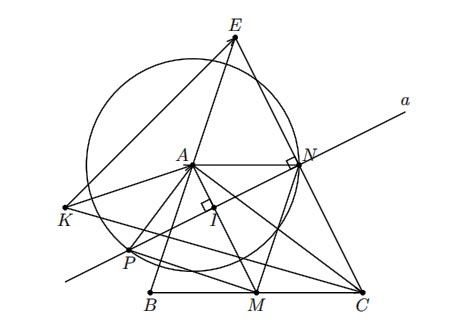
Gọi E là điểm đối xứng của B qua A, ta có:
Nên K thuộc đường thẳng a là trung trực của đoạn thẳng CE, mặt khác
Suy ra K là giao điểm của a và đường tròn tâm A bán kính .
Điểm K cần tìm là N hoặc P
Ta có: .
Cho hai lực ![]() và
và ![]() có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực
có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực ![]() và
và ![]() lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là:
lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là:
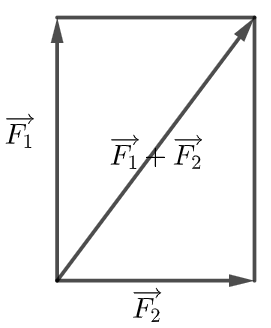
Ta có: .
Cho tam giác đều ![]() với đường cao
với đường cao ![]() . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
Chọn vì
là trung điểm
và
cùng hướng.
Cho tam giác ![]() . Tìm công thức sai:
. Tìm công thức sai:
Ta có:
Cho ![]() có
có ![]() Độ dài bán kính đường tròn ngoại tiếp
Độ dài bán kính đường tròn ngoại tiếp ![]() của tam giác trên là:
của tam giác trên là:
Ta có:
.
Cho ![]() . Xác định dấu của biểu thức
. Xác định dấu của biểu thức ![]()
Ta có:
và
.
Cho tam giác ![]() có
có ![]() là một đường trung tuyến. Biểu diễn vectơ
là một đường trung tuyến. Biểu diễn vectơ ![]() theo hai vectơ
theo hai vectơ ![]() và
và ![]() .
.
Vì là trung điểm
nên
.
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() .
.
Điểm là trung điểm của đoạn
khi và chỉ khi
và ngược hướng.
Vậy .
Biết ![]() và
và ![]() . Câu nào sau đây đúng?
. Câu nào sau đây đúng?
Ta có: .
Suy ra và
ngược hướng.
Cho hình bình hành ![]() Gọi
Gọi ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
Vì là trọng tâm của tam giác
nên
Do đó
Cho góc ![]() thoả mãn
thoả mãn ![]() và
và ![]() . Giá trị của
. Giá trị của ![]() là:
là:
Ta có:
.
Do đó .
Vì nên
.
