Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng?
Áp dụng quy tắc hình bình hành tại điểm B ta có:
Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng?
Áp dụng quy tắc hình bình hành tại điểm B ta có:
Cho hình chữ nhật ABCD có AB = 8, AD = 5. Tính ![]() .
.
Do ABCD là hình chữ nhật =>
Xét tam giác ABD vuông tại A ta có:
Ta lại có:
Cho tam giác ABC và điểm M thỏa mãn ![]() Xác định vị trí điểm M.
Xác định vị trí điểm M.
Giả sử G là trọng tâm tam giác ABC, khi đó ta có:
=> M là trọng tâm của tam giác ABC.
Cho ba điểm ![]() phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là
phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là
Ta có tính chất: Điều kiện cần và đủ để ba điểm phân biệt thẳng hàng là
.
Gọi ![]() là các trung tuyến của tam giác
là các trung tuyến của tam giác ![]() . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
Ta có
Suy ra
Do đó .
Trên đường thẳng MN lấy điểm P sao cho ![]() . Điểm P được xác định đúng trong hình vẽ nào sau đây:
. Điểm P được xác định đúng trong hình vẽ nào sau đây:
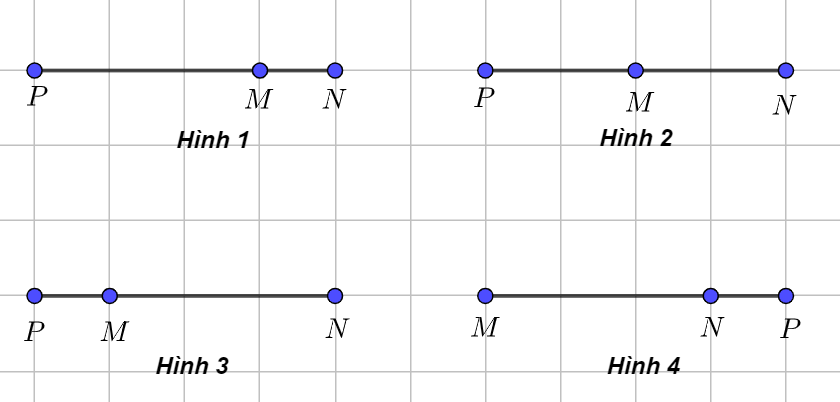
Vì nên
nằm giữa
và
, đồng thời
.
Cho mặt phẳng Oxy, cho ∆ABC có G là trọng tâm. Biết B(4; 1), C(1; –2) và G(2; 1). Tọa độ điểm A là:
Theo bài ra:
G là trọng tâm tam giác ABC nên ta có:
Cho hình vuông ![]() cạnh
cạnh ![]() Tính
Tính ![]()
Ta có
Trong hệ tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() và trọng tâm
và trọng tâm ![]() . Tìm tọa độ đỉnh
. Tìm tọa độ đỉnh ![]() ?
?
Gọi
Vì là trọng tâm tam giác
nên
Cho hình bình hành ABCD, với giao điểm hai đường chéo I. Khi đó:
Ta có: (2 vectơ đối nhau).
Cho tam giác đều ![]() có cạnh bằng
có cạnh bằng ![]() Tính tích vô hướng
Tính tích vô hướng ![]()
.
Trong mặt phẳng tọa độ ![]() , tọa độ vecto
, tọa độ vecto ![]() là:
là:
Ta có: .
Cho tam giác ![]() có
có ![]() thỏa mãn điều kiện
thỏa mãn điều kiện ![]() . Xác định vị trí điểm
. Xác định vị trí điểm ![]()
Gọi là trọng tâm tam giác
.
Ta có .
Cho hình bình hành ABCD tâm O. Khi đó ![]() bằng:
bằng:
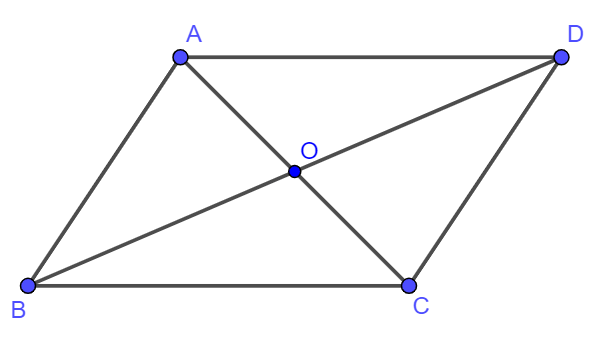
Ta có:
Cho tam giác ABC đều cạnh 2a. Đẳng thức nào sau đây là đúng?
Theo bài ra ta có:
Tam giác ABC đều cạnh 2a => AB = BC = AC = 2a
=>
Cho ba vectơ ![]() Giá trị của
Giá trị của ![]() để
để ![]() là
là
Ta có
Theo đề bài:
Cho tam giác ![]() đều cạnh
đều cạnh ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]() ,
, ![]() là một điểm thay đổi trên
là một điểm thay đổi trên ![]() . Gọi
. Gọi ![]() lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức ![]() . Tính tổng
. Tính tổng ![]() .
.
Hình vẽ minh họa
Dựng hình bình hành DBCA. Ta có:
Gọi E là giao điểm khác C của DC với (O). Áp dụng bất đẳng thức tam giác ta có:
Dấu bằng xảy ra khi và chỉ khi M trùng E và M trùng C.
Vậy
Cho ![]() và
và ![]() là các vectơ khác
là các vectơ khác ![]() với
với ![]() là vectơ đối của
là vectơ đối của ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Ta có . Do đó,
và
cùng phương, cùng độ dài và ngược hướng nhau.
Chọn đáp án sai là: Hai vectơ chung điểm đầu.
Cho hình bình hành ![]() Tính
Tính ![]() theo
theo ![]() và
và ![]()
Vì là hình bình hành nên
Ta có
Gọi ![]() là giao điểm của hai đường chéo hình chữ nhật
là giao điểm của hai đường chéo hình chữ nhật ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Mệnh đề đúng là Do độ dài hai đường chéo hình chữ nhật bằng nhau.
Cho tam giác ABC và điểm M thỏa mãn ![]() . Xác định vị trí điểm M.
. Xác định vị trí điểm M.
Điểm là trọng tâm tam giác
khi và chỉ khi
.
Cho tam giác ![]() . Lấy các điểm
. Lấy các điểm ![]() sao cho
sao cho ![]() và
và ![]() . Xác định
. Xác định ![]() để ba điểm
để ba điểm ![]() thẳng hàng.
thẳng hàng.
Ta có:
Để ba điểm thẳng hàng thì
hay
Cho hình vuông ![]() , tính
, tính ![]() .
.
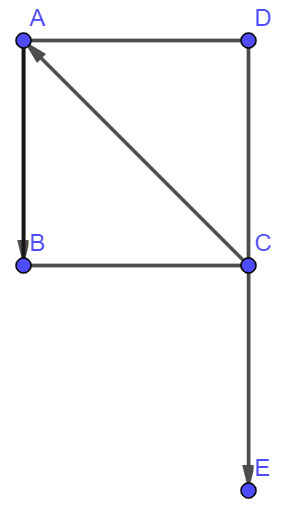
Vẽ .
Ta có: .
Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() của tam giác đều
của tam giác đều ![]() . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
Ta có là đường trung bình của tam giác
.
Do đó
Cho đoạn thẳng ![]() và
và ![]() là một điểm trên đoạn
là một điểm trên đoạn ![]() sao cho
sao cho ![]() . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai?
Hình vẽ minh họa
Ta thấy và
cùng hướng nên
là sai.
Cho hình thoi ![]() có
có ![]() . Tính
. Tính ![]() .
.
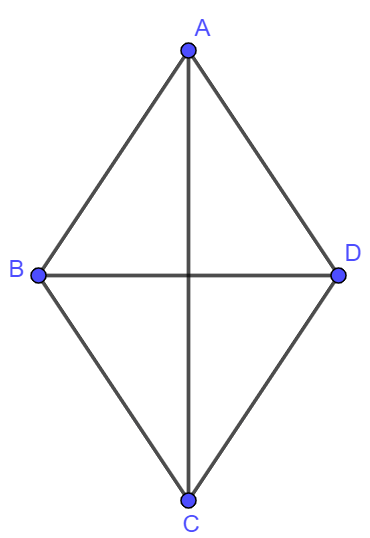
Vì nên
.
Cho tam giác ![]() Có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là các đỉnh
Có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là các đỉnh ![]()
Đó là các vectơ:
Cho ![]() và một điểm
và một điểm ![]() Có bao nhiêu điểm
Có bao nhiêu điểm ![]() thỏa mãn
thỏa mãn ![]()
Ta có . Suy ra tập hợp các điểm
thỏa mãn yêu cầu bài toán là đường tròn tâm
bán kính
.
Cho tam giác ![]() có
có ![]() là một đường trung tuyến. Biểu diễn vectơ
là một đường trung tuyến. Biểu diễn vectơ ![]() theo hai vectơ
theo hai vectơ ![]() và
và ![]() .
.
Vì là trung điểm
nên
.
Tứ giác MNPQ là hình bình hành nếu:
Hình vẽ minh họa
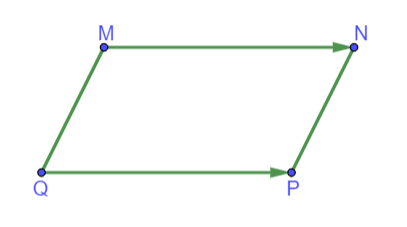
Ta có MNPQ là hình bình hành nếu
Cho ngũ giác ![]() . Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của ngũ giác đó?
. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của ngũ giác đó?
,
,
,
,
.
Trong hệ tọa độ ![]() cho ba điểm
cho ba điểm ![]() và
và ![]() Tìm điểm
Tìm điểm ![]() thuộc trục hoành sao cho biểu thức
thuộc trục hoành sao cho biểu thức ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Ta có
Chọn điểm sao cho
Gọi , từ
ta có
Khi đó
Để nhỏ nhất
nhỏ nhất. Mà
thuộc trục hoành nên
nhỏ nhất khi
là hình chiếu vuông góc của
lên trục hoành
Cho tam giác ![]() điểm
điểm ![]() thuộc cạnh
thuộc cạnh ![]() sao cho
sao cho ![]() và
và ![]() là trung điểm của
là trung điểm của ![]() Tính
Tính ![]() theo
theo ![]() và
và ![]()
Vì là trung điểm
nên
Suy ra
Trong mặt phẳng ![]() cho
cho ![]() . Tính
. Tính ![]() ?
?
Ta có ,
suy ra
.
Cho ![]() và tọa độ hai điểm
và tọa độ hai điểm ![]() . Biết
. Biết ![]() , tọa độ vecto
, tọa độ vecto ![]() là:
là:
Tọa độ vecto .
Cho đường tròn ![]() và hai tiếp tuyến song song với nhau tiếp xúc với
và hai tiếp tuyến song song với nhau tiếp xúc với ![]() tại hai điểm
tại hai điểm ![]() và
và ![]() Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
Do hai tiếp tuyến song song và là hai tiếp điểm nên
là đường kính.
Do đó là trung điểm của
.
Suy ra .
Trong mặt phẳng tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() và
và ![]() . Tính số đo góc
. Tính số đo góc ![]() của tam giác đã cho.
của tam giác đã cho.
Ta có: và
.
.
Cho ![]() ,
,![]() . Tính góc của
. Tính góc của ![]() .
.
Ta có .
Cho ![]() . Điểm
. Điểm ![]() trên trục
trên trục ![]() sao cho ba điểm
sao cho ba điểm ![]() thẳng hàng thì tọa độ điểm
thẳng hàng thì tọa độ điểm ![]() là:
là:
Ta có: trên trục
.
Ba điểm thẳng hàng khi
cùng phương với
.
Ta có . Do đó,
cùng phương với
. Vậy
.Đáp án là
Trong mặt phẳng tọa độ ![]() , khoảng cách giữa hai điểm
, khoảng cách giữa hai điểm ![]() và
và ![]() bằng:
bằng:
Khoảng cách giữa hai điểm M, N là
