Trong không gian với hệ tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng ![]()
![]() ?
?
Gọi lần lượt là vectơ chỉ phương của d1 và d2 ta chọn
Giả sử M1 ∈ d1 và M2 ∈ d2, ta chọn suy ra
Khi đó và
. Do đó (d1) và (d2) chéo nhau.
Trong không gian với hệ tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng ![]()
![]() ?
?
Gọi lần lượt là vectơ chỉ phương của d1 và d2 ta chọn
Giả sử M1 ∈ d1 và M2 ∈ d2, ta chọn suy ra
Khi đó và
. Do đó (d1) và (d2) chéo nhau.
Trong không gian với hệ toạ độ ![]() , cho phương trình
, cho phương trình![]() . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng ![]() , biết
, biết ![]() song song với mặt phẳng
song song với mặt phẳng ![]() và cắt mặt cầu theo thiết diện là một đường tròn có chu vi
và cắt mặt cầu theo thiết diện là một đường tròn có chu vi ![]() ?
?
Vì nên phương trình mặt phẳng (α) có dạng
Mặt cầu (S) có tâm và bán kính
.
Đường tròn lớn có chu vi là nên bán kính của
là
Khoảng cách từ tâm I đến mặt phẳng P bằng 3
Từ đó ta có:
Vì nên phương trình mặt phẳng (α) là
Trong không gian với hệ tọa độ ![]() , cho các điểm
, cho các điểm ![]() . Tìm tọa độ điểm H sao cho tứ giác
. Tìm tọa độ điểm H sao cho tứ giác ![]() lập thành hình thang cân với hai đáy
lập thành hình thang cân với hai đáy ![]() .
.
Ta có là trung điểm AB.
Gọi (α) là mặt phẳng trung trực của AB
Gọi d là đường thẳng qua C và song song AB
Gọi I là hình chiếu của C lên (α).
Tọa độ I là nghiệm của hệ phương trình:
Do ABCH là hình thang cân nên H và C đối xứng nhau qua mp(α).
⇒ I là trung điểm CH
Trong không gian với hệ trục tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng  và
và ![]() . Vị trí tương đối của
. Vị trí tương đối của ![]() và
và ![]() là
là
Đường thẳng d có vectơ chỉ phương và đi qua điểm M(−1; 0; 1).
Đường thẳng d’ có vectơ chỉ phương .
Hai vectơ và
cùng phương và điểm M không thuộc đường thẳng d’.
Do đó hai đường thẳng d và d’ song song với nhau.
Trong không gian với hệ tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng ![]() . Tìm tọa độ giao điểm
. Tìm tọa độ giao điểm ![]() của đường thẳng
của đường thẳng ![]() và
và ![]() , biết đường thẳng d' có phương trình
, biết đường thẳng d' có phương trình 
Tọa độ giao điểm I của d và d’ thỏa mãn hệ phương trình:
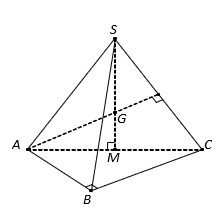
Cho hình chóp tứ giác đều ![]() có tất cả các cạnh bằng nhau. Gọi
có tất cả các cạnh bằng nhau. Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() và
và ![]() ,
, ![]() là góc tạo bởi đường thẳng
là góc tạo bởi đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() . Tính
. Tính ![]() ?
?
Hình vẽ minh họa
Không mất tính tổng quát, giả sử các cạnh của hình chóp bằng .
Chọn hệ trục tọa độ như hình vẽ.
Khi đó: và
là vectơ pháp tuyến của (SBD).
Do đó:
Vậy
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() có một vectơ pháp tuyến là:
có một vectơ pháp tuyến là:
Mặt phẳng có một vectơ pháp tuyến là:
.
Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() . Viết phương trình đường thẳng
. Viết phương trình đường thẳng ![]() ?
?
Vectơ chỉ phương của đường thẳng là
. Suy ra phương trình đường thẳng
là:
Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() và điểm
và điểm ![]() . Xét các điểm
. Xét các điểm ![]() sao cho đường thẳng
sao cho đường thẳng ![]() luôn tiếp xúc với
luôn tiếp xúc với ![]() . Điểm
. Điểm ![]() luôn thuộc một mặt phẳng cố định có phương trình là
luôn thuộc một mặt phẳng cố định có phương trình là
Tọa độ tâm mặt cầu là:
Gọi khi đó:
.
Theo đề bài ra ta có:
Mặt khác phương trình mặt cầu
Lấy (*) trừ (**) ta được: .
Trong không gian với hệ tọa độ ![]() , cho mặt cầu
, cho mặt cầu ![]() . Đường kính
. Đường kính ![]() bằng:
bằng:
Đường kính của mặt cầu bằng:
.
Trong không gian với hệ tọa độ ![]() , cho tam giác
, cho tam giác ![]() có
có ![]() . Độ dài đường cao của tam giác
. Độ dài đường cao của tam giác ![]() kẻ từ
kẻ từ ![]() là:
là:
Ta có:
Mà
Trong không gian với hệ tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() lần lượt có phương trình là
lần lượt có phương trình là ![]() và cho điểm
và cho điểm ![]() . Tìm phương trình mặt phẳng
. Tìm phương trình mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và đồng thời vuông góc với hai mặt phẳng
và đồng thời vuông góc với hai mặt phẳng ![]() ?
?
Ta có:
Do vuông góc với
nên
Chọn
Hơn nữa đi qua
nên có phương trình là:
Trong không gian ![]() cho hai mặt phẳng
cho hai mặt phẳng ![]() . Góc giữa hai mặt phẳng
. Góc giữa hai mặt phẳng ![]() bằng:
bằng:
Ta có: có 1 vectơ pháp tuyến là
có 1 vectơ pháp tuyến là
Khi đó:
Cho mặt cầu ![]() và một điểm A, biết
và một điểm A, biết ![]() . Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
Vì AB tiếp xúc với (S) tại B nên .
Suy ra
Trong không gian với hệ toạ độ ![]() , cho điểm
, cho điểm ![]() , Hai điểm
, Hai điểm ![]() thay đổi sao cho
thay đổi sao cho ![]() và
và ![]() . Mặt phẳng
. Mặt phẳng ![]() luôn tiếp xúc với một mặt cầu cố định đi qua
luôn tiếp xúc với một mặt cầu cố định đi qua ![]() có bán kính là
có bán kính là
Phương trình . Gọi
và
là tâm và bán kính mặt cầu cố định trong đề bài, phương trình mặt cầu là
.
Ta có khoảng cách từ đên
là
Vì
Nếu
Đẳng thức đúng với mọi nên
hay
, thay vào phương trình mặt cầu ta có R = 1.
Nếu
Đẳng thức đúng với mọi m ∈ (0; 1) nên hay
thay vào phương trình mặt cầu ta có
không thỏa mãn.
Vậy .
Trong không gian ![]() , cho ba điểm
, cho ba điểm ![]() . Phương trình nào dưới đây là phương trình mặt phẳng
. Phương trình nào dưới đây là phương trình mặt phẳng ![]() ?
?
Phương trình đoạn chắn của mặt phẳng là:
Trong không gian với hệ tọa độ ![]() , cho đường thẳng
, cho đường thẳng . Gọi
. Gọi ![]() là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng ![]() và tạo với mặt phẳng
và tạo với mặt phẳng ![]() một góc
một góc ![]() . Điểm nào sau đây thuộc mặt phẳng
. Điểm nào sau đây thuộc mặt phẳng ![]() ?
?
Ta viết phương trình đường thẳng
Mặt phẳng (P) chứa đường thẳng d nên có dạng:
⇒ có một vectơ pháp tuyến là
Mặt phẳng có một vectơ pháp tuyến là
Ta có:
Chọn
Trong không gian với hệ tọa độ ![]() ; cho điểm
; cho điểm ![]() . Gọi
. Gọi ![]() là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm ![]() trên ba trục tọa độ
trên ba trục tọa độ ![]() . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng ![]() ?
?
Có là hình chiếu của
lên các trục tọa độ nên mặt phẳng cần tìm là
Trong không gian ![]() , hãy tính
, hãy tính ![]() và
và ![]() lần lượt là khoảng cách từ điểm
lần lượt là khoảng cách từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]() và mặt phẳng
và mặt phẳng ![]() ?
?
Do mặt phẳng có phương trình y = 0 nên
Do mặt phẳng (P) có phương trình 3x − 4z + 5 = 0 nên
Trong không gian với hệ tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() và điểm
và điểm ![]() . Hình chiếu vuông góc của A trên (∆) là điểm nào dưới đây?
. Hình chiếu vuông góc của A trên (∆) là điểm nào dưới đây?
Đường thẳng (∆) đi qua M(−1; −4; 0), có vectơ chỉ phương
Phương trình tham số của đường thẳng
Gọi P là hình chiếu vuông góc của A trên (∆).
Khi đó
Ta có . Vì
nên
Phương trình tổng quát của mặt phẳng qua A(3,-1, 2), B(4, -2, -1), C(2, 0, 2) là:
Theo đề bài, ta có được các vecto sau:
Vì mặt phẳng đi qua 3 điểm nên VTPT của mp là tích có hướng của và
.
Chọn làm một vectơ pháp tuyến.
Phương trình mp có dạng
là mp qua A
Vậy phương trình .
Trong không gian với hệ tọa độ ![]() , cho điểm
, cho điểm ![]() và mặt phẳng
và mặt phẳng ![]() . Đường thẳng đi qua điểm
. Đường thẳng đi qua điểm ![]() và vuông góc với mặt phẳng
và vuông góc với mặt phẳng ![]() có phương trình là:
có phương trình là:
Do đường thẳng cần tìm vuông góc với mặt phẳng
nên vectơ pháp tuyến của (P) là
cũng là vectơ chỉ phương của
.
Mặt khác đi qua điểm
nên phương trình chính tắc của
là:
Trong không gian với hệ tọa độ ![]() , đường thẳng đi qua điểm
, đường thẳng đi qua điểm ![]() và song song với trục
và song song với trục ![]() có phương trình tham số là:
có phương trình tham số là:
Gọi là đường thẳng cần tìm.
Ta có nên
có vectơ chỉ phương là
.
Do đó .
Cho 2 đường thẳng  và
và 
Mặt phẳng (P) chứa (d) và song song với ![]() có phương trình tổng quát :
có phương trình tổng quát :
Phương trình (d) cho và vectơ chỉ phương của (d) là:
Phương trình cho vectơ chỉ phương của
là :
Gọi là điểm bất kỳ thuộc mặt phẳng (P) thì :
Câu hỏi này cho ta thấy mối quan hệ giữa đường thẳng và mặt phẳng, từ 2 đường thảng ta có thể viết PT được của 1 mp.
Trong không gian ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() có các vectơ pháp tuyến là
có các vectơ pháp tuyến là ![]() . Góc
. Góc ![]() là góc giữa hai mặt phẳng đó
là góc giữa hai mặt phẳng đó ![]() là biểu thức nào sau đây?
là biểu thức nào sau đây?
Theo công thức góc giữa hai mặt phẳng ta có:
Trong không gian với hệ toạ độ ![]() , cho điểm
, cho điểm ![]() . Gọi
. Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên trục
trên trục ![]() . Phương trình nào dưới đây là phương trình mặt cầu tâm
. Phương trình nào dưới đây là phương trình mặt cầu tâm ![]() bán kính
bán kính ![]() ?
?
Hình chiếu vuông góc của trên
là:
Suy ra phương trình mặt cầu tâm bán kính
là:
.
Trong không gian ![]() cho hai mặt phẳng
cho hai mặt phẳng ![]() . Góc giữa hai mặt phẳng
. Góc giữa hai mặt phẳng ![]() bằng:
bằng:
Ta có: có 1 vectơ pháp tuyến là
có 1 vectơ pháp tuyến là
Khi đó:
Trong không gian tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() . Gọi
. Gọi ![]() là góc giữa đường thẳng
là góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có: có một vectơ chỉ phương là
,
có một vectơ pháp tuyến là
.
Từ đó:
Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]() . Vectơ nào trong các vectơ dưới đây không phải là vectơ chỉ phương của đường thẳng
. Vectơ nào trong các vectơ dưới đây không phải là vectơ chỉ phương của đường thẳng ![]() ?
?
Đường thẳng có 1 vectơ chỉ phương là
. Do đó vectơ
không là vectơ chỉ phương của
.
Cho hai điểm ![]() và mặt phẳng
và mặt phẳng ![]() Mặt phẳng
Mặt phẳng ![]() chứa hai điểm A,B và vuông góc với mặt phẳng
chứa hai điểm A,B và vuông góc với mặt phẳng ![]() có phương trình:
có phương trình:
Theo đề bài, ta có: ;
Suy ra ;
có vectơ pháp tuyến
Ta có cùng phương với vectơ
Chọn làm 1 vectơ pháp tuyến cho mặt phẳng
.
Phương trình mặt phẳng có dạng:
Mặt phẳng :
Cho ![]() và mặt phẳng
và mặt phẳng ![]() . Mặt phẳng
. Mặt phẳng ![]() song song với mặt phẳng
song song với mặt phẳng ![]() và
và ![]() cách điểm
cách điểm ![]() một khoảng bằng
một khoảng bằng ![]() . Phương trình mặt phẳng
. Phương trình mặt phẳng ![]() là:
là:
Vì
Mà
Vậy .
Trong không gian ![]() , có tất cả bao nhiêu giá trị nguyên của tham số
, có tất cả bao nhiêu giá trị nguyên của tham số ![]() để
để ![]() là một phương trình mặt cầu
là một phương trình mặt cầu
Phương trình đã cho là phương trình mặt cầu khi và chỉ khi
Theo bài ra
Vậy có tất cả 7 giá trị nguyên của tham số m thỏa mãn yêu cầu đề bài.
Viết phương trình tổng quát của mặt phẳng ![]() cắt hai trục
cắt hai trục ![]() và
và ![]() tại và tạo với mặt phẳng
tại và tạo với mặt phẳng ![]() một góc
một góc ![]() .
.
Gọi là giao điểm của
và trục
Vecto pháp tuyến của là:
Vecto pháp tuyến của là:
Gọi là góc tạo bởi và
Vậy có hai mặt phẳng:
Trong không gian với hệ tọa độ ![]() cho điểm
cho điểm ![]() và mặt phẳng
và mặt phẳng ![]() . Đường thẳng
. Đường thẳng ![]() đi qua
đi qua ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() cắt
cắt ![]() tại điểm
tại điểm ![]() . Điểm
. Điểm ![]() thay đổi trong
thay đổi trong ![]() sao cho
sao cho ![]() luôn nhìn đoạn
luôn nhìn đoạn ![]() dưới góc
dưới góc ![]() . Khi độ dài
. Khi độ dài ![]() lớn nhất, đường thẳng
lớn nhất, đường thẳng ![]() đi qua điểm nào trong các điểm sau?
đi qua điểm nào trong các điểm sau?
Hình vẽ minh họa
Phương trình
Đường thẳng d cắt P tại B(−2; −2; 1).
Gọi H là hình chiếu của A lên (P).
Ta có: H(−3; −2; −1).
Vì MB ⊥ MA; MB ⊥ AH nên MB ⊥ MH suy ra MB ≤ BH.
Do đó: MB lớn nhất bằng BH khi M ≡ H
Vậy MB đi qua B, nhận là vectơ chỉ phương.
Phương trình do đó MB đi qua điểm
.
Cho hình chóp ![]() có đáy ABC là tam giác vuông cân tại B, . Cạnh bên , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp
có đáy ABC là tam giác vuông cân tại B, . Cạnh bên , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp ![]() là:
là:
Gọi M là trung điểm AC, suy ra
Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.
Ta có , suy ra tam giác SAC đều.
Gọi G là trọng tâm , suy ra
. (1)
Tam giác ABC vuông tại B, có M là trung điểm cạnh huyền AC nên M là tâm đường tròn ngoại tiếp tam giác ABC.
Lại có nên SM là trục của tam giác ABC.
Mà G thuộc SM nên suy ra .
Từ (1) và (2), suy ra hay G là tâm mặt cầu ngoại tiếp khối chóp
.
Bán kính mặt cầu .
Trong không gian tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() và đường thẳng
và đường thẳng ![]() , sin của góc giữa đường thẳng
, sin của góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng:
bằng:
Mặt phẳng có một vectơ pháp tuyến là
Đường thẳng có một vectơ chỉ phương là
Gọi α là góc giữa đường thẳng d và mặt phẳng (P):
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng ![]() đi qua
đi qua ![]() và vuông góc với đường thẳng
và vuông góc với đường thẳng ![]() .
.
Mặt phẳng có một véctơ pháp tuyến
Phương trình mặt phẳng là:
hay
.
Trong hệ tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() và ba điểm
và ba điểm ![]() . Điểm M ∈ (α) sao cho
. Điểm M ∈ (α) sao cho ![]() đạt giá trị nhỏ nhất. Khẳng định nào sau đây đúng?
đạt giá trị nhỏ nhất. Khẳng định nào sau đây đúng?
Xét điểm I(a; b; c) thỏa mãn:
Khi đó
Khi đó:
Do đó đạt giá trị nhỏ nhất thì M là hình chiếu của I trên mặt phẳng
.
Do là hình chiếu của I trên mặt phẳng
nên ta có:
Vậy .
Trong không gian với hệ tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() . Gọi ∆’ là đường thẳng đối xứng với đường thẳng ∆ qua (Oxy). Tìm một vectơ chỉ phương của đường thẳng ∆’.
. Gọi ∆’ là đường thẳng đối xứng với đường thẳng ∆ qua (Oxy). Tìm một vectơ chỉ phương của đường thẳng ∆’.
Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm A(4; 11; 0).
Ta thấy B(1; 2; 3) ∈ ∆ và B’(1; 2; −3) là điểm đối xứng của điểm B qua mặt phẳng (Oxy).
Đường thẳng ∆’ đi qua các điểm A, B’.
Ta có , từ đó suy ra
là một vectơ chỉ phương của đường thẳng ∆’.
Điều kiện để ![]() là một mặt cầu là:
là một mặt cầu là:
Theo đề bài, ta có:
có dạng:
Như vậy, (S) là mặt cầu
