Lớp 10 Toán 10 - Chân trời sáng tạo

Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn

Mô tả thêm: Đề kiểm tra 1 tiết Toán 10 Bất phương trình bậc hai một ẩn gồm 40 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Chân trời sáng tạo.
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Biết phương trình \sqrt{x^{2} - 3x + 3} + \sqrt{x^{2} - 3x + 6} =3 có hai nghiệm x1, x2 (x1<x2) . Khẳng định nào sau đây là đúng?

    Đặt t = x2 − 3x + 3, ta có: t = \left( x - \frac{3}{2} ight)^{2}+ \frac{3}{4} \geq \frac{3}{4}.

    Do đó điều kiện cho ẩn phụ t là t \geq \frac{3}{4}.

    Khi đó phương trình trở thành:

    \sqrt{t} + \sqrt{t + 3} = 3\Leftrightarrow t + t + 3 +2\sqrt{t(t + 3)} = 9 ⇔ \sqrt{t(t + 3)} = 3 - t

    \Leftrightarrow \left\{ \begin{matrix}3 - t \geq 0 \\t(t + 3) = (3 - t)^{2} \\\end{matrix} ight. ⇔ \left\{ \begin{matrix}t \leq 3 \\t = 1 \\\end{matrix} ight.  ⇔ t = 1(thỏa mãn)

     ⇒ x2 − 3x + 3 = 1⇔ \left\lbrack \begin{matrix}x = 1 = x_{1} \\x = 2 = x_{2} \\\end{matrix} ight.\ \Rightarrow 2x_{1} = x_{2}.

  • Câu 2: Thông hiểu

    Cho bất phương trình x^{2}−8x+7≥0 . Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.

     Ta có: x^{2}−8x+7≥0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \le 1}\\{x \ge 7}\end{array}} ight.. Suy ra S=[-\infty;1) \cup [7;+\infty).

    Nhận xét: [6;+\infty) không thuộc S.

  • Câu 3: Nhận biết

    Tam thức bậc hai f(x) = 4x2 − 12x + 9 nhận giá trị âm khi và chỉ khi

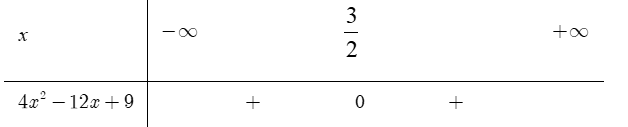
    Chọn Ta có: f(x) = 4x^{2} - 12x + 9 = 0 \Leftrightarrow x = \frac{3}{2}

    Dựa vào bảng xét dấu thì ta thấy không có giá trị x nào để f(x) < 0.

  • Câu 4: Thông hiểu

    Nghiệm của phương trình \frac{x^{2}-4x+3}{\sqrt{x-1}}=\sqrt{x-1} là:

     Điều kiện: x>1.

    Ta có: \frac{x^{2}-4x+3}{\sqrt{x-1}}=\sqrt{x-1} \Rightarrow x^2-4x+3=x-1\Leftrightarrow x^2-5x+4=0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 4}\end{array}} ight..

    Loại x=1. Do đó S=\{4\}.

  • Câu 5: Nhận biết

    Tam thức bậc hai f(x) = x^{2} + \left( \sqrt{5} - 1 ight)x - \sqrt{5} nhận giá trị dương khi và chỉ khi

    f(x) = x^{2} + \left( \sqrt{5} - 1 ight)x - \sqrt{5} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - \sqrt{5} \\ \end{matrix} ight.

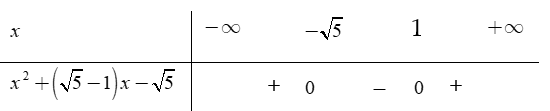
    Dựa vào bảng xét dấu, ta chọn đáp án x \in \left( - \infty; - \sqrt{5} ight) \cup (1; + \infty).

  • Câu 6: Vận dụng cao

    Tất cả các giá trị của tham số m để các nghiệm của phương trình \sqrt{x+1}-2=0\;(1) cũng là nghiệm của phương trình x2 − 2mx − m2 − 2 = 0 (2) là:

    \sqrt{x + 1} = 2 \Leftrightarrow x + 1 = 4 \Leftrightarrow x = 3

    Do đó, để mọi nghiệm của (1) cũng là nghiệm của (2) điều kiện là x = 3 cũng là nghiệm của (2), tức là: 9 - 6m - m^{2} - 2 = 0 \Leftrightarrow m^{2} + 6m - 7 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ m = - 7 \\ \end{matrix} ight..

  • Câu 7: Thông hiểu

    Cho f(x) =  − 2x2 + (m+2)x + m − 4. Tìm m để f(x) âm với mọi a, b, c > 0.

    Ta có f(x)<0,\forall x\in R\Leftrightarrow(m+2)^2+8(m-4)<0

    \Leftrightarrow m^2+12m-28<0\Leftrightarrow-14<m<2.

  • Câu 8: Thông hiểu

    Tìm tập xác định D của hàm số y = \sqrt{2x^{2} - 5x + 2}.

    Điều kiện 2x^{2} - 5x + 2 \geq 0 \Leftrightarrow \left\lbrack \begin{matrix} x \geq 2 \\ x \leq \frac{1}{2} \\ \end{matrix} ight..

    Vậy tập xác định của hàm số là \left( - \infty;\frac{1}{2} ightbrack \cup \lbrack 2; + \infty).

  • Câu 9: Thông hiểu

    Tìm m để f(x) = x2 − 2(2m−3)x + 4m − 3 > 0,    ∀x ∈ ℝ?

    f(x) = x2 − 2(2m−3)x + 4m − 3 > 0, ∀x ∈ ℝ⇔Δ < 0 ⇔ 4m2 − 16m + 12 < 0 ⇔ 1 < m < 3.

  • Câu 10: Vận dụng

    Tìm các giá trị của m để biểu thức sau luôn âm: f(x) = mx2 − x − 1.

    Với m = 0 thì f(x) =  − x − 1 lấy cả giá trị dương (chẳng hạn f(−2) = 1) nên m = 0 không thỏa mãn yêu cầu bài toán

    Với m ≠ 0 thì f(x) = mx2 − x − 1 là tam thức bậc hai do đó f(x) < 0,\ \ \forall x \Leftrightarrow \left\{ \begin{matrix} a = m < 0 \\ \Delta = 1 + 4m < 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m < 0 \\ m > - \frac{1}{4} \\ \end{matrix} \Leftrightarrow - \frac{1}{4} < m < 0 ight.

    Vậy với - \frac{1}{4} < m < 0 thì biểu thức f(x) luôn âm.

  • Câu 11: Vận dụng

    Tìm tất cả các giá trị thực của tham số m để bất phương trình (2m2−3m−2)x2 + 2(m−2)x − 1 ≤ 0 có tập nghiệm là ℝ.

    Xét 2m^{2} - 3m - 2 = 0 \Leftrightarrow m = - \frac{1}{2}hoặc m = 2

    • Khi m = - \frac{1}{2} thì bất phương trình trở thành x \geq - \frac{1}{5} nên không có nghiệm đúng với mọi x.

    • Khi m = 2 thì bất phương trình trở thành  − 1 ≤ 0 nên có nghiệm đúng với mọi x.

    • Khi \left\{ \begin{matrix} m eq - \frac{1}{2} \\ m eq 2 \\ \end{matrix} ight. thì yêu cầu bài toán

     ⇔ (2m2−3m−2)x2 + 2(m−2)x − 1 ≤ 0  ∀x ∈ ℝ

    \Leftrightarrow \left\{ \begin{matrix} \Delta' \leq 0 \\ a < 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} 3m^{2} - 7m + 2 \leq 0 \\ 2m^{2} - 3m - 2 < 0 \\ \end{matrix} ight.\ ight.

    \Leftrightarrow \left\{ \begin{matrix} \frac{1}{3} \leq m \leq 2 \\ - \frac{1}{2} < m < 2 \\ \end{matrix} \Leftrightarrow \frac{1}{3} \leq m < 2 ight.

    Kết hợp hai trường hợp ta được \frac{1}{3} \leq m \leq 2 là giá trị cần tìm.

  • Câu 12: Nhận biết

    Nghiệm của phương trình \sqrt{-10x+10}=x-1 là:

     Ta có: \sqrt{-10x+10}=x-1 \Rightarrow -10x+10=x^2-2x+1\Leftrightarrow x^2+8x-9=0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 9}\end{array}} ight..

    Thử lại thấy x=9 không thỏa mãn. Do đó x=1.

  • Câu 13: Vận dụng cao

    Tập tất cả các giá trị của tham số m để phương trình \sqrt{x^{2} - 2mx + 1} = m - 2 có nghiệm thực là

    * Với m < 2 ⇒ phương trình vô nghiệm

    * Với m ≥ 2, \sqrt{x^2-2mx+1}=m-2

    \Leftrightarrow x^2-2mx+1=m^2-4m+4

    \Leftrightarrow x^2-2mx-m^2+4m-3=0.

    Phương trình có nghiệm Δ′ = 2(m−1)2 + 1 > 0 đúng mọi m.

    Vậy m ≥ 2 là những giá trị cần tìm hay m thuộc [2;  + ∞).

  • Câu 14: Nhận biết

    Số nghiệm nguyên dương của phương trình \sqrt{x - 1} = x - 3 là

    \sqrt{x - 1} = x - 3 \Leftrightarrow\left\{ \begin{matrix}x \geq 3 \\x - 1 = (x - 3)^{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 3 \\x^{2} - 7x + 10 = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 3 \\\left\lbrack \begin{matrix}x = 2 \\x = 5 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Rightarrow x = 5.

    Vậy phương trình có một nghiệm nguyên dương.

  • Câu 15: Nhận biết

    Cho tam thức bậc hai f(x) = {x^2} - 10x + 2. Kết luận nào sau đây đúng?

    Ta có:

    \begin{matrix}f\left( { - 2} ight) = {\left( { - 2} ight)^2} - 10.\left( { - 2} ight) + 2 = 26 > 0 \hfill \\ f\left( 1 ight) = {\left( 1 ight)^2} - 10.\left( 1 ight) + 2 = - 7 < 0 \hfill \\ \end{matrix}

    Vậy khẳng định đúng là f(–2) > 0.

  • Câu 16: Vận dụng

    Tìm tất cả các giá trị của tham số m để phương trình \sqrt{2x + m} = x - 1\ \ (*) có hai nghiệm phân biệt lớn hơn 1?

    Phương trình

    \sqrt{2x + m} = x - 1

    \Leftrightarrow \left\{ \begin{matrix} x - 1 \geq 0 \\ 2x + m = (x - 1)^{2} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 1 \\ x^{2} - 4x + 1 - m = 0\ (**) \\ \end{matrix} ight.

    Phương trình (*) có hai nghiệm phân biệt lớn hơn 1 \Leftrightarrow (**) có hai nghiệm phân biệt lớn hơn 1.

    \Leftrightarrow \left\{ \begin{matrix} \Delta > 0 \\ 1 < x_{1} < x_{2} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \Delta > 0 \\ 0 < x_{1} - 1 < x_{2} - 1 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} 3 + m > 0 \\ \left( x_{1} - 1 ight).\left( x_{2} - 1 ight) > 0 \\ x_{1} + x_{2} > 2 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m > - 3 \\ x_{1}x_{2} - \left( x_{1} + x_{2} ight) + 1 > 0 \\ x_{1} + x_{2} > 2 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m > - 3 \\ 1 - m - 4 + 1 > 0 \\ 4 > 2 \\ \end{matrix} ight.\ \Leftrightarrow - 3 < m < 2

  • Câu 17: Thông hiểu

    Phương trình\frac{x^{2}-4x-2}{\sqrt{x-2}}=\sqrt{x-2} có tất cả bao nhiêu nghiệm?

     Điều kiện: x>2.

    Ta có: \frac{x^{2}-4x-2}{\sqrt{x-2}}=\sqrt{x-2} \Rightarrow x^2-4x-2=x-2x^2-5x=0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 5}\end{array}} ight..

    Loại x=0. Do đó phương trình có 1 nghiệm.

  • Câu 18: Nhận biết

    Giải bất phương trình x(x+5)≤2(x^{2}+2)

     Ta có: x(x+5)≤2(x^{2}+2) \Leftrightarrow -x^2+5x-4 \le 0\Leftrightarrow x\in (-∞;1]\cup [4;+∞).

  • Câu 19: Thông hiểu

    Phương trình \sqrt{3x} + \sqrt{2x - 2} = \sqrt{1 - x} +2 có bao nhiêu nghiệm?

    ĐKXĐ: \left\{ \begin{matrix}3x \geq 0 \\2x - 2 \geq 0 \\1 - x \geq 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\x \geq 1 \\x \leq 1 \\\end{matrix} ight.\ \Leftrightarrow x = 1.

    Thay x = 1 vào \sqrt{3x} + \sqrt{2x - 2} = \sqrt{1 - x} +2, ta được: \sqrt{3} = 2 .

    Vậy phương trình vô nghiệm.

  • Câu 20: Vận dụng

    Tổng các nghiệm của phương trình x(x + 5) = 2\sqrt[3]{x^{2} + 5x - 2} - 2 là:

    Đặt t = \sqrt[3]{x^{2} + 5x - 2}. Phương trình trở thành:

    t3 − 2t + 4 = 0 ⇔ (t+2)(t2−2t+2) = 0 ⇔ t =  − 2

    Ta được

    \sqrt[3]{x^{2} + 5x - 2} = - 2\Leftrightarrow x^{2} + 5x + 6 = 0 \Leftrightarrow \left\lbrack\begin{matrix}x = - 2 \\x = - 3 \\\end{matrix} ight..

    Tổng các nghiệm của phương trình là  − 5.

  • Câu 21: Thông hiểu

    Số giá trị nguyên của x để tam thức f(x)=2x^{2}−7x−9 nhận giá trị âm là:

     Ta có: \Delta >0 và a=2>0.

    Phương trình f(x)=0 có hai nghiệm x=-1;x=\frac92.

    Do đó f(x)<0 \Leftrightarrow -1 < x < \frac92 \Leftrightarrow x=\{0;1;2;3;4\} (5 giá trị).

  • Câu 22: Nhận biết

    Phương trình \sqrt{4x^{2}-3}=x có nghiệm là:

    Điều kiện: 4{x^2} - 3 \geqslant 0

    Phương trình tương đương:

    \begin{matrix} \sqrt {4{x^2} - 3} = x \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {4{x^2} - 3 = {x^2}} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {3{x^2} = 3} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {\left[ {\begin{array}{*{20}{c}} {x = - 1\left( {ktm} ight)} \\ {x = 1\left( {tm} ight)} \end{array}} ight.} \end{array}} ight. \hfill \\ \end{matrix}

    Kết hợp với điều kiện ra được: x=1 thỏa mãn điều kiện

    Vậy phương trình có nghiệm x=1

  • Câu 23: Thông hiểu

    Tập nghiệm của phương trình: \sqrt{3-x+x^{2}}-\sqrt{2+x-x^{2}}=1 là:

    Điều kiện: \left\{ {\begin{array}{*{20}{c}} {3 - x + {x^2} \geqslant 0} \\ {2 + x - {x^2} \geqslant 0} \end{array}} ight. => x \in \left[ { - 1,2} ight]

    Phương trình tương đương

    \begin{matrix} \sqrt {3 - x + {x^2}} - \sqrt {2 + x - {x^2}} = 1 \hfill \\ \Leftrightarrow \sqrt {3 - x + {x^2}} - 2 + 1 - \sqrt {2 + x - {x^2}} = 0 \hfill \\ \Leftrightarrow \dfrac{{{x^2} - x - 1}}{{\sqrt {3 - x + {x^2}} + 2}} + \dfrac{{{x^2} - x - 1}}{{1 + \sqrt {2 + x - {x^2}} }} = 0 \hfill \\ \Leftrightarrow \left( {{x^2} - x - 1} ight)\left( {\dfrac{1}{{\sqrt {3 - x + {x^2}} + 2}} + \dfrac{1}{{1 + \sqrt {2 + x - {x^2}} }}} ight) = 0 \hfill \\ \end{matrix}

    Ta có: \frac{1}{{\sqrt {3 - x + {x^2}} + 2}} + \frac{1}{{1 + \sqrt {2 + x - {x^2}} }} > 0,\forall x \in \left[ { - 1,2} ight]

    \begin{matrix} \Leftrightarrow {x^2} - x - 1 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{{1 - \sqrt 5 }}{2}} \\ {x = \dfrac{{1 + \sqrt 5 }}{2}} \end{array}} ight.\left( {tm} ight) \hfill \\ \end{matrix}

    Vậy tập nghiệm của phương trình là: \left\{ {\frac{{1 + \sqrt 5 }}{2};\frac{{1 - \sqrt 5 }}{2}} ight\}

  • Câu 24: Vận dụng

    Số nghiệm của phương trình (3x + 1)\sqrt{x^{2} + 3} = 3x^{2} + 2x + 3 là:

    Ta thấy x = - \frac{1}{3} không là nghiệm của phương trình

    Xét x eq - \frac{1}{3}, phương trình đã cho \Leftrightarrow \sqrt{x^{2} + 3}= \frac{3x^{2} + 2x + 3}{3x + 1}

    Đến đây, chú ý 3x^{2} + 2x + 3 = 3(x +\frac{1}{3})^{2} + \frac{8}{3} > 0

    Nên phương trình có nghiệm phải thỏa mãn x> - \frac{1}{3} \Rightarrow \sqrt{x^{2} + 3} + 2x > 0

    Do đó phương trình đã cho\Leftrightarrow\sqrt{x^{2} + 3} - 2x = \frac{3x^{2} + 2x + 3}{3x + 1} - 2x

    \Leftrightarrow \frac{x^{2} + 3 -4x^{2}}{\sqrt{x^{2} + 3} + 2x} = \frac{3x^{2} + 2x + 3 - 6x^{2} - 2x}{3x+ 1}

    \Leftrightarrow \frac{3\left( 1 - x^{2}ight)}{\sqrt{x^{2} + 3} + 2x} = \frac{3\left( 1 - x^{2} ight)}{3x +1}

    \Leftrightarrow \left\lbrack\begin{matrix}x^{2} = 1 \\\sqrt{x^{2} + 3} + 2x = 3x + 1 \\\end{matrix} ight.

    Nhưng x =  − 1 không thoả mãn x > - \frac{1}{3} nên phương trình có nghiệm x = 1

    * TH2: \sqrt{x^{2} + 3} + 2x = 3x + 1\Leftrightarrow \sqrt{x^{2} + 3} = x + 1

    \Leftrightarrow \left\{ \begin{matrix}x \geq - 1 \\x^{2} + 3 = x^{2} + 1 + 2x \\\end{matrix} ight.\ \ \ \Leftrightarrow x = 1 (thỏa mãn)

    Vậy phương trình có nghiệm duy nhất x = 1.

  • Câu 25: Thông hiểu

    Tam thức f(x) =  − 2x2 + (m−2)x − m + 4 không dương với mọi x khi:

    f(x) \leq 0,\ \forall x\mathbb{\in R \Leftrightarrow}\left\{ \begin{matrix} a < 0 \\ \Delta' \leq 0 \\ \end{matrix} ight.\ \Leftrightarrow m^{2} - 12m + 36 \leq 0\ \ \Leftrightarrow \ \ m = 6.

  • Câu 26: Nhận biết

    Tổng các nghiệm của phương trình \sqrt{2x - 1} + x^{2} - 3x + 1 = 0 là :

    Ta có \sqrt{2x - 1} + x^{2} - 3x + 1 = 0\Leftrightarrow \sqrt{2x - 1} = - x^{2} + 3x - 1

    \Leftrightarrow \left\{ \begin{matrix}- x^{2} + 3x - 1 \geq 0 \\2x - 1 = \left( - x^{2} + 3x - 1 ight)^{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}- x^{2} + 3x - 1 \geq 0 \\(x - 1)^{2}(x^{2} - 4x + 2) = 0 \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}- x^{2} + 3x - 1 \geq 0 \\\left\lbrack \begin{matrix}x = 1 \\x^{2} - 4x + 2 = 0 \\\end{matrix} ight.\ \\\end{matrix} ight. \Leftrightarrow \left\{ \begin{matrix}- x^{2} + 3x - 1 \geq 0 \\\left\lbrack \begin{matrix}x = 1 \\x = 2 \pm \sqrt{2} \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}x = 1 \\x = 2 - \sqrt{2} \\\end{matrix} ight.

    Phương trình có nghiệm là x = 1 và x = 2 - \sqrt{2}.

    Vậy tổng các nghiệm của phương trình là 1+ 2 - \sqrt{2} = 3 - \sqrt{2}.

  • Câu 27: Nhận biết

    Tam thức f(x) = x2 − 2x − 3 nhận giá trị dương khi và chỉ khi

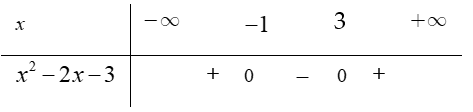
    Ta có: f(x) = x^{2} - 2x - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, chọn đáp án x ∈ (−∞;−1) ∪ (3;+∞).

  • Câu 28: Thông hiểu

    Tam thức bậc hai .

    Ta có .

    Bảng xét dấu

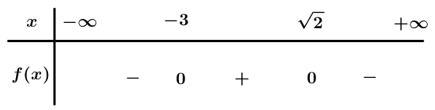
    Dựa vào bảng xét dấu .

  • Câu 29: Nhận biết

    Số nghiệm của phương trình x = \sqrt{\sqrt{3x^{2} + 1} - 1} là bao nhiêu?

    x = \sqrt{\sqrt{3x^{2} + 1} - 1}\Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\x^{2} = \sqrt{3x^{2} + 1} - 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\\sqrt{3x^{2} + 1} = x^{2} + 1 \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\3x^{2} + 1 = (x^{2} + 1)^{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\x^{4} - x^{2} = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\x^{2}\left( x^{2} - 1 ight) = 0 \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ \left\lbrack \begin{matrix} x = 0 \\ x = \pm 1 \\ \end{matrix} ight.\ \\ \end{matrix} \Leftrightarrow ight.\ \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight. .

    Vậy phương trình có hai nghiệm.

  • Câu 30: Nhận biết

    Số nghiệm của phương trình x - \sqrt{3x + 4} = 2 là:

    x - \sqrt{3x + 4} = 2 \Leftrightarrow\sqrt{3x + 4} = x - 2\Leftrightarrow \left\{ \begin{matrix}x - 2 \geq 0 \\3x + 4 = (x - 2)^{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\3x + 4 = x^{2} - 4x + 4 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\x^{2} - 7x = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\\left\lbrack \begin{matrix}x = 0 \\x = 7 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow x = 7.

    Vậy phương trình có 1 nghiệm.

  • Câu 31: Thông hiểu

    Số nghiệm của phương trình 3x + \sqrt{x - 8} = \sqrt{4 - x} là:

    Xét phương trình: 3x + \sqrt{x - 8} =\sqrt{4 - x}.

    Điều kiện: \left\{ \begin{matrix}x - 8 \geq 0 \\4 - x \geq 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 8 \\x \leq 4 \\\end{matrix} ight.\ \Leftrightarrow x \in \varnothing.

    Vậy phương trình vô nghiệm.

  • Câu 32: Nhận biết

    Cho f(x) = x2 − 4x + 3. Trong các mệnh đề sau, mệnh đề đúng là:

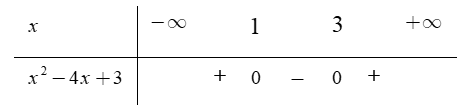
    f(x) = x^{2} - 4x + 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu thì f(x) ≤ 0, ∀x ∈ [ 1; 3 ].

  • Câu 33: Nhận biết

    Tam thức bậc hai f(x) =  − x2 + 3x − 2 nhận giá trị không âm khi và chỉ khi

    f(x) = - x^{2} + 3x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 2 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, ta chọn đáp ánx ∈ [1; 2] .

  • Câu 34: Nhận biết

    Cho tam thức bậc hai f(x) = 5x − x2 − 6. Tìm x để f(x) ≥ 0.

    f(x) = 5x - x^{2} - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, ta chọn đáp án x ∈ [2; 3].

  • Câu 35: Nhận biết

    Tìm tập nghiệm của phương trình \sqrt{4x+1}+5=0

     Nhận xét: \sqrt{4x+1} \ge 0 \Leftrightarrow \sqrt{4x+1}+5 >0. 

    Do đó \sqrt{4x+1}+5=0 vô lí. 

    Vậy S=\varnothing.

  • Câu 36: Vận dụng

    Tìm m để g(x) = (2m2+m−6)x2 + (2m−3)x − 1 không dương.

    Xét 2m^{2} + m - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = - 2 \\ m = \frac{3}{2} \\ \end{matrix} ight.

    +)m = - 2 \Rightarrow g(x) = - 7x - 1 > 0 \Leftrightarrow x < - \frac{1}{7} (không thỏa mãn yêu cầu bài toán)

    +) m = \frac{3}{2} \Rightarrow g(x) = 0 (không thỏa mãn)

    Xét 2m^{2} + m - 6 eq 0 \Leftrightarrow \left\{ \begin{matrix} m eq - 2 \\ m eq \frac{3}{2} \\ \end{matrix} ight.

    g(x) \leq 0,\ \ \forall x \Leftrightarrow \left\{ \begin{matrix} a = 2m^{2} + m - 6 < 0 \\ \Delta' = 12m^{2} - 8m - 15 \leq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} - 2 < m < \frac{3}{2} \\ - \frac{5}{6} \leq m \leq \frac{3}{2} \\ \end{matrix} ight.\ \Leftrightarrow - \frac{5}{6} \leq m < \frac{3}{2}

  • Câu 37: Nhận biết

    Tổng các bình phương của các nghiệm của phương trình(x - 1)(x - 3) + 3\sqrt{x^{2} - 4x + 5} - 2 = 0 bằng bao nhiêu?

    Ta có (x - 1)(x - 3) + 3\sqrt{x^{2} - 4x + 5} - 2 = 0

    \Leftrightarrow x^{2} - 4x + 5 +3\sqrt{x^{2} - 4x + 5} - 4 = 0\Leftrightarrow \sqrt{x^{2} - 4x + 5} =1

    \Leftrightarrow x^{2} - 4x + 5 = 1 \Leftrightarrow x^{2} - 4x + 4 = 0 \Leftrightarrow x = 2.

    Tổng các bình phương của các nghiệm của phương trình là 4.

  • Câu 38: Vận dụng cao

    Phương trình x^{2} = \sqrt{2 - x} + 2 có mấy nghiệm nguyên ?

    Đặt t = \sqrt{2 - x}\ \ \ (t \geq 0). Ta có hệ phương trình:

    \left\{ \begin{matrix} x^{2} = t + 2 \\ t^{2} = - x + 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} t = - x \\ t = x - 1 \\ \end{matrix} ight.

    Với t =  − x ta được \left\lbrack \begin{matrix} x = 1 \Rightarrow t = - 1(L) \\ x = - 2 \Rightarrow t = 2(TM) \\ \end{matrix} ight.

    Với t = x − 1 ta được \left\lbrack \begin{matrix} x = \frac{1 + \sqrt{5}}{2} \Rightarrow t = \frac{\sqrt{5} - 1}{2}(TM) \\ x = \frac{1 - \sqrt{5}}{2} \Rightarrow t = \frac{- \sqrt{5} - 1}{2}(L) \\ \end{matrix} ight.

    Vậy phương trình có 2 nghiệm x =  − 2 và x = \frac{1 + \sqrt{5}}{2}.

  • Câu 39: Nhận biết

    Tam thức bậc hai f(x) =  − x2 + 5x − 6 nhận giá trị dương khi và chỉ khi

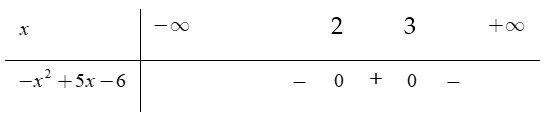
    f(x) = - x^{2} + 5x - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, ta chọn đáp án x ∈ (2;3).

  • Câu 40: Nhận biết

    Tìm khẳng định đúng trong các khẳng định sau?

    Tam thức bậc 2 là biểu thức f(x) có dạng  ax2+ bx + c (a≠0).

    f(x) = 3x2 − 5 là tam thức bậc 2 với a = 3, b = 0, c =  − 5.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 9 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập