Lớp 10 Toán 10 - Kết nối tri thức

Đề kiểm tra 45 phút Đại số 10 Chương 1 Kết nối tri thức

Mô tả thêm: Đề kiểm tra 1 tiết Toán 10 Mệnh đề và tập hợp gồm 40 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Kết nối tri thức.
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng cao

    Cho hai tập hợp khác rỗng A = (m - 1;4brack và B = ( - 2;2m + 2)với m\mathbb{\in R}. Tìm m để A \cap B eq \varnothing.

    \Leftrightarrow \left\{ \begin{matrix} m - 1 < 4 \\ 2m + 2 > - 2 \\ \end{matrix} ight.\ \Leftrightarrow - 2 < m < 5(*)

    Ta có A \cap B = \varnothing \Leftrightarrow 2m + 2 \leq m - 1 \Leftrightarrow m \leq - 3\ (**)

    Từ (*) và (**) suy ra A \cap B eq \varnothing \Leftrightarrow - 2 < m < 5.

  • Câu 2: Nhận biết

    Cho A = \left\{ 0;2;3;4 ight\}, B = \left\{ 2;3;4;5;6 ight\}. Tập hợp A\setminus B bằng

    Tập hợp A\backslash B gồm những phần tử thuộc A nhưng không thuộc B

    \Rightarrow A\backslash B = \left\{ 0 ight\}.

  • Câu 3: Nhận biết

    Cho A = \left\{ 0;1;2;3;4 ight\}, B = \left\{ 2;3;4;5;6 ight\}. Tập hợp B\backslash A bằng

    Tập hợp B\backslash A gồm những phần tử thuộc B nhưng không thuộc A

    \Rightarrow B\backslash A = \left\{ 5;6 ight\}.

  • Câu 4: Thông hiểu

    Trong các tập hợp sau, tập hợp nào bằng nhau:

    • A = \left \{ {0; 2; 4; 6; 8} ight \}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 2 và x < 12}

    => A = \left \{ {0; 2; 4; 6; 8} ight \}; B = \left \{ {0; 2; 4; 6; 8; 10} ight \}. Vậy tập hợp A không bằng tập hợp B.

    • A = {x| x ∈ \mathbb{ℕ}, x ⋮ 2 và 2< x < 6}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 4 và 1 < x < 5}

    => A = \left \{ {4} ight \} ; B = \left \{ {4} ight \}. Vậy tập hợp A bằng tập hợp B. Đáp án đúng

    • A = \left \{ {2; 4; 6; 8} ight \}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 2 và x < 10}

    => A = \left \{ {2; 4; 6; 8} ight \}; B =\left \{ {0; 2; 4; 6; 8} ight \}. Vậy tập hợp A không bằng tập hợp B.

    • A = {x| x ∈ \mathbb{ℕ}, x chia hết cho 3 và x < 12}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 4 và x < 12}

    => A = \left \{{0; 3; 6; 9} ight \}; B =\left \{ {0; 4; 8} ight \}. Vậy tập hợp A không bằng tập hợp B.

  • Câu 5: Nhận biết

    Tìm mệnh đề chứa biến.

    “x + 2 = 11.” là mệnh đề chứa biến.

  • Câu 6: Thông hiểu

    Số phần tử của tập hợp A = \left\{ k^{2} + 1|k \in \mathbb{Z,}|k| \leq 2 ight\} là

    Ta có: \left\{ \begin{matrix} \mathbf{k \in}\mathbf{Z} \\ \left| \mathbf{k} ight|\mathbf{\leq}\mathbf{2} \\ \end{matrix} ight.\ \mathbf{\Leftrightarrow k =}\left\{ \mathbf{\pm}\mathbf{2;}\mathbf{\pm}\mathbf{1;0} ight\}\mathbf{\Rightarrow A =}\left\{ \mathbf{5;2;1} ight\}

  • Câu 7: Thông hiểu

    Xác định A ∩ B trong trường hợp sau:

    \begin{matrix} A = \left\{ {(x;y)|x,y \in \mathbb{R},3x - y = 7} ight\} \hfill \\ B = \left\{ {(x;y)|x,y \in \mathbb{R},x - y = 1} ight\} \hfill \\ \end{matrix}

    Tập hợp A ∩ B là tập hợp cặp số (x; y) thỏa mãn hệ phương trình:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {3x - y = 7} \\ {x - y = 1} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = 3} \\ {y = 2} \end{array}} ight. \hfill \\ \Rightarrow \left( {x;y} ight) = \left( {3;2} ight) \hfill \\ \end{matrix}

    Vậy A \cap B = \left\{ {\left( {3;2} ight)} ight\}

  • Câu 8: Nhận biết

    Khẳng định nào đúng trong các khẳng định sau:

    Khẳng định đúng: "Nếu A ⊂ B và B ⊂ C thì A ⊂ C" 

  • Câu 9: Vận dụng cao

    Tìm tất cả các giá trị thực âm của tham số m để hai khoảng ( - \infty;2m) và \left( \frac{2}{m}; + \infty ight) có khoảng giao khác rỗng.

    Với m < 0 thì \frac{2}{m} luôn có nghĩa. 

    Giao của hai tập đã cho khác rỗng khi hai tập hợp này có phần tử chung 

    \Leftrightarrow 2m > \frac{2}{m} \Leftrightarrow 2m^{2} < 2 (vì m < 0) \Leftrightarrow 2(m - 1)(m + 1) < 0

    Vì m < 0 nên ta xét các trường hợp sau

    Nếu m < - 1 thì m + 1 < 0,m - 1 < 0 = > 2(m - 1)(m + 1) > 0

    Vậy m < - 1 không thỏa yêu cầu bài toán.

    Nếu −1 < m < 0 thì m + 1 > 0,m - 1 < 0 \Rightarrow 2(m - 1)(m + 1) < 0

    Vậy giá trị cần tìm của m là - 1 < m < 0.

  • Câu 10: Thông hiểu

    Khi x là số lẻ, mệnh đề nào sau đây là mệnh đề sai:

    Khi x là số lẻ => “x không chia hết cho 4” là mệnh đề đúng.

    Khi x là số lẻ “x không chia hết cho 3” và “x chia hết cho 3” là một khẳng định nhưng không xác định được tính hoặc đúng hoặc sai tùy theo giá trị của x => Không phải mệnh đề.

    Khi x là số lẻ “x chia hết cho 2” là mệnh đề sai.

  • Câu 11: Thông hiểu

    Cho mệnh đề A: “\forall x \in R,x^{2} - x + 7 < 0”. Mệnh đề phủ định của A là:

    Phủ định của \forall là \exists.

    Phủ định của < là \geq.

    Mệnh đề phủ định của A: \exists x \in R,x^{2} - \ x + 7 \geq 0.

  • Câu 12: Nhận biết

    Chọn phát biểu đúng về mệnh đề sau: "∀x ∈ \mathbb{N}, x^{2} <0"?

    Phát biểu đúng của mệnh đề "∀x ∈ \mathbb{N}, x^{2} <0" là: “Với mọi số tự nhiên x, bình phương của nó đều nhỏ hơn 0”.

  • Câu 13: Nhận biết

    Tìm mệnh đề trong các câu sau.

    Các câu “Hôm nay, trời đẹp quá!”, “Bạn ăn cơm chưa?”, “Mấy giờ rồi?” là các câu cảm thán hoặc nghi vấn nên không phải là mệnh đề.

    Chọn đáp án Paris là thủ đô của Đức.

  • Câu 14: Nhận biết

    Cho tập hợp A = \left\{ 2;4;6;9 ight\} và B = \left\{ 1;2;3;4 ight\}. Tập hợp A\backslash B bằng tập nào sau đây?

    Tập hợp A\backslash B gồm những phần tử thuộc A nhưng không thuộc B.

    \Rightarrow A\backslash B = \left\{ 6;9 ight\}.

  • Câu 15: Vận dụng

    Biết A là mệnh đề đúng, B là mệnh đề sai, C là mệnh đề đúng. Mệnh đề nào sau đây sai?

    Ta có: A là mệnh đề đúng, B là mệnh đề sai nên A \Rightarrow B là mệnh đề sai.

    C là mệnh đề đúng, A \Rightarrow B là mệnh đề sai nên C \Rightarrow (A \Rightarrow B)là mệnh đề sai.

    Chọn đáp án C \Rightarrow (A \Rightarrow B).

  • Câu 16: Nhận biết

    Kí hiệu C_{U}A có nghĩa là gì?

    Cho hai tập hợp A và U. Nếu A là tập con của U thì hiệu U\setminus A gọi là phần bù của A trong U, kí hiệu {C_U}A.

  • Câu 17: Thông hiểu

    Cho tập X = \left\{ 2,3,4 ight\}. Tập X có bao nhiêu tập hợp con?

    Tập X có 3 phần tử \Rightarrow số tập con của X bằng: 2^{3} = 8.

  • Câu 18: Nhận biết

    Cho mệnh đề: “Một tứ giác là hình thang cân khi và chỉ khi tứ giác đó có hai đường chéo bằng nhau”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?

     Mệnh đề tương đương với mệnh đề đã cho là: Điều kiện cần và đủ để một tứ giác có hai đường chéo bằng nhau là tứ giác đó là một hình thang cân.

  • Câu 19: Nhận biết

    Người ta thường kí hiệu tập hợp số như thế nào?

     Người ta thường kí hiệu các tập hợp số như sau:

    • \mathbb{ℕ} là tập hợp các số tự nhiên.
    • \mathbb{ℤ} là tập hợp các số nguyên.
    • \mathbb{ℝ} là tập hợp các số thực.
  • Câu 20: Thông hiểu

    Mệnh đề: " \exists x \in \mathbb{R},x^{2} > 33 " khẳng định là

    Mệnh đề: " \exists x \in \mathbb{R},x^{2} > 33 " khẳng định là có ít nhất một số thực mà bình phương của nó lớn hơn 33.

  • Câu 21: Nhận biết

    Cho mệnh đề P: “∆ABC cân tại A ⇔ AB = AC”. Chọn khẳng định đúng nhất trong các khẳng định sau?

     Vì AB = AC nên suy ra ∆ABC cân tại A.

    Vì ∆ABC cân tại A nên suy ra AB = AC.

    Do đó đáp án đúng là “∆ABC cân tại A” là điều kiện cần và đủ để “AB = AC”.

  • Câu 22: Thông hiểu

    Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 12,B = \{ n \in \mathbb{N} \mid n \leq 6\}, C = \{ n \in \mathbb{N} \mid 4 \leq n \leq 12\}. Mệnh đề nào sau đây là đúng?

    Liệt kê các phần tử của tập hợp đã cho ta có kết luận đúng là:

    A \cap (B \cup C) = A

  • Câu 23: Nhận biết

    Mệnh đề nào sau đây là mệnh đề tương đương?

    Mệnh đề tương đương là: “Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân”.

  • Câu 24: Thông hiểu

    Cho C_{R}A = ( -\infty;2) \cup \lbrack 6; + \infty) và C_{R}B = \lbrack 5;9). Tập hợp X = A \cap B là

    A = \lbrack 2;6),B = ( - \infty;5) \cup\lbrack 9; + \infty).

    Suy ra X = A \cap B = \lbrack2;5).

  • Câu 25: Nhận biết

    Vùng tô đậm thể hiện mối quan hệ gì giữa 2 tập hợp A, B:

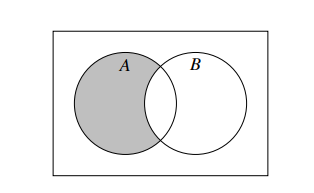
    Tìm mối quan hệ giữa hai tập hợp

    Hình vẽ mô tả các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B

    => Vùng tô đậm thể hiện A\setminus B.

  • Câu 26: Thông hiểu

    Với giá trị nào của x thì mệnh đề chứa biến "\sqrt{x^{2}-3x+5}>2x+3" là đúng?

     Thay x=-1 vào 2 vế, ta được: 3>1 (đúng).

  • Câu 27: Vận dụng

    Phát biểu nào sau đây là mệnh đề đúng:

    Mệnh đề P \Rightarrow Q chỉ sai khi P đúng, Q sai.

    2.5 = 10là mệnh đề đúng, Luân Đôn là thủ đô của Hà Lan là mệnh đề sai \Rightarrow “2.5 = 10 \Rightarrow Luân Đôn là thủ đô của Hà Lan” là mệnh đề sai.

    7 là số lẻ là mệnh đề đúng,7 chia hết cho 2 là mệnh đề sai \Rightarrow “7 là số lẻ \Rightarrow 7 chia hết cho 2” là mệnh đề sai.

    81 là số chính phương là mệnh đề đúng, \sqrt{81} là số nguyên là mệnh đề đúng \Rightarrow “81 là số chính phương \Rightarrow \sqrt{81} là số nguyên” là mệnh đề đúng.

    Số 141 chia hết cho 3 là mệnh đề đúng, 141 chia hết cho 9 là mệnh đề sai \Rightarrow “Số 141 chia hết cho 3 \Rightarrow 141 chia hết cho 9” là mệnh đề sai.

    Chọn đáp án 81 là số chính phương \Rightarrow \sqrt{81} là số nguyên.

  • Câu 28: Nhận biết

    Cho A = {1; 3; 4; 7} và B = {3; 5; 7; 10} . Tập A\ B là:

     Ta có: A\ B = {1; 4}.

  • Câu 29: Thông hiểu

    Tìm mệnh đề phủ định của mệnh đề P:\sqrt{2} \leq 2.

    Mệnh đề phủ định là: \overline{P}:\sqrt{2} > 2.

  • Câu 30: Thông hiểu

    Cho mệnh đề P: “∀ x ∈ R: |x| ≥ 0” . Phủ định của mệnh đề P là:

     Phủ định của mệnh đề P là: “∃ x ∈ R: |x| < 0”.

  • Câu 31: Thông hiểu

    Tập hợp C = (2;+∞) \ [-3;8] bằng tập hợp nào sau đây?

     Ta có: C = (2;+∞) \ [-3;8] = (8;+∞).

  • Câu 32: Nhận biết

    Điền vào chỗ trống: “Hiệu của tập hợp A và tập hợp B là ….”

    Hiệu của tập hợp A và tập hợp B là tập hợp các phần tử thuộc A nhưng không thuộc B.

  • Câu 33: Nhận biết

    Tìm mệnh đề đúng.

    Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1,\ 3 là số lẻ.

    Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: 2.3 = 6 là số chẵn nhưng 3 là số lẻ.

    Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. là mệnh đề sai: Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1,3 là số lẻ.

    Chọn Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

  • Câu 34: Nhận biết

    Tìm đáp án không phải mệnh đề trong các câu sau.

    Câu “Bộ phim quá hay!” là câu cảm thán nên không phải là mệnh đề.

  • Câu 35: Nhận biết

    Có bao nhiêu câu là mệnh đề trong các câu sau:

    (1) Chăm chỉ lên nhé!

    (2) Số 20 chia hết cho 6.

    (3) Số 7 là số nguyên tố.

    (4) Số 3 là một số chẵn.

    Câu (1) là câu cảm thán nên không phải mệnh đề.

    Các câu còn lại là mệnh đề.

    \Rightarrow Có 3 câu là mệnh đề.

  • Câu 36: Thông hiểu

    Cho A = \left\{ x\mathbb{\in R}:x^{2} - 7x + 6 = 0 ight\} và B = \left\{ x\mathbb{\in R}:|x| < 4 ight\}. Khi đó:

    x^{2} - 7x + 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 6 \\ \end{matrix} ight.\ \Rightarrow A = \left\{ 1;6 ight\}.

    |x| < 4 \Rightarrow - 4 < x < 4 \Rightarrow B = ( - 4;4).

    Ta có: A\backslash B = \left\{ 6 ight\} \subset A.

  • Câu 37: Thông hiểu

    Xác định tập hợp B=\{x∈Z|−2≤x<3\} bằng cách liệt kê các phần tử.

     Ta có: B=\{x∈Z|−2≤x<3\} =\{–2; –1; 0; 1; 2\}.

  • Câu 38: Thông hiểu

    Cho mệnh đề chứa biến P(n):``n^{2} - 1 chia hết cho 4” với n là số nguyên. Xét xem các mệnh đề P(5) và P(2) đúng hay sai?

    Thay n = 5 và n = 2 vào P(n) ta được các số 24 \vdots 4 và 3 không chia hết cho 4. Vậy P(5) đúng và P(2) sai.

  • Câu 39: Thông hiểu

    Hai mệnh đề sau là mệnh đề gì: “x chia hết cho 9” và “x chia hết cho 3”.

     Nếu x chia hết cho 9 thì x chia hết cho 3.

    Nếu x chia hết cho 3 thì x có thể không chia hết cho 9.

    => Hai mệnh đề “x chia hết cho 9” và “x chia hết cho 3” là mệnh đề kéo theo.

  • Câu 40: Vận dụng

    Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = \lbrack - 4;4brack \cup \lbrack 7;9brack \cup \lbrack 1;7).

    Vậy A = \lbrack - 4;4brack \cup \lbrack 7;9brack \cup \lbrack 1;7) = \lbrack - 4;9brack.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Đại số 10 Chương 1 Kết nối tri thức Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 39 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Đại số 10 Chương 1 Kết nối tri thức
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập