Lớp 10 Toán 10 - Kết nối tri thức

Đề kiểm tra 45 phút Đại số 10 Chương 5 Kết nối tri thức

Mô tả thêm: Đề kiểm tra 1 tiết Toán 10 Các số đặc trưng của mẫu số liệu không ghép nhóm gồm 40 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Kết nối tri thức.
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Cho biểu đồ lượng mưa trung bình các tháng năm 2019 tại Thành phố Hồ Chí Minh như sau:

    Mẫu số liệu nhận được từ biểu đồ trên có khoảng biến thiên là:

    Quan sát biểu đồ ta thấy:

    Giá trị lớn nhất là 342

    Giá trị nhỏ nhất là: 4

    Vậy khoảng biến thiên của mẫu số liệu là: 342 – 4 = 338.

  • Câu 2: Thông hiểu

    Số gần đúng của a = 2,57656 có ba chữ số đáng tin viết dưới dạng chuẩn là:

    Vì số gần đúng của số a có ba chữ số đáng tin nên ba chữ số đó là 2,5,7.

    Nên cách viết dưới dạng chuẩn là 2,57.

  • Câu 3: Vận dụng

    Bảng dưới đây thể hiện sản lượng lúa (đơn vị: tạ) của một số thửa ruộng:

    Tính phương sai của mẫu số liệu.

    Số trung bình của mẫu là:

    \overline{x} =\frac{1.4 + 3.4,5 + 4.5 + 1.5,5 + 1.6}{1 + 3 + 4 + 1 + 1} = 4,9.

    Phương sai:

    s^{2} = \frac{(4 - 4,9)^{2} + 3.(4,5 - 4,9)^{2} + 4(5 - 4,9)^{2} + (5,5 - 4,9)^{2} + (6 - 4,9)^{2}}{10} = 0,29.

  • Câu 4: Nhận biết

    Số liệu xuất hiện nhiều nhất trong mẫu số liệu được gọi là:

    Số liệu xuất hiện nhiều nhất trong mẫu số liệu được gọi là mốt.

  • Câu 5: Thông hiểu

    Cho số a = 6653964 \pm 300. Số quy tròn của số gần đúng 6653964 là:

    Do độ chính xác d = 300 < \frac{1000}{2} nên làm quy tròn số gần đúng 6653964 đến hàng nghìn ta được: 6654000

  • Câu 6: Nhận biết

    Cho mẫu số liệu: 10; 8; 6; 2; 4. Tính phương sai của mẫu.

    Số trung bình là \overline{x} = \frac{10 + 8 + 6 + 2 + 4}{5} = 6.

    Phương sai là s^{2} = \frac{(10 - 6)^{2} + (8 - 6)^{2} + (6 - 6)^{2} + (2 - 6)^{2} + (4 - 6)^{2}}{5} = 8.

  • Câu 7: Nhận biết

    Cho số gần đúng a = 32567 với độ chính xác d = 300. Số quy tròn của số a là:

    Độ chính xác đến hàng trăm nên ta quy tròn đến hàng nghìn, ta được số quy tròn là 33000.

  • Câu 8: Nhận biết

    Số đặc trưng nào sau đây đo độ phân tán của mẫu số liệu?

    Số đặc trưng đo độ đo phân tán của mẫu số liệu là phương sai.

  • Câu 9: Nhận biết

    Cho một mẫu dữ liệu đã được sắp xếp theo thứ tự không giảm x_1 ≤ x_2 ≤ x_3 ≤ ... ≤ x_n. Khi đó khoảng biến thiên R của mẫu số liệu bằng:

    Khoảng biến thiên của mẫu số liệu bằng: R = x_n – x_1

  • Câu 10: Vận dụng

    Dưới đây là bảng thống kê số lần làm bài tập Toán của học sinh lớp 10A.

    Tìm trung vị của mẫu số liệu này.

    Cỡ mẫu số liệu này là: 2 + 4 + 6 + 12 + 8 + 3 = 35.

    Suy ra giá trị chính giữa là giá trị ở vị trí thứ 18. Đó là số 3.

    Vậy trung vị M_{e} = 3.

  • Câu 11: Thông hiểu

    Tính sản lượng lúa trung bình trong bảng thống kê dưới đây:

    Sản lượng (tạ)

    20

    21

    22

    23

    24

    Tần số

    5

    8

    11

    10

    6

    Sản lượng lúa trung bình là:

    \overline{x} = \frac{5.20 + 8.21 + 11.22 + 10.23 + 6.24}{40} = 22,1

    Vậy sản lượng lúa trung bình là 22,1 tạ.

  • Câu 12: Vận dụng

    Bạn An đo chiều dài của một sân bóng ghi được 250 \pm 0,2m. Bạn Bằng đo chiều cao của một cột cờ được 15 \pm 0,1m. Trong 2 bạn An và Bằng, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?

    Phép đo của bạn A có sai số tương đối \delta_{1} \leq \frac{0,2}{250} = 0,0008 = 0,08\%

    Phép đo của bạn B có sai số tương đối \delta_{2} \leq \frac{0,1}{15} = 0,0066 = 0,66\%

    Như vậy phép đo của bạn A có độ chính xác cao hơn.

  • Câu 13: Nhận biết

    Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, lớp trưởng thu được kết quả như sau:

    Số cuốn sách

    3

    4

    5

    6

    7

    Số học sinh

    6

    15

    3

    8

    8

    Tìm mốt của mẫu số liệu đã cho?

    Mốt của mẫu số liệu là 4 (vì có tần số lớn nhất).

  • Câu 14: Nhận biết

    Số cam có trong các giỏ được ghi lại như sau: 2;8;12;16. Số trung vị của mẫu số liệu là:

    Vì cỡ mẫu N = 4 là số chẵn nên trung vị bằng trung bình cộng của số liệu ở vị trí thứ hai và thứ ba.

    => Số trung vị của mẫu số liệu: \frac{8 + 12}{2} = 10

  • Câu 15: Vận dụng

    Nhà sản xuất công bố chiều dài và chiều rộng của 1 tấm ván hình chữ nhật lần lượt là 100 \pm 0,5 và 70 \pm 0,5 (đơn vị: cm). Tính diện tích của tấm thép.

    Gọi \overline{a} và \overline{b} lần lượt là chiều dài và chiều rộng thực của tấm thép.

    Ta có: 99,5 \leq \overline{a} \leq 100,5 và 69,5 \leq \overline{b} \leq 70,5.

    Suy ra: 99,5.69,5 = 6915,25 \leq \overline{a}.\overline{b} \leq 100,5.70,5 = 7085,25.

    Do đó: 6915,25 - 7000 = - 84,75 \leq \overline{a}.\overline{b} - 7000 \leq 7085,25 - 7000 = 85,25

    Vậy diện tích tấm thép là 7000 \pm 85,25.

  • Câu 16: Nhận biết

    Số quy tròn số 2,718282 với độ chính xác d = 0,01 là:

    Theo bài ra ta có: Độ chính xác 0,001 < d = 0,01 nên ta quy tròn số đến số thập phân thứ nhất.

    Vậy số quy tròn là 2,7.

  • Câu 17: Nhận biết

    Để điều tra các con trong mỗi gia đình của một chung cư gồm 100 gia đình. Người ta chọn ra 20 gia đình ở tầng 4 và thu được mẫu số liệu sau đây:

    2  4  2  1  3  5  1  1  2  3  1  2  2  3  4  1  1  2  3  4.

    Số trung bình cộng \bar{x} của mẫu số liệu trên là:

    Số trung bình cộng của mẫu số liệu trên là:

    \overline x = \frac{{1.6 + 2.6 + 3.4 + 4.3 + 5}}{{20}} = 2,35

  • Câu 18: Thông hiểu

    Điểm kiểm tra môn Văn của 2 tổ học sinh được thống kê:

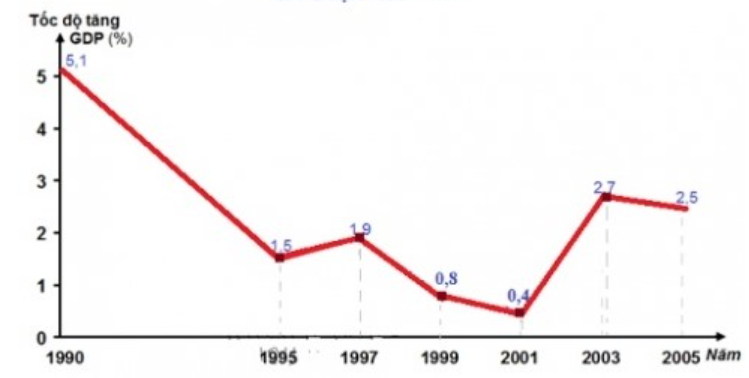
    Dựa vào khoảng biến thiên thì tổ nào học đều hơn?

    Khoảng biến thiên điểm của tổ 1 là R_{1} = 9 - 7 = 2.

    Khoảng biến thiên điểm của bạn Bình là R_{2} = 10 - 6 = 4.

    Vì R_{1} < R_{2} nên tổ 1 học đều hơn.

  • Câu 19: Nhận biết

    Quy tròn số 2,663 đến hàng phần chục ta được số 2,7. Sai số tuyệt đối là:

    Sai số tuyệt đối là: d = |2,7 - 2,663| = 0,037.

  • Câu 20: Thông hiểu

    Cho bảng điểm kiểm tra môn Toán của học sinh lớp 10B như sau:

    Điểm

    4

    5

    6

    7

    8

    9

    10

    Tổng

    Số học sinh

    2

    8

    7

    10

    8

    3

    2

    N = 40

    Tính số trung bình của mẫu số liệu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).

    Số trung bình của mẫu số liệu là:

    \overline{x} = \frac{2.4 + 5.8 + 6.7 + 7.10 + 8.8 + 9.3 + 10.2}{40} \approx 6,8

    Vậy số trung bình của mẫu số liệu bằng 6,8.

  • Câu 21: Nhận biết

    Phương sai của một mẫu số liệu \left \{ x_1;x_2;...;x_N ight \} bằng

     Phương sai của một mẫu số liệu \left \{ x_1;x_2;...;x_N ight \} bằng bình phương của độ lệch chuẩn.

  • Câu 22: Vận dụng

    Hình dưới thống kê tỉ lệ phần trăm thất nghiệp ở một số quốc gia:

    Hãy tìm giá trị bất thường (nếu có) của mẫu số liệu.

    Sắp xếp các giá trị theo thứ tự không giảm:

    3,2 3,6 4,4 4,5 5,0 5,4 6,0 6,7 7,0 7,2 7,7 7,8 8,4 8,6 8,7

    Từ mẫu số liệu ta tính được: Q_{2} = 6,7 và Q_{1} = 4,5, Q_{3} = 7,8.

    Suy ra \Delta_{Q} = Q_{3} - Q_{1} = 7,8 - 4,5 = 3,3.

    Ta có: Q_{1} - 1,5\Delta_{Q} = 4,5 - 1,5.3,3 = - 0,45.

    Ta có: Q_{3} + 1,5\Delta_{Q} = 7,8 + 1,5.3,3 = 12,75.

    Ta thấy không có số liệu nào nhỏ hơn - 0,45 và lớn hơn 12,75 nên mẫu không có giá trị bất thường.

  • Câu 23: Nhận biết

    Điểm kiểm tra của 24 học sinh được ghi lại trong bảng sau:

    Mốt của mẫu số liệu là:

    Điểm 8 có tần số xuất hiện nhiều nhất nên mốt của mẫu số liệu là 8.

  • Câu 24: Nhận biết

    Cho bảng số liệu số máy tính bán được trong quý I đầu năm 2022 của một cửa hàng:

    Hãng

    HP

    Lenovo

    Asus

    Apple

    Dell

    Razer

    Số máy tính bán được

    55

    45

    42

    36

    60

    15

    Mốt của bảng số liệu trên là hãng máy tính nào?

    Số máy tính bán được nhiều nhất là 60 máy thuộc hãng Dell

    => Mốt của bảng số liệu trên là hãng Dell.

  • Câu 25: Vận dụng

    Dưới đây là bảng thống kê số lần làm bài tập Toán của học sinh lớp 10A.

    Tìm tứ phân vị của mẫu số liệu này.

    Cỡ mẫu số liệu này là: 2 + 4 + 6 + 12 + 8 + 3 = 35.

    Suy ra giá trị chính giữa là giá trị ở vị trí thứ 18. Đó là số 3. Suy ra trung vị M_{e} = 3 = Q_{2}.

    Trung vị của 17 giá trị bên trái Q_{2} là giá trị ở vị trí thứ 9. Đó là số 2. Suy ra Q_{1} = 2.

    Trung vị của 17 giá trị bên phải Q_{2} là giá trị ở vị trí thứ 27. Đó là số 4. Suy ra Q_{3} = 4.

  • Câu 26: Thông hiểu

    Dự báo thời tiết trong 10 ngày tại tỉnh A được ghi lại trong bảng sau:

    Ngày

    22

    23

    24

    25

    26

    27

    28

    29

    30

    31

    Nhiệt độ (0C)

    24

    25

    26

    27

    27

    26

    27

    21

    19

    18

    Tìm phương sai của mẫu số liệu đã cho?

    Ta có: N = 10

    Nhiệt độ trung bình của 10 ngày là:

    \overline{x} = \frac{24 + 25 + 26 + 27 + 28 + 26 + 27 + 21 + 19 + 18}{10} = 24

    Phương sai của mẫu số liệu là:

    s^{2} = \frac{1}{10}\lbrack(24 - 24)^{2} + (25 - 24)^{2} + (26 - 24)^{2}

    + (27 - 24)^{2} + (28 - 24)^{2} + (26 - 24)^{2} + (27 - 24)^{2}

    + (21 - 24)^{2} + (19 - 24)^{2} + (18 - 24)^{2}brack = 10,6

    Vậy phương sai cần tìm là 10,6.

  • Câu 27: Thông hiểu

    Quy tròn số 54 739 đến hàng trăm và ước lượng sai số tương đối.

    Quy tròn số 54 739 đến hàng trăm ta được số gần đúng là a = 54{\text{ 700}}

    Ta có:

    {\Delta _a} = \left| {\overline a - a} ight| = \left| {54739 - 54{\text{ 700}}} ight| = 39 < 40

    => {\delta _a} = \frac{{{\Delta _a}}}{{\left| a ight|}} = \frac{{40}}{{54700}} \approx 0,073\%

  • Câu 28: Thông hiểu

    Cho bảng tần số như sau:

    Giá trị

    x1

    x2

    x3

    x4

    x5

    x6

    Tần số

    15

    9n - 1

    12

    n^{2} + 7

    10

    17

    Tìm n để M_{0}^{(1)}=x_2;M_{0}^{(2)}=x_4 là hai mốt của bảng tần số trên.

    Ta có: 

    M_{0}^{(1)}=x_2;M_{0}^{(2)}=x_4

    \begin{matrix} \Rightarrow 9n - 1 = {n^2} + 7,\left( {n > 2} ight) \hfill \\ \Leftrightarrow {n^2} - 9n + 8 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {n = 1\left( {ktm} ight)} \\ {n = 8\left( {tm} ight)} \end{array}} ight. \hfill \\ \end{matrix}

    Vậy n = 8.

     

  • Câu 29: Nhận biết

    Kết quả thống kê số tiền điện của một hộ gia đình trong 6 tháng liên tiếp (đơn vị: nghìn đồng) như sau: 270;\ 300;\ 350;\ 320;\ 310;\ 280. Khoảng biến thiên của mẫu số liệu bằng:

    Giá trị lớn nhất bằng 350

    Giá trị nhỏ nhất bằng 270

    => Khoảng biến thiên của mẫu số liệu là: 350 – 270 = 80.

    Vậy khoảng biến thiên của mẫu số liệu bằng 80.

  • Câu 30: Nhận biết

    Làm tròn số 5,2463 đến hàng phần trăm ta được kết quả là:

    Làm tròn số 5,2463 đến hàng phần trăm ta được kết quả là 5,25.

  • Câu 31: Nhận biết

    Khẳng định nào sau đây là đúng?

     Khẳng định đúng là: "Nếu sai số tương đối của phép đo càng nhỏ thì chất lượng phép đo càng cao."

  • Câu 32: Thông hiểu

    Tìm phương sai của dãy số liệu: 8 15 14 18.

    Số trung bình của mẫu số liệu là: \overline{x} = \frac{8 + 15 + 14 + 18}{4} = 13.

    Ta có phương sai: s^{2} = \frac{(8 - 13)^{2} + (15 - 13)^{2} + (14 - 13)^{2} + (18 - 13)^{2}}{4} = 13,75.

  • Câu 33: Thông hiểu

    Số quy tròn của 45,6534 với độ chính xác d = 0,01 là:

    Xét d = 0,01 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần trăm.

    Nên suy ra hàng lớn nhất có độ chính xác d = 0,01 là hàng phần trăm nên ta quy tròn số 45,6534 ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần mười.

    Xét chữ số ở hàng phần trăm của 45,6534 là 5 nên ta suy ra được số quy tròn của 45,6534 đến hàng phần mười là 45,7.

  • Câu 34: Nhận biết

    Quy tròn số 14869 đến hàng trăm. Số gần đúng nhận được là:

     Quy tròn 14869 đến hàng trăm, ta được: 14900.

  • Câu 35: Thông hiểu

    Cho mẫu số liệu: 10 7 8 5 4. Tính độ lệch chuẩn của mẫu số liệu đó.

     Số trung bình: \overline x = \frac{{10 + 7 + 8 + 5 + 4}}{5} = 6,8.

    Phương sai: {s^2} =\frac{{{{(10 - 6,8)}^2} + {{(7 - 6,8)}^2} + ... + {{(4 - 6,8)}^2}}}{2}= 4,56.

    Độ lệch chuẩn: \sqrt {{s^2}} \approx 2,14.

  • Câu 36: Nhận biết

    Viết số quy tròn của số 3546790 đến hàng trăm.

    Quy tròn số đến hàng trăm nên chữ số quy tròn là chữ số, mà chữ số sau chữ số 7 là 9 > 5 nên số quy tròn của số 3546790 đến hàng trăm là 3546800.

  • Câu 37: Nhận biết

    Cho mẫu số liệu như sau:

    Khoảng biến thiên của mẫu số liệu trên là:

    Quan sát mẫu số liệu ta thấy:

    Giá trị lớn nhất là 29.

    Giá trị nhỏ nhất là 23

    Suy ra khoảng biến thiên của mẫu số liệu là: 29 – 23 = 6.

    Vậy đáp án là 6.

  • Câu 38: Thông hiểu

    Một túi gạo có ghi thông tin khối lượng là 5 \pm 0,2kg. Khi đó khối lượng thực của bao gạo nằm trong đoạn nào sau đây?

    Khi một túi gạo có ghi thông tin khối lượng là 5 \pm 0,2kg thì khối lượng thực của bao gạo nằm trong đoạn \lbrack 4,8;5,2brack.

  • Câu 39: Nhận biết

    Cho dãy số liệu 1;1;2;3;4;4;5;5;5;6. Xác định mốt của mẫu số liệu?

    Mốt số liệu đã cho có số 5 xuất hiện nhiều lần nhất

    Suy ra mốt của mẫu số liệu là 5.

  • Câu 40: Thông hiểu

    Cho \overline{a} = \frac{16}{7} = 2,285714... Hãy xác định số gần đúng a của \overline{a} với độ chính xác d = 0,03.

    Ta có hàng của chữ số 0 đầu tiên bên trái của d là hàng phần trăm. Ta cần quy tròn đến hàng phần trăm được số gần đúng là a = 2,29.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Đại số 10 Chương 5 Kết nối tri thức Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 19 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Đại số 10 Chương 5 Kết nối tri thức
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập