Đồ thị hàm số y = sinx được suy ra từ đồ thị C của hàm số y = cosx bằng cách.
Ta có:
=> Đồ thị hàm số y = sinx được suy ra từ đồ thị C của hàm số y = cosx bằng cách tịnh tiến C qua phải một đoạn có độ dài là
Đồ thị hàm số y = sinx được suy ra từ đồ thị C của hàm số y = cosx bằng cách.
Ta có:
=> Đồ thị hàm số y = sinx được suy ra từ đồ thị C của hàm số y = cosx bằng cách tịnh tiến C qua phải một đoạn có độ dài là
Một đồng hồ treo tường, kim giờ dài 10,57cm và kim phút dài 13,34cm. Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là
Ta có: 6 giờ thì kim giờ vạch lên 1 cung có số đo
=> 30 phút kim giờ vạch lên 1 cung có số đo là
=> Độ dài cung tròn mà nó vạch lên là
Tất cả các nghiệm của phương trình tan (x) = cot (x) là?
Điều kiện
thỏa mãn điều kiện.
Tính giá trị đúng của biểu thức ![]()
Ta có:
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình ![]() có nghiệm?
có nghiệm?
Ta có .
Phương trình có nghiệm
Vậy có tất cả 3 giá trị nguyên của tham số m.
Cho góc ![]() thỏa mãn
thỏa mãn ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]()
Ta có:
Theo bài ra ta có:
Khi đó giá trị biểu thức T là:
Biến đổi thành tích biểu thức ![]() ta được
ta được
Ta có
Phương án nào sau đây sai với mọi ![]() ?
?
Ta có:
Vậy đáp án sai là:
Tìm tập xác định ![]() của hàm số
của hàm số ![]() ?
?
Ta có:
Hàm số được xác định khi
Vậy tập xác định của hàm số là
Gọi T là tập giá trị của hàm số ![]() . Tìm tổng các giá trị nguyên của T.
. Tìm tổng các giá trị nguyên của T.
Ta có:
Vì
Do đó tổng các giá trị nguyên của T là 7.
Tìm tập xác định D của hàm số ![]()
Hàm số xác định khi và chỉ khi
Vậy tập xác định của hàm số là
Chọn công thức đúng trong các công thức cho sau đây?
Công thức đúng là:
Cho tam giác ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Ta có:
Do đó
Vậy khẳng định sai là:
Tập xác định của hàm số: ![]()
Ta có:
Điều kiện xác định của hàm số ![]() là:
là:
Ta có:
Điều kiện xác định của hàm số
Với ![]() là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
Đẳng thức đúng: .
Giải phương trình ![]() .
.
Ta có .
Với
Với
Nhận thấy chưa có đáp án nào phù hợp. Ta biểu diễn các nghiệm trên đường tròn lượng giác (hình vẽ).
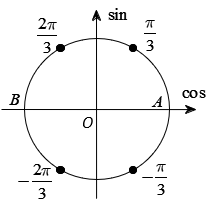
Nếu tính luôn hai điểm A, B thì có tất cả 6 điểm cách đều nhau nên ta gộp được 6 điểm này thành một họ nghiệm, đó là .
Suy ra nghiệm của phương trình
Điều kiện để phương trình ![]() có nghiệm là:
có nghiệm là:
Điều kiện để phương trình có nghiệm là
Vậy thì phương trình đã cho có nghiệm.
Nghiệm của phương trình 2cos (2x) =-2
Ta có:
.
Với điều kiện xác định của các giá trị lượng giác, cho ![]() . Đơn giản biểu thức P ta được:
. Đơn giản biểu thức P ta được:
Ta có:
Giá trị nào sau đây của x thỏa mãn ![]() ?
?
Ta có:
Tập nghiệm của phương trình ![]() là:
là:
Ta có:
Tìm chu kì của hàm số ![]() ?
?
Hàm số tuần hoàn với chu kì
Áp dụng công thức trên ta suy ra hàm số tuần hoàn với chu kì
.
Hàm số ![]() nghịch biến trên khoảng nào sau đây?
nghịch biến trên khoảng nào sau đây?
Hàm số tuần hoàn với chu kì
Do hàm số nghịch biến trên
=> Hàm số nghịch biến khi
Vậy đáp án đúng là
Cho vòng tròn lượng giác được kí hiệu như sau:

Điểm nào biểu diễn nghiệm của phương trình ![]() ?
?
Ta có:
Vậy chỉ có hai điểm C và điểm D thỏa mãn yêu cầu bài toán.
Cho ![]() cho
cho ![]() . Tính giá trị của
. Tính giá trị của ![]() ?
?
Ta có:
Vì nên
Trên đường tròn lượng giác, cung có số đo ![]() được biểu diễn bởi bao nhiêu điểm?
được biểu diễn bởi bao nhiêu điểm?
Xét theo chiều dương với ta thấy cung có số đo
được biểu diễn bởi ba điểm trên đường tròn lượng giác như sau:
Nếu ![]() và
và ![]() là hai nghiệm của phương trình
là hai nghiệm của phương trình ![]() thì
thì ![]() bằng:
bằng:
Ta có: và
là hai nghiệm của phương trình
nên theo định lí Vi – ét ta có:
Khi đó:
Tổng các nghiệm của phương trình ![]() trong khoảng
trong khoảng ![]() là:
là:
Giải phương trình:
Xét nghiệm
Do =>
=>
Xét nghiệm
Do
vậy tổng tất cả các nghiệm của phương trình là:
Cho góc ![]() được biểu diễn trên đường tròn lượng giác như hình vẽ. Mệnh đề nào dưới đây đúng?
được biểu diễn trên đường tròn lượng giác như hình vẽ. Mệnh đề nào dưới đây đúng?

Góc được biểu diễn như hình vẽ, khi đó
.
Tung độ của điểm là
suy ra
Mệnh đề đúng là .
Giá trị lớn nhất của hàm số ![]() tại điểm là nghiệm của phương trình nào dưới đây?
tại điểm là nghiệm của phương trình nào dưới đây?
Theo bài ra ta có:
Phương trình (*) có nghiệm
Vậy giá trị lớn nhất của hàm số bằng 1 lúc đó
Tính giá trị biểu thức ![]()
Ta có:
Tập nghiệm của phương trình ![]() là?
là?
Cho tam giác ![]() có các góc
có các góc ![]() bất kì. Biểu thức
bất kì. Biểu thức ![]() không thể nhận giá trị nào sau đây?
không thể nhận giá trị nào sau đây?
Ta có:
Với tam giác ABC bất kì ta luôn có:
Vậy biểu thức không thể nhận giá trị
.
Có bao nhiêu giá trị nguyên của m để phương trình ![]() có nghiệm?
có nghiệm?
Ta có:
Kết hợp với m thuộc tập số nguyên
Suy ra 4 – (-2) + 1 = 7 giá trị nguyên của m
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức ![]() .
.
Ta có:
Theo bài ra ta có:
=>
Phương trình ![]() có nghiệm là:
có nghiệm là:
Xét đường tròn lượng giác như hình vẽ. Biết ![]() , E và D lần lượt là các điểm đối xứng của C và F qua gốc O. Nghiệm của phương trình
, E và D lần lượt là các điểm đối xứng của C và F qua gốc O. Nghiệm của phương trình ![]() được biểu diễn trên đường tròn lượng giác là những điểm nào?
được biểu diễn trên đường tròn lượng giác là những điểm nào?
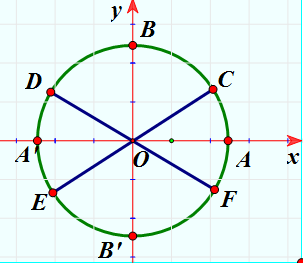
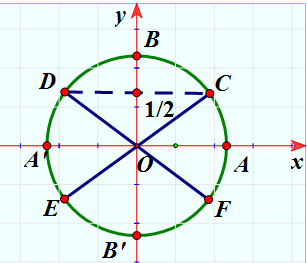
Ta có:
Dựa vào đường tròn lượng giác ta có điểm biểu diễn nghiệm của phương trình là điểm C và điểm D.
Gọi ![]() là nghiệm âm lớn nhất của
là nghiệm âm lớn nhất của ![]() . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?
Phương trình
So sánh hai nghiệm ta được nghiệm âm lớn nhất của phương trình là
Trong các hàm số sau, hàm số nào là hàm số chẵn?
Xét hàm số có:
Tập xác định
Khi đó với ta có:
Vậy hàm số y = sinx là hàm số lẻ
Xét hàm số có:
Tập xác định
Khi đó với ta có:
Vậy hàm số y = x.cosx là hàm số lẻ
Xét hàm số có:
Tập xác định
Khi đó với ta có:
Vậy hàm số là hàm số lẻ
Xét hàm số có:
Tập xác định
Khi đó với ta có:
Vậy hàm số là hàm số chẵn
