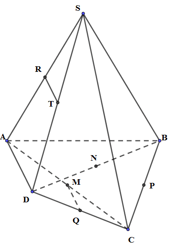
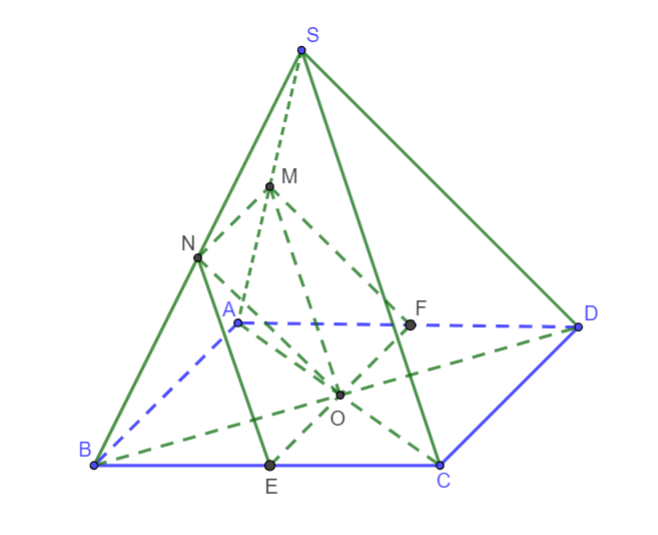
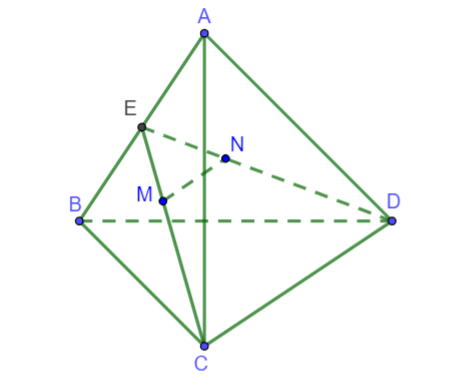
Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành. Gọi
là hình bình hành. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Gọi
. Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Tính tỉ số
. Tính tỉ số ![]() .
.
Đáp án: 1
Cho hình chóp có đáy
là hình bình hành. Gọi
lần lượt là trung điểm của
và
. Gọi
là trung điểm của
. Gọi
là giao điểm của
và
. Tính tỉ số
.
Đáp án: 1
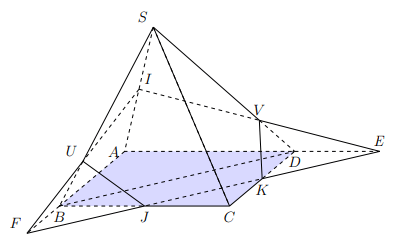
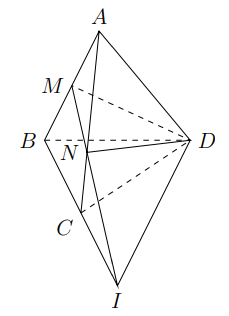
Hình vẽ minh họa
-Ta có .
Trong mặt phẳng , gọi
Suy ra .
Ta có:
-Trong mp , gọi
.
Ta có .