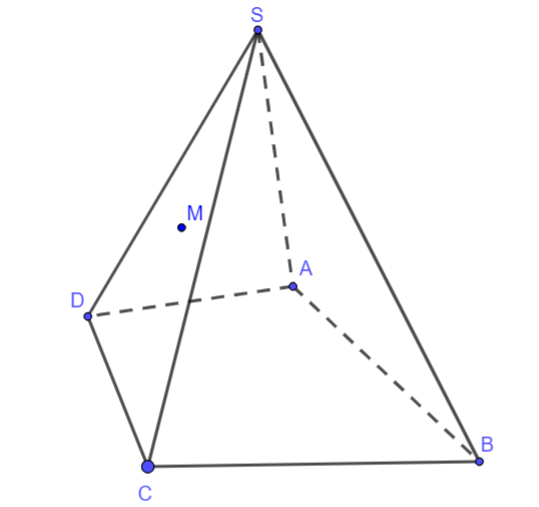
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?
Hình vẽ minh họa
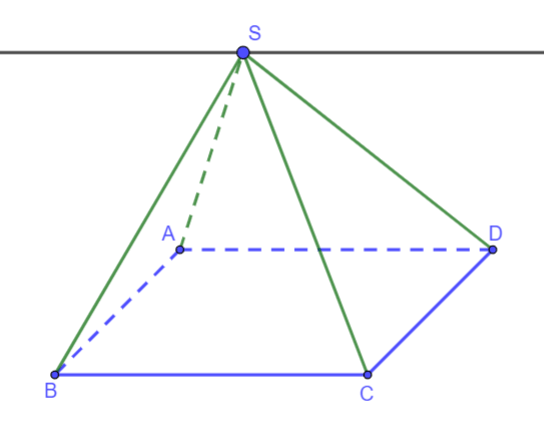
Xét (SAD) và (SBC) có:
S là điểm chung
=> Giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD