Cho khối chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh bằng
là hình vuông cạnh bằng ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() , biết
, biết ![]() .
.
Hình vẽ minh họa
Kẻ
Ta có:
Lại có:
Xét tam giác SAB vuông tại A có:
Cho khối chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh bằng
là hình vuông cạnh bằng ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() , biết
, biết ![]() .
.
Hình vẽ minh họa
Kẻ
Ta có:
Lại có:
Xét tam giác SAB vuông tại A có:
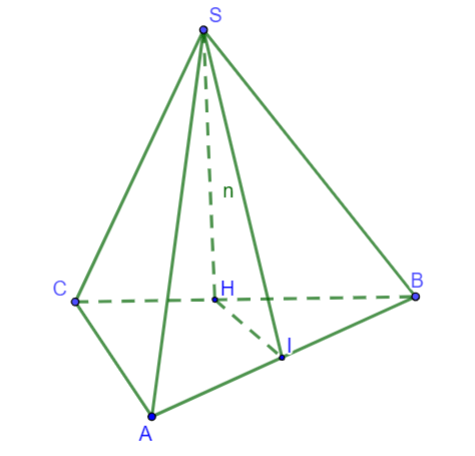
Cho tứ diện đều ![]() cạnh bằng
cạnh bằng ![]() ,
, ![]() là trung điểm của cạnh
là trung điểm của cạnh ![]() . Xác định góc giữa hai đường thẳng
. Xác định góc giữa hai đường thẳng ![]() và
và ![]() ?
?
Hình vẽ minh họa
Gọi N là trung điểm của AC thì MN // AB
Suy ra
Ta có:
Cho tứ diện ABCD với các đường thẳng AB, AC, AD đôi một vuông góc, H là trực tâm tam giác BCD. Góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc nào trong các góc sau đây?
Dễ thấy rằng BA⊥(ACD), AH⊥(BCD), suy ra góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc giữa hai đường thẳng BA và AH, tức là bằng góc
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; SAB là tam giác cân tại S; AD = 3BC = 3AB = 3a. Gọi M là điểm thuộc đoạn AD sao cho AD = 3MD. Biết rằng SCM là tam giác đều. Gọi α là góc giữa đường thẳng SB và mặt phẳng (SAD). Khi đó cos α nhận giá trị là
Gọi K là trung điểm AB, N là trung điểm của AM, H là trung điểm của CM.
Điểm M thuộc đoạn AD sao cho 3MD = AD = 3a
=> MD = a; AM = 2a
Tam giác SAB cân tại A nên AB ⊥ SK.
Vì HK là đường trung bình của hình thang vuông ABCM nên AB ⊥ HK và
Ta có: (1)
Tam giác SCM đều nên CM ⊥ SH (2)
Từ (1) và (2) suy ra SH ⊥ (ABCD)
Ta có AN = MN = MD = a nên ABCN là hình vuông, từ đó tam giác CMN vuông cân tại N.
Suy ra và
Tam giác SCM đều cạnh bằng nên
Tứ diện HSMN có HS, MN, HN đôi một vuông góc, đặt d = d(H, (SMN)).
Ta có:
Ta lại có:
Gọi I là hình chiếu của điểm B trên mặt phẳng (SAD)
Khi đó góc giữa đường thẳng SB và mặt phẳng (SAD) là góc
Do BC // AD => BC //(SAD)
=>
Trong tam giác vuông BIS ta có:
Cho tứ diện ABCD có AC = AD = BC = BD = a, (ACD) ⊥ (BCD) và (ABC) ⊥ (ABD). Tính độ dài cạnh CD.
Gọi M, N lần lượt là trung điểm của CD, AB, ∆ACD và ∆BCD cân
=> AM ⊥ CD, BM ⊥ CD. Ta có:
=> AM ⊥ BM
Và ta dễ dàng chứng minh được ∆ACD = ∆BCD (c – c - c)
=> AM = BM => ∆ABM vuông cân tại M
=> MN ⊥ AB
Đặt CD = x
Áp dụng định lý Py-ta-go ta có:
Xét ∆ABM vuông cân tại M
Áp dụng định lý Py-ta-go ta có:
Xét ∆CDN vuông cân tại N
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại ![]() , các cạnh
, các cạnh ![]() , các góc
, các góc ![]() . Gọi
. Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên
trên ![]() và
và ![]() . Tính cosin góc giữa hai mặt phẳng
. Tính cosin góc giữa hai mặt phẳng ![]() và
và ![]() .
.
Đáp án: 1/3 (Ghi đáp án dưới dạng phân số tối giản a/b).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , các cạnh
, các góc
. Gọi
là hình chiếu vuông góc của
trên
và
. Tính cosin góc giữa hai mặt phẳng
và
.
Đáp án: 1/3 (Ghi đáp án dưới dạng phân số tối giản a/b).
Hình vẽ minh họa
Gọi là mặt phẳng qua
và vuông góc với
.
Gọi là mặt phẳng qua
và vuông góc với
Khi đó, với
là đỉnh thứ tư của hình vuông ABHC.
Khi đó: là hai tam giác vuông bằng nhau có
.
Gọi là chân đường cao hạ từ đỉnh
của tam giác SAB, ta có
.
Vậy góc giữa hai mặt phẳng và
là
.
Xét cân tại
có
.
Ta có: .
Vậy cosin góc giữa hai mặt phẳng và
bằng
.
Cho hình chóp ![]() có đáy là tam giác vuông cân tại
có đáy là tam giác vuông cân tại ![]() . Tam giác
. Tam giác ![]() là tam giác đều cạnh
là tam giác đều cạnh ![]() và nằm trong mặt phẳng vuông góc với mặt đáy. Tính
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính ![]() ?
?
Hình vẽ minh họa
Gọi H là trung điểm của . Suy ra
Kẻ
Ta có:
Từ (1) và (2) suy ra HK là đoạn vuông góc chung của SA và BC
Do đó
Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Gọi I là hình chiếu của điểm O trên mặt phẳng (ABC). Điểm I là:
Ta có:
Chứng minh tương tự ta được:
Vậy I là trực tâm của tam giác ABC.
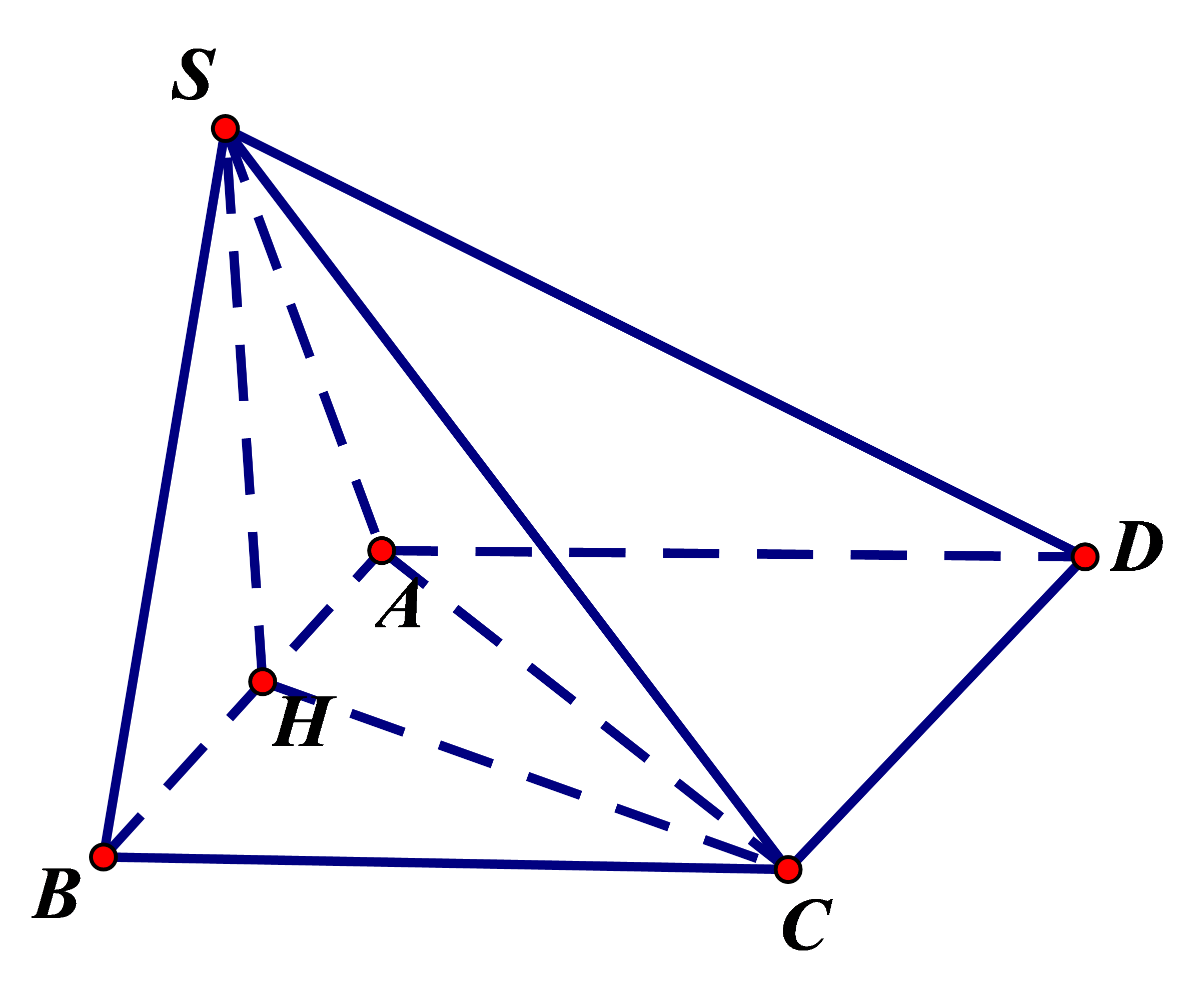
Cho hình chóp ![]() có đáy
có đáy ![]() là hình thang vuông tại hai đỉnh
là hình thang vuông tại hai đỉnh ![]() . Biết rằng
. Biết rằng ![]() ,
, ![]() . Chọn kết luận đúng dưới đây?
. Chọn kết luận đúng dưới đây?
Hình vẽ minh họa
Ta có: vuông cân tại C nên
mà
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Chiều cao của hình chóp bằng:
Hình vẽ minh họa:
Do S.ABCD là hình chóp tứ giác đều nên đáy ABCD là hình vuông và các cạnh bên bằng nhau.
Gọi O là hình chiếu của S trên mặt phẳng (ABCD).
Khi đó các tam giác SOA, SOB, SOC, SOD bằng nhau nên bốn đoạn thẳng OA, OB, OC, OD bằng nhau.
Suy ra O trùng với tâm của hình vuông ABCD, hay O là giao điểm của AC và BD. Vậy chiều cao của hình chóp là:
Cho tứ diện S.ABC có SBC và ABC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác SBC đều, tam giác ABC vuông tại A. Gọi H, I lần lượt là trung điểm của BC và AB. Khẳng định nào sau đây sai?
Hình vẽ minh họa:
Ta có: SBC là tam giác đều có H là trung điểm BC nên
Mà (SBC)⊥(ABC) theo giao tuyến BC
=> đúng.
Ta có HI là đường trung bình của ΔABC nên
=> đúng.
Ta có
=> đúng
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên ![]() và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
Hình vẽ minh họa:
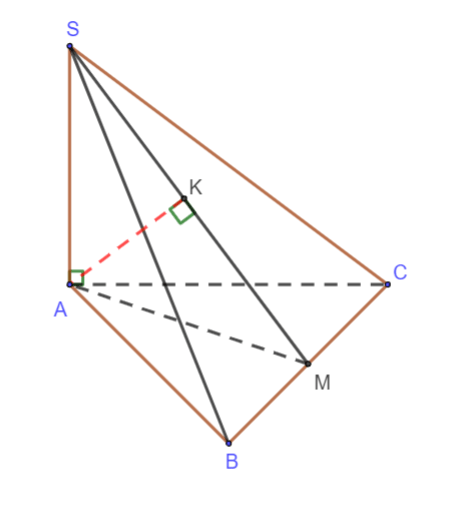
Gọi M là trung điểm BC
=>AM ⊥ BC và
Gọi K là hình chiếu của A trên SM => AK ⊥ SM (1)
Ta có:
Từ (1) và (2)
Xét tam giác SAM ta có:
Vậy
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2a, BC = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 600. Tính cosin góc giữa hai đường thẳng SB và AC.
+) Ta có:
+) Mặt khác
=>
Cho hình chóp ![]() có đáy là hình vuông
có đáy là hình vuông ![]() ;
; ![]() và
và ![]() . Gọi trung điểm của
. Gọi trung điểm của ![]() lần lượt là
lần lượt là ![]() . Tính số đo góc giữa đường thẳng
. Tính số đo góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() ?
?
Hình vẽ minh họa
Ta có:
là đường trung bình của tam giác
Ta lại có: nên AB là hình chiếu vuông góc của SB lên (SAD)
Mặt khác
Suy ra tam giác SAB vuông cân tại A
Các đường thẳng cùng vuông góc với một đường thẳng thì:
Đáp án "Thuộc một mặt phẳng" sai vì có thể xảy ra trường hợp nằm trên nhiều mặt phẳng khác nhau.
Đáp án "Vuông góc với nhau" sai vì có thể xảy ra trường hợp chúng song song với nhau.
Đáp án "Song song với nhau" sai vì có thể xảy ra trường hợp chúng cắt nhau.
Đáp án "Song song với một mặt phẳng" đúng vì chúng đồng phẳng.
Trong các mệnh đề sau, mệnh đề nào sai?
Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho trước.
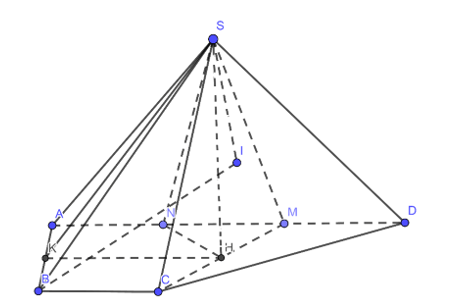
Cho tứ diện ![]() có các cạnh
có các cạnh ![]() đôi một vuông góc với nhau. Gọi trung điểm của các cạnh
đôi một vuông góc với nhau. Gọi trung điểm của các cạnh ![]() lần lượt là
lần lượt là ![]() . Tính thể tích tứ diện
. Tính thể tích tứ diện ![]() , biết
, biết ![]() .
.
Hình vẽ minh họa
Ta có:
Nhận thấy
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bằng a, chiều cao b. Biết góc giữa hai đường thẳng AC’ và A’B bằng 600. Tính b theo a.
Hình vẽ minh họa:
Lấy M, N, P, Q lần lượt là trung điểm của các cạnh AB, AA’, A’C’, A’B’ suy ra MN, NP, PQ và MQ lần lượt là đường trung bình của tam giác ABA’, AA’C’, A’B’C’ và hình chữ nhật ABB’A’. Suy ra:
Từ đó suy ra: tam giác MNP đều
=> MP = MN =
Kết hợp với
=> Tam giác MNP vuông tại Q
=>
=>
Cho hình chóp S.ABCD có đáy là hình bình hành và SA = SB = SC = 11, ![]() ,
, ![]() . Tính khoảng cách d giữa hai đường thẳng AB và SD?
. Tính khoảng cách d giữa hai đường thẳng AB và SD?
Hình vẽ minh họa:
Dựa vào định lý cosin ta dễ dàng tính được BC = 11,
=> ∆ABC vuông tại C
Do SA = SB = SC, nên hình chiếu của S xuống mặt phẳng (ABC) trùng với trung điểm H của AB
=> SH ⊥ (ABCD) và
Kẻ HK ⊥ CD, AP ⊥ CD, tứ giác APKH là hình chữ nhật, (Do
)
Trong tam giác vuông SHK, kẻ HI ⊥ SK
Do AB // CD => d(AB, SD) = d(H, SD) = HI
Ta có:
Cho hình lăng trụ tam giác ![]() có tất cả các cạnh bằng nhau. Hãy tính số đo góc giữa hai đường thẳng
có tất cả các cạnh bằng nhau. Hãy tính số đo góc giữa hai đường thẳng ![]() và
và ![]() ?
?
Hình vẽ minh họa
Ta có: Tam giác là tam giác đều suy ra
Lại có
.
Cho hai mặt phẳng (P), (Q) là hai mặt phẳng vuông góc với nhau có giao tuyến là đường thẳng m và a, b, c, d là các đường thẳng. Trong các khẳng định sau, khẳng định nào sai?
"Nếu b ⊥ m thì b ⊂ (P) hoặc b ⊂ (Q)" là khẳng định sai vì có thể b ⊂ (P) và b ⊂ (Q).
Cho khối chóp ![]() có chiều cao bằng
có chiều cao bằng ![]() đáy là tam giác
đáy là tam giác ![]() có diện tích bằng
có diện tích bằng ![]() . Thể tích khối chóp đã cho là:
. Thể tích khối chóp đã cho là:
Ta có:
Thể tích khối chóp tam giác là
Cho hình chóp S.ABCD có đáy là hình vuông ABCD, SA vuông góc với đáy. Kẻ AH vuông góc với SB (H ∈ SB). Chọn mệnh đề đúng.
Hình vẽ minh họa:
Ta có:
SA ⊥ BC
AB ⊥ BC
=> BC ⊥ (SAB) => BC ⊥ AH
Mà AH ⊥ SB nên AH ⊥ (SBC) => AH ⊥ SC
Cho hình chóp tam giác ![]() có
có ![]() và
và ![]() . Kết quả nào dưới đây đúng?
. Kết quả nào dưới đây đúng?
Ta có:
suy ra tam giác ABC vuông tại A
=> M là tâm đường tròn ngoại tiếp tam giác ABC.
Vì nên
là đường cao của hình chóp
.
Hình vẽ minh họa
Gọi N, I lần lượt là trung điểm cạnh AC và SB.
Ta có: MN // AB và IM // SC nên
Mà
Xét tam giác IMN có
Cho khối chóp tam giác đều ![]() có cạnh đáy bằng 1cm và các cạnh bên bằng 2cm. Khi đó thể tích khối chóp bằng bao nhiêu?
có cạnh đáy bằng 1cm và các cạnh bên bằng 2cm. Khi đó thể tích khối chóp bằng bao nhiêu?
Hình vẽ minh họa
Do đáy là tam giác đều nên gọi I là trung điểm của BC khi đó AI là đường cao của tam giác đáy.
Theo định lí Pythagore ta có:
Trong tam giác SOA vuông tại O ta có:
Vậy thể tích khối chóp tam giác là:
Cho tứ diện ABCD có độ dài các cạnh AB = a, AD = BC = b, AB là đoạn vuông góc chung của BC và AD và (AB, CD) = α, 00 < α < 900, tan α < ![]() . Gọi I là trung điểm AB, điểm M thuộc đoạn AB sao cho IM = x và (P) là mặt phẳng đi qua M vuông góc với AB đồng thời cắt CD tại N. Diện tích hình tròn tâm M bán kính MN bằng
. Gọi I là trung điểm AB, điểm M thuộc đoạn AB sao cho IM = x và (P) là mặt phẳng đi qua M vuông góc với AB đồng thời cắt CD tại N. Diện tích hình tròn tâm M bán kính MN bằng
Hình vẽ minh họa:
Dựng hình lăng trụ đứng tam giác ADE.BFC như hình vẽ, trong đó AB là cạnh bên.
Khi đó mặt phẳng (P) song song với hai mặt phẳng đáy của hình lăng trụ nói trên.
Gọi P, Q lần lượt là giao điểm của (P) với CE và DF.
Không mất tính tổng quát, giả sử M thuộc đoạn AI.
Ta có = (CD, DF) = (CD, AB) = α, suy ra PQ = CF = a tan α.
Do đó:
Vậy
Cho lăng trụ đều ABC.A’B’C’ có AB = 1; AA’ = m (m > 0). Để góc giữa AB’ và BC’ bằng 600 thì m có giá trị là bao nhiêu?
Hình vẽ minh họa
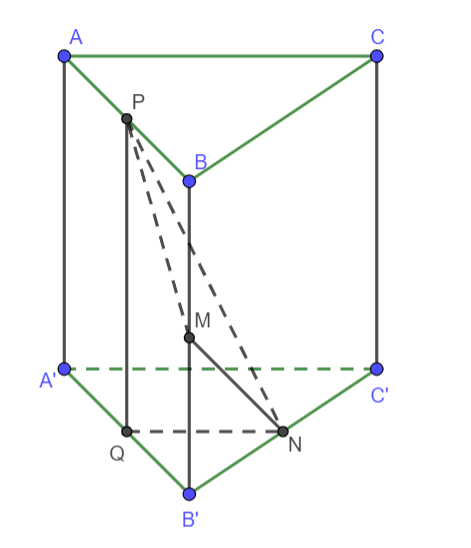
Giả sử M, N, O lần lượt là trung điểm của BB’; B’C’; AB
=> MP // AB’; MN // BC’
=> Góc cần tìm là góc giữa MP và MN
=>
Lấy Q là trung điểm của A’B’ khi đó suy ra:
Cho hình chóp ![]() có
có ![]() . Gọi hình chiếu vuông góc của điểm
. Gọi hình chiếu vuông góc của điểm ![]() lên cạnh
lên cạnh ![]() là điểm
là điểm ![]() . Xác định góc giữa hai mặt phẳng
. Xác định góc giữa hai mặt phẳng ![]() và
và ![]() ?
?
Hình vẽ minh họa
Ta có:
Vì
Vậy
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên ![]() và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ O đến mặt phẳng (SBC)
và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ O đến mặt phẳng (SBC)
Ta có:
Từ A kẻ =>
Cho hình chóp ![]() có đáy là hình vuông cạnh
có đáy là hình vuông cạnh ![]() ,
, ![]() . Tính
. Tính ![]() ?
?
Hình vẽ minh họa
Ta có: nên góc giữa
và mặt phẳng đáy bằng góc
.
Ta có:
Vậy
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, ![]() chiếu vuông góc H của S trên mặt phẳng đáy trùng với trọng tâm tam giác ABC và
chiếu vuông góc H của S trên mặt phẳng đáy trùng với trọng tâm tam giác ABC và ![]() . Gọi M và N lần lượt là trung điểm của các cạnh BC và SC. Gọi α là góc giữa đường thẳng MN với mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
. Gọi M và N lần lượt là trung điểm của các cạnh BC và SC. Gọi α là góc giữa đường thẳng MN với mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
Hình vẽ minh họa:
Ta có: MN // SB
=>
Do SH ⊥ (ABCD)
Ta có:
=>
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 2a, AD = DC = a; cạnh bên SA = a và vuông góc với đáy. Mặt phẳng (α) qua SD và vuông góc với mặt phẳng (SAC). Tính diện tích (α) của thiết diện tạo bởi (α) với hình chóp đã cho.
Hình vẽ minh họa:
Gọi E là trung điểm AB, suy ra AECD là hình vuông nên DE ⊥ AC. (1)
Mặt khác SA ⊥ (ABCD) => SA ⊥ DE (2)
Từ (1) và (2) suy ra DE ⊥ (SAC) => (SAD) ⊥ (SAC)
Ta có:
Vậy thiết diện là tam giác SDE.
Ta có:
Do đó tam giác SDE đều có cạnh a √ 2 nên
Cho một khối chóp có diện tích đáy bằng ![]() , chiều cao bằng
, chiều cao bằng ![]() . Thể tích khối chóp đã cho là:
. Thể tích khối chóp đã cho là:
Ta có:
Thể tích khối chóp là:
Cho hình lập phương ![]() . Giả sử mặt phẳng
. Giả sử mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() vuông góc với
vuông góc với ![]() . Thiết diện tạo bởi
. Thiết diện tạo bởi ![]() và hình lập phương là:
và hình lập phương là:
Hình vẽ minh họa
Ta có:
Vậy chính là mặt phẳng
. Thiết diện là một hình chữ nhật.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây sai?
Hình vẽ minh họa:
Do ABCD là hình thoi tâm O và SA = SC, SB = SD nên => SO ⊥ (ABCD)
Từ => AC ⊥ (SBD)
Từ => BD ⊥ (SAC)
Như vậy, các khẳng định “SO ⊥ (ABCD)”, “AC ⊥ (SBD)”, “BD ⊥ (SAC)” là các khẳng định đúng.
Khẳng định “BC ⊥ (SAB)” là khẳng định sai. Vì nếu BC ⊥ (SAB) suy ra BC ⊥ SB, cùng với BC ⊥ SO ta có BC ⊥ (SBD), nên qua điểm B có hai mặt phẳng phân biệt cùng vuông góc với đường thẳng BC (vô lí).
Cho hình chóp S.ABC có SA ⊥(ABC). Biết α là góc giữa SB và mặt phẳng (ABC). Xác định góc α.
Hình vẽ minh họa:
Ta có SA ⊥(ABC) => Hình chiếu của SB trên mặt phẳng (ABC) là đường thẳng AB.
=> Góc giữa đường thẳng SB và (ABC) là góc giữa hai đường thẳng SB và AB
Tức là
Cho hình chóp tứ giác đều ![]() có cạnh đáy bằng
có cạnh đáy bằng ![]() . Góc tạo bởi cạnh bên
. Góc tạo bởi cạnh bên ![]() và mặt phẳng đáy bằng
và mặt phẳng đáy bằng ![]() . Thể tích khối chóp
. Thể tích khối chóp ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
Gọi O là giao điểm của hai đường chéo AC và BD
Ta có: tam giác SAC cân, O là trung điểm của AC nên
Tương tự tam giác SBD cân, O là trung điểm của BD nên
Suy ra OA là hình chiếu vuông góc của SA lên mặt phẳng đáy
ABCD là hình vuông nên
Xét tam giác vuông SOA ta có:
Cho tứ diện ABCD có AB = AC = AD và ![]() . Hãy xác định góc giữa cặp vecto
. Hãy xác định góc giữa cặp vecto ![]() ?
?
Hình vẽ minh họa:
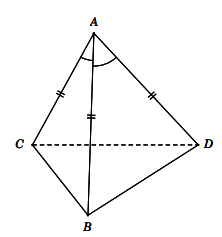
Ta có:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Dựng mặt phẳng (P) cách đều năm điểm A, B, C, D và S. Hỏi có tất cả bao nhiêu mặt phẳng (P) như vậy?
Gọi O là tâm hình bình hành ABCD.
Các mặt phẳng cách đều A, B, C, D và S là
1) Mặt phẳng qua trung điểm của SA, SB, SC, SD
2) Mặt phẳng qua O và song song (SAB)
3) Mặt phẳng qua O và song song (SAD)
4) Mặt phẳng qua O và song song (SCD)
5) Mặt phẳng qua O và song song (SBC)
Một tấm ván hình chữ nhật ![]() được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu
được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu ![]() . Cho biết
. Cho biết ![]() ,
, ![]() . Tính góc giữa đường thẳng
. Tính góc giữa đường thẳng ![]() và đáy hố. (Kết quả làm tròn đến độ).
và đáy hố. (Kết quả làm tròn đến độ).
Đáp án : 33![]()
Một tấm ván hình chữ nhật được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu
. Cho biết
,
. Tính góc giữa đường thẳng
và đáy hố. (Kết quả làm tròn đến độ).
Đáp án : 33
Gọi ,
lần lượt là hình chiếu của
,
lên đáy hố là mặt phẳng
.
Khi đó có hình chiếu lên đáy là
, suy ra
.
Với độ sâu hố là (m), ta có
.
.
.
