Lớp 11 Toán 11 - Cánh Diều

Đề thi giữa HK2 Toán 11 Cánh Diều năm học 2023 – 2024 (Đề 3)

Mô tả thêm: Đề thi giữa học kì 2 Toán 11 được biên soạn chuẩn ma trận đề thi gồm 40 các câu hỏi trắc nghiệm bám sát chương trình sách Cánh diều, giúp bạn học củng cố kiến thức chuẩn bị cho kì thi sắp tới
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Thông hiểu

    Xác định nghiệm của phương trình 4^{2x + 1} = 64?

    Ta có:

    4^{2x + 1} = 64 \Leftrightarrow 4^{2x + 1} = 4^{3}

    \Leftrightarrow 2x + 1 = 3 \Leftrightarrow x = 1(tm)

    Vậy phương trình có nghiệm x = 1.

  • Câu 2: Nhận biết

    Tập xác định của hàm số y = \log_{2}(x - 2) là:

    Điều kiện xác định của hàm số y = \log_{2}(x - 2) là:

    x - 2 > 0 \Rightarrow x > 2

    Vậy tập xác định của hàm số là D = (2; + \infty)

  • Câu 3: Thông hiểu

    Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Trực tâm của tam giác SBC và ABC lần lượt là H và K. Khẳng định nào dưới đây là khẳng định sai?

    Ta có: BC ⊥ SA, BC ⊥ SH => BC ⊥ (SAH)

    CK ⊥ AB, CK ⊥ SA => CK ⊥ (SAB) => CK ⊥ SB

    Mặt khác CH ⊥ SB => SB ⊥ (CHK)

    Ta có: BC ⊥ (SAH) => BC ⊥ HK

    SB ⊥ (CHK) => SB ⊥ HK

    => HK ⊥ (SBC)

    Dùng phương pháp loại trừ ta suy ra: BC ⊥ (SAB) là đáp án sai.

  • Câu 4: Vận dụng cao

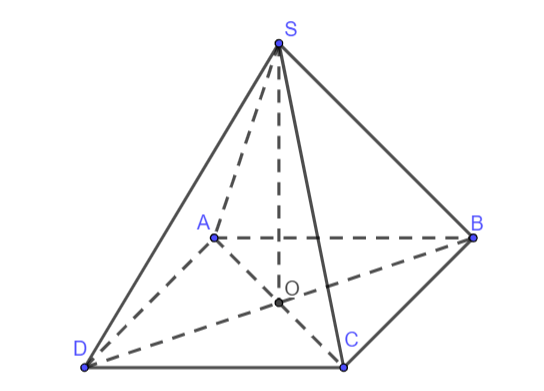
    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông cạnh A, đáy lớn AD = 8, BC = 6, SA = 6, SA ⊥ (ABCD). Gọi M là trung điểm của AB, (P) là mặt phẳng qua M và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng:

    Hình vẽ minh họa:

    Ta có: (P) ⊥ AB => (P) // SA

    Gọi I là trung điểm của SB => MI // SA => MI ⊂ (P)

    Gọi N là trung điểm của CD => MN ⊥ AB => MN ⊂ (P)

    Gọi K là trung điểm của SC => IK // BC mà MN // BC => MN // IK => IK ⊂ (P)

    Vậy thiết diện của P và hình chóp là hình thang MNKI vuông tại M

    Ta có: MI là đường trung bình của tam giác SAB => MI = \frac{1}{2}SA = 3

    IK là đường trung bình của tam giác SBC => IK = \frac{1}{2}BC = 3

    MN là đường trung bình của hình thang ABCD => MN = \frac{1}{2}(AD + BC) = 7

    => S_{MNIK} = \frac{1}{2}(MN + IK).MI = 15

  • Câu 5: Nhận biết

    Trong các kết quả dưới đây, kết quả nào là tập nghiệm của bất phương trình 2^{x} > 6?

    Ta có:

    2^{x} > 6 \Leftrightarrow x >\log_{2}6

    \Rightarrow x \in \left( \log_{2}6; +\infty ight)

    Vậy tập nghiệm của bất phương trình đã cho là \left( \log_{2}6; + \infty ight)

  • Câu 6: Vận dụng

    Trong một thí nghiệm lai tạo cây bơ, biết rằng quả tròn là tính trạng trội hoàn toàn so với quả dài. Cho cây quả tròn thuần chủng thụ phấn với cây quả dài ta được đời cây F1 toàn là cây quả tròn. Tiếp tục cho cây đời F1 thụ phấn với nhau và thu hoạch được các cây con mới. Lần lượt chọn ngẫu nhiên 2 cây con mới. Tính xác suất của biến cố trong 2 cây con mới được chọn có đúng 1 cây quả tròn?

    Quy ước gene A: quả tròn và gene a: quả dài

    Ở thế hệ F2 ba kiểu gene AA, Aa, aa xuất hiện với tỉ lệ 1: 2: 1 nên tỉ lệ quả tròn so với quả dài là 3 : 1

    Gọi A_{1} là biến cố cây được chọn lần thứ nhất là quả tròn

    A_{2} là biến cố cây được chọn lần thứ hai là quả tròn.

    Ta có: A_{1};A_{2} độc lập và P\left( A_{1} ight) = P\left( A_{2} ight) = \frac{3}{4}

    Xác suất của biến cố có đúng 1 quả tròn trong 2 cây được lấy ra:

    P\left( A_{1}\overline{A_{2}} \cup \overline{A_{1}}A_{2} ight) = P\left( A_{1}\overline{A_{2}} ight) + P\left( \overline{A_{1}}A_{2} ight)

    = P\left( A_{1} ight)P\left( \overline{A_{2}} ight) + P\left( \overline{A_{1}} ight)P\left( A_{2} ight)

    = \frac{3}{4}.\frac{1}{4} + \frac{1}{4}.\frac{3}{4} = \frac{3}{8}

  • Câu 7: Thông hiểu

    Cho hình chóp tam giác S.ABC có SA\bot(ABC);SA = a\sqrt{2}. Biết rằng tam giác ABC vuông cân tại B và AC = 2a. Tính góc giữa SB và (ABC)?

    Hình vẽ minh họa

    Ta có: SB \cap (ABC);SA\bot(ABC)

    => Hình chiếu vuông góc của SB trên mặt phẳng (ABC) là AB.

    => Góc giữa đường thẳng SB và mặt phẳng (ABC) là \widehat{SBA}

    Do tam giác ABC vuông cân tại B và AC = 2a nên AB = \frac{AC}{\sqrt{2}} = a\sqrt{2} = SA

    Suy ra tam giác SAB vuông cân tại A.

    Do đó \widehat{SBA} = 45^{0}

    Vậy góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 450.

  • Câu 8: Thông hiểu

    Có bao nhiêu giá trị nguyên của dương của tham số m để hàm số y = (6 - m)^{x} đồng biến trên tập số thực?

    Đáp án: 4

    Đáp án là:

    Có bao nhiêu giá trị nguyên của dương của tham số m để hàm số y = (6 - m)^{x} đồng biến trên tập số thực?

    Đáp án: 4

    Hàm số y = (6 - m)^{x} đồng biến trên \mathbb{R} khi và chỉ khi 6 - m > 1 \Leftrightarrow m < 5

    Mà m \in \mathbb{Z}^{+} \Rightarrow m \in \left\{ 1;2;3;4 ight\}

    Vậy có 4 giá trị của tham số m thỏa mãn điều kiện đề bài.

  • Câu 9: Thông hiểu

    Thực hiện khảo sát chi phí thanh toán cước điện thoại trong 1 tháng của cư dân trong một chung cư thu được kết quả ghi trong bảng sau:

    Số tiền (nghìn đồng)

    Số người

    [0; 50)

    5

    [50; 100)

    12

    [100; 150)

    23

    [150; 200)

    17

    [200; 250)

    3

    Chọn đáp án đúng?

    Ta có:

    Số tiền (nghìn đồng)

    Số người

    Tần số tích lũy

    [0; 50)

    5

    5

    [50; 100)

    12

    17

    [100; 150)

    23

    40

    [150; 200)

    17

    57

    [200; 250)

    3

    60

     

    N = 60

     

    Cỡ mẫu là: N = 60 \Rightarrow \frac{N}{4}= 15

    => Nhóm chứa tứ phân vị thứ nhất là [50; 100) (vì 15 nằm giữa hai tần số tích lũy 5 va 17)

    Khi đó \left\{ \begin{matrix}l = 50;\dfrac{N}{4} = 15;m = 5;f = 12 \\c = 100 - 50 = 50 \\\end{matrix} ight.

    \Rightarrow Q_{1} = l +\dfrac{\dfrac{N}{4} - m}{f}.c

    \Rightarrow Q_{1} = 50 + \frac{15 -5}{12}.50 = \frac{275}{3}

  • Câu 10: Thông hiểu

    Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và BC = a\sqrt{2}. Kết quả nào dưới đây đúng?

    Ta có:

    BC^{2} = AB^{2} + AC^{2} suy ra tam giác ABC vuông tại A

    => M là tâm đường tròn ngoại tiếp tam giác ABC.

    Vì SA = SB = SC nên SM là đường cao của hình chóp S.ABC.

    Hình vẽ minh họa

    Gọi N, I lần lượt là trung điểm cạnh AC và SB.

    Ta có: MN // AB và IM // SC nên (SC,AB) = (IM,MN)

    Mà BN = \sqrt{AB^{2} + AN^{2}} = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a\sqrt{5}}{2}

    SN = \sqrt{SC^{2} - NC^{2}} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a\sqrt{3}}{2}

    MN = \frac{a}{2};MI = \frac{a}{2}

    Xét tam giác IMN có

    \cos\widehat{NMI} = \dfrac{MN^{2} +IM^{2} - IN^{2}}{2.MN.IM}= \dfrac{\dfrac{a^{2}}{4} + \dfrac{a^{2}}{4} -\dfrac{3a^{2}}{4}}{2.\dfrac{a}{2}.\dfrac{a}{2}} = -\dfrac{1}{2}

    \Rightarrow \widehat{NMI} = 120^{0}

    \Rightarrow (SC,AB) = (IM,MN) = 60^{0}

  • Câu 11: Nhận biết

    Cho một tập hợp A gồm 12 phần tử. Hỏi số tập hợp con gồm 3 phần tử của tập hợp A bằng bao nhiêu?

    Ta có:

    Mỗi tập con gồm 3 phân tử của tập A là một tổ hợp chập 3 của 12.

    Vậy số tập con cần tìm là C_{12}^{3}.

  • Câu 12: Thông hiểu

    Trong một hộp giấy chứa 15 viên bi gồm 4 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 4 viên bi. Tính xác suất để lấy được 4 viên bi có đủ màu?

    Chọn 4 viên bi từ 15 viên bi ta có: n\left( \Omega ight) = C_{15}^4

    Gọi A là biến cố lấy được 4 viên bi có đủ ba màu.

    Chọn 1 xanh, 1 đỏ và 2 vàng: C_4^1.C_5^1.C_6^2

    Chọn 1 xanh, 2 đỏ và 1 vàng: C_4^1.C_5^2.C_6^1

    Chọn 2 xanh, 1 đỏ và 1 vàng: C_4^2.C_5^1.C_6^1

    \Rightarrow n(A) = C_{4}^{1}.C_{5}^{1}.C_{6}^{2} + C_{4}^{1}.C_{5}^{2}.C_{6}^{1} + C_{4}^{2}.C_{5}^{1}.C_{6}^{1}

    \Rightarrow P(A) = \frac{n(A)}{n(\Omega)} = \frac{48}{91}

  • Câu 13: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC, SB = SD. Khẳng định nào sau đây là đúng?

    Hình vẽ minh họa

    Khẳng định nào sau đây là đúng

    Vì SA=SC => ΔSAC cân tại S

    Mà O là trung điểm AC => SO⊥AC

    Tương tự, ta cũng có SO⊥BD mà AC∩BD=O⊂(ABCD)

    => SO⊥(ABCD)

  • Câu 14: Vận dụng cao

    Cho a,b,c > 1, biết rằng biểu thức H =\log_{a}(bc) + \log_{b}(ac) + 4\log_{c}(ab) đạt giá trị nhỏ nhất bằng m khi \log_{b}c = n. Tính giá trị của m + n.

    Do a,b,c > 1 nên \log_{a}b;\log_{b}c;\log_{c}a > 0

    Ta có:

    H = {\log _a}\left( {bc} ight) + {\log _b}\left( {ac} ight) + 4{\log _c}\left( {ab} ight)

    H = {\log _a}b + {\log _a}c + {\log _b}a + {\log _b}c + 4{\log _c}a + 4{\log _a}b

    H = \left( {{{\log }_a}b + {{\log }_b}a} ight) + \left( {{{\log }_a}c + 4{{\log }_c}a} ight) + \left( {{{\log }_b}c + 4{{\log }_a}b} ight)

    H = \left( {{{\log }_a}b + \frac{1}{{{{\log }_a}b}}} ight) + \left( {\frac{1}{{{{\log }_c}a}} + 4{{\log }_c}a} ight) + \left( {\frac{1}{{{{\log }_b}c}} + 4{{\log }_a}b} ight)

    H \geqslant 2\sqrt {{{\log }_a}b.\frac{1}{{{{\log }_a}b}}} + 2\sqrt {\frac{1}{{{{\log }_c}a}}.4{{\log }_c}a} + 2\sqrt {\frac{1}{{{{\log }_b}c}}.4{{\log }_a}b} = 2 + 4 + 4 = 10

    Dấu “=” xảy ra khi và chỉ khi

    \left\{ {\begin{array}{*{20}{c}} {{{\log }_a}b = \dfrac{1}{{{{\log }_a}b}}} \\ {\dfrac{1}{{{{\log }_c}a}} = 4{{\log }_c}a} \\ {\dfrac{1}{{{{\log }_b}c}} = 4{{\log }_a}b} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{{\log }_a}b = 1} \\ {{{\log }_c}a = \dfrac{1}{2}} \\ {{{\log }_b}c = 2} \end{array}} ight.

    Vậy H đạt giá trị nhỏ nhất là 10 khi {\log _b}c = 2 \Rightarrow \left\{ {\begin{array}{*{20}{c}} {m = 10} \\ {n = 2} \end{array}} ight. \Rightarrow m + n = 12

  • Câu 15: Nhận biết

    Xác định hàm số nghịch biến trên tập số thực trong các hàm số sau?

    Hàm số y = a^{x} nghịch biến trên \mathbb{R} khi 0 < a < 1.

  • Câu 16: Thông hiểu

    Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu?

    Hình vẽ minh họa

    Góc giữa AO và CD bằng bao nhiêu?

    Gọi M là trung điểm của CD

    Vì ABCD là tứ diện đều nên AM ⊥ CD, OM ⊥ CD

    Ta có:

    \begin{matrix} \overrightarrow {CD} .\overrightarrow {AO} = \overrightarrow {CD} .\left( {\overrightarrow {AM} + \overrightarrow {MO} } ight) \hfill \\ = \overrightarrow {CD} .\overrightarrow {AM} + \overrightarrow {CD} .\overrightarrow {MO} = \overrightarrow 0 \hfill \\ \end{matrix}

    => \overrightarrow {CD} \bot \overrightarrow {AO} nên số đo góc giữa AO và CD là 900

  • Câu 17: Nhận biết

    Biết p > 0;p eq 1. Tính \log_{p}\sqrt[1021]{p^{1022}}?

    Ta có:

    \log_{p}\sqrt[1021]{p^{1022}} =\log_{p}(p)^{\frac{1022}{1021}}

    = \frac{1022}{1021}log_{p}p = \frac{1022}{1021}

  • Câu 18: Thông hiểu

    Cho tứ diện ABCD có AC = \frac{3}{2}AD;\widehat {CAB} = \widehat {DAB} = {60^0};CD = AD. Gọi α là góc giữa AB và CD. Chọn khẳng định đúng?

     Hình vẽ minh họa:

    Chọn khẳng định đúng?

    Ta có:

    \cos (AB,CD) = \frac{{|\overrightarrow {AB} .\overrightarrow {CD} |}}{{|\overrightarrow {AB} |.|\overrightarrow {CD} |}} = \frac{{|\overrightarrow {AB} .\overrightarrow {CD} |}}{{AB.CD}}

    Mặt khác:

    \begin{matrix} \overrightarrow {AB} \cdot \overrightarrow {CD} = \overrightarrow {AB} .(\overrightarrow {AD} - \overrightarrow {AC} ) \hfill \\ = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \hfill \\ = |\overrightarrow {AB} |.|\overrightarrow {AD} |.\cos (\overrightarrow {AB} .\overrightarrow {AD} ) - |\overrightarrow {AB} |.|\overrightarrow {AC} |.\cos (\overrightarrow {AB} .\overrightarrow {AC} ) \hfill \\ = AB.AD.\cos {60^0} - AB.AC.\cos {60^0} \hfill \\ = AB.AD.\dfrac{1}{2} - AB.\dfrac{3}{2}AD.\dfrac{1}{2} \hfill \\ = - \dfrac{1}{4}AB.AD = - \dfrac{1}{4}AB.CD \hfill \\ \Rightarrow \cos (AB,CD) = \dfrac{{\left| { - \dfrac{1}{4}AB.CD} ight|}}{{AB.CD}} = \dfrac{1}{4} \hfill \\ \Rightarrow \cos \varphi = \dfrac{1}{4} \hfill \\ \end{matrix}

  • Câu 19: Thông hiểu

    Biết rằng hai số tự nhiên m,n thỏa mãn m\log_{28}2 + n\log_{28}7 = 2 . Tính tổng giá trị của m và n ?

    Đáp án: 6

    Đáp án là:

    Biết rằng hai số tự nhiên m,n thỏa mãn m\log_{28}2 + n\log_{28}7 = 2 . Tính tổng giá trị của m và n ?

    Đáp án: 6

    Ta có:

    m\log_{28}2 + n\log_{28}7 = 2

    \Leftrightarrow \log_{28}\left(2^{x}.7^{y} ight) = 2 \Leftrightarrow 2^{x}.7^{y} =28^{2}

    \Leftrightarrow 2^{x}.7^{y} = \left(2^{2}.7 ight)^{2} \Leftrightarrow 2^{x}.7^{y} =2^{4}.7^{2}

    \Leftrightarrow \left\{ \begin{matrix}x = 4 \\y = 2 \\\end{matrix} ight.\ \Rightarrow x + y = 6

  • Câu 20: Nhận biết

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1, tam giác SAD là tam giác đều. Tìm sin của góc tạo bởi hai đường thẳng SA và BC.

    Hình vẽ minh họa

    Ta có: BC//AD \Rightarrow (BC;SA) = (BD;SA) = \widehat{SAD} = 60^{0}

    \Rightarrow \sin(BC;SA) = \frac{\sqrt{3}}{2}

  • Câu 21: Vận dụng

    Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau và AB = a, BC = b, CD = c. Độ dài đoạn thẳng AD bằng bao nhiêu?

    Hình vẽ minh họa:

    Ta có: \left\{ \begin{matrix} BC\bot AB \\ CD\bot AB \\ \end{matrix} ight.\ \Rightarrow AB\bot(BCD)

    => Tam giác ABD vuông tại B.

    Ta có: \left\{ \begin{matrix} CD\bot AB \\ CD\bot BC \\ \end{matrix} ight.\ \Rightarrow CD\bot(ABC)

    => Tam giác BCD vuông tại C.

    Ta có: \left\{ \begin{matrix} AD^{2} = AB^{2} + BD^{2} \\ BD^{2} = BC^{2} + CD^{2} \\ \end{matrix} ight.

    \begin{matrix}\Rightarrow AD^{2} = AB^{2} + BC^{2} + CD^{2} \hfill \\\Rightarrow AD = \sqrt{AB^{2} + BC^{2} + CD^{2}} \hfill \\\Rightarrow AD = \sqrt{a^{2} + b^{2} + c^{2}} \hfill \\\end{matrix}

  • Câu 22: Nhận biết

    Kết quả khảo sát cân nặng tất cả học sinh trong lớp 11H được ghi trong bảng sau:

    Cân nặng (kg)

    Số học sinh

    [45; 50)

    5

    [50; 55)

    12

    [55; 60)

    10

    [60; 65)

    6

    [65; 70)

    5

    [70; 75)

    8

    Cỡ mẫu của mẫu số liệu là:

    Cỡ mẫu của mẫu số liệu là:

    N = 5 + 12 + 10 + 6 + 5 + 8 = 46

  • Câu 23: Thông hiểu

    Cho hình chóp S.ABC có SA = SB = SC và \widehat {ASB} = \widehat {BSC} = \widehat {CSA}. Góc giữa cặp vecto \overrightarrow {SA} ;\overrightarrow {BC} là:

     \begin{matrix} \overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .\left( {\overrightarrow {SC} - \overrightarrow {SB} } ight) \hfill \\ = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \hfill \\ = \left| {\overrightarrow {SA} } ight|.\left| {\overrightarrow {SC} } ight|\cos \widehat {ASC} - \left| {\overrightarrow {SA} } ight|.\left| {\overrightarrow {SB} } ight|\cos \widehat {ASB} \hfill \\ = 0 \hfill \\ \Rightarrow SA \bot BC \hfill \\ \end{matrix}

  • Câu 24: Thông hiểu

    Tìm hiểu thời gian tập thể dục mỗi ngày của học sinh (đơn vị: phút) ta thu được kết quả ghi trong bảng sau:

    Thời gian (phút)

    [0; 5)

    [5; 10)

    [10; 15)

    [15; 20)

    [20; 25)

    Số học sinh

    8

    16

    4

    7

    12

    Hỏi số học sinh tập thể dục ít nhất 10 phút mỗi ngày chiếm bao nhiêu phần trăm?

    Số học sinh tập thể dục ít nhất 10 phút mỗi ngày là:

    4 + 7 + 12 = 23 (học sinh) chiếm \frac{23.100\%}{47} \approx49\%

  • Câu 25: Nhận biết

    Cho biết \log_{2}a= x;\log_{2}b = y, biểu thức \log_{2}\left( 4a^{2}b^{3} ight) có giá trị là:

    Ta có:

    \log_{2}\left( 4a^{2}b^{3} ight) =\log_{2}4 + \log_{2}a^{2} + \log_{2}b^{3}

    = 2 + 2\log_{2}a + 3\log_{2}b = 2x + 3y +2

  • Câu 26: Thông hiểu

    Phương trình 3\log_{3}(x - 1) - \log_{\frac{1}{3}}(x - 5)^{3} =3 có bao nhiêu nghiệm nguyên?

    Điều kiện x > 5

    Ta có:

    3\log_{3}(x - 1) - \log_{\frac{1}{3}}(x -5)^{3} = 3

    \Leftrightarrow 3\log_{3}(x - 1) +3\log_{3}(x - 5) = 3

    \Leftrightarrow \log_{3}(x - 1) +\log_{3}(x - 5) = 1

    \Leftrightarrow \log_{3}\left\lbrack (x -1).(x - 5) ightbrack = 1

    \Leftrightarrow (x - 1).(x - 5) = 3^{1}

    \Leftrightarrow x^{2} - 6x + 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 3 + \sqrt{7} \\ x = 3 - \sqrt{7} \\ \end{matrix} ight.\ (ktm) (vì nghiệm cần xét là nghiệm nguyên)

    Vậy phương trình không có nghiệm nguyên.

  • Câu 27: Vận dụng

    Cho a là một số thực dương khác 1. Tính giá trị của biểu thức:

    P = \log_{a}2018 + \log_{\sqrt{a}}2018 +\log_{\sqrt[3]{a}}2018 + ... + \log_{\sqrt[2018]{a}}2018

    Ta có:

    P = \log_{a}2018 + \log_{\sqrt{a}}2018 +\log_{\sqrt[3]{a}}2018 + ... + \log_{\sqrt[2018]{a}}2018

    P = \log_{a}2018 + 2\log_{a}2018 +3\log_{a}2018 + ... + 2018\log_{a}2018

    P = \log_{a}2018(1 + 2 + 3 + .... +2018)

    P = \log_{a}2018.\frac{(1 +2018).2018}{2}

    P = 1009.2019.\log_{a}2018

  • Câu 28: Nhận biết

    Em hãy mô tả không gian mẫu của phép thử gieo một con xúc xắc là:

    Không gian mẫu của phép thử gieo một con xúc xắc cân đối đồng chất là: \Omega = \left\{ 1;2;3;4;5;6 ight\}

  • Câu 29: Nhận biết

    Mệnh đề nào sau đây đúng?

    Mệnh đề đúng là: Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì có thể vuông góc với nhau

  • Câu 30: Nhận biết

    Mệnh đề nào sau đây đúng?

    Mệnh đề đúng là: Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì có thể vuông góc với nhau

  • Câu 31: Thông hiểu

    Đề thi Hóa học thi THPT Quốc Gia gồm 50 câu trắc nghiệm, mỗi câu có 4 đáp án trắc nghiệm và chỉ có duy nhất 1 đáp án đúng. Mỗi câu trả lời đúng được 0,2 điểm. Bạn Phong đã làm đúng 40 câu và trả lời ngẫu nhiên cho 10 câu hỏi còn lại. Hỏi xác suất để Phong đạt trên 8,5 điểm?

    Vì mỗi câu có 4 phương án trả lời và chỉ có đúng 1 phương án đúng nên xác suất để chọn đúng đáp án là \frac{1}{4}; xác suất trả lời sai là \frac{3}{4}

    Gọi A là biến cố bạn Phong được trên 8,5 điểm thì \overline{A} là biến cố bạn Phong được dưới 8,5 điểm.

    Vì bạn Phong đã làm chắc chắn đúng 40 câu nên để có \overline{A} xảy ra 2 trường hợp:

    TH1: Bạn Phong chọn được một câu đúng trong 10 câu còn lại xác suất xảy ra là: 10.\frac{1}{4}.\left( \frac{3}{4} ight)^{9}

    TH2: Bạn Phong chọn được hai câu đúng trong 10 câu còn lại xác suất xảy ra là: C_{10}^{2}.\left( \frac{1}{4} ight)^{2}.\left( \frac{3}{4} ight)^{8}

    \Rightarrow P(A) = 1 - P\left( \overline{A} ight)

    = 1 - \left\lbrack 10.\frac{1}{4}.\left( \frac{3}{4} ight)^{9} + C_{10}^{2}.\left( \frac{1}{4} ight)^{2}.\left( \frac{3}{4} ight)^{8} ightbrack \approx 0,53

  • Câu 32: Nhận biết

    Thực hiện khảo sát chi phí thanh toán cước điện thoại trong 1 tháng của cư dân trong một chung cư thu được kết quả ghi trong bảng sau:

    Số tiền (nghìn đồng)

    Số người

    [0; 50)

    5

    [50; 100)

    12

    [100; 150)

    23

    [150; 200)

    17

    [200; 250)

    3

    Nhóm nào chứa mốt của mẫu số liệu?

    Nhóm chứa mốt của dấu hiệu là: [100; 150)

  • Câu 33: Nhận biết

    Một nhóm học sinh gồm 15 người. Cần chọn 3 người lần lượt làm các chức vụ nhóm trưởng, nhóm phó và kiểm soát. Số cách chọn là:

    Số cách chọn 3 người đảm nhiệm 3 chức vụ khác nhau từ 15 người là:

    A_{15}^{3} = 2730 (cách)

    Vậy có tất cả 2730 cách chọn.

  • Câu 34: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a tâm I, SA vuông góc với mặt phẳng đáy. Biết SA = a\sqrt{3};\beta = \left( SI;(ABCD) ight). Tính \tan\beta?

    Hình vẽ minh họa

    Ta có: SA\bot(ABCD) nên AI là hình chiếu vuông góc của SI trên mặt phẳng đáy.

    Do đó góc giữa đường thẳng SI và mặt phẳng (ABCD) bằng góc giữa SI và AI.

    Xét tam giác SAI vuông tại A nên \widehat{SIA} < 90^{0} \Rightarrow (SI;AI) = \widehat{SIA}

    \tan\widehat{SIA} = \dfrac{SA}{AI} =\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{2}}{2}} = \sqrt{6}

    Vậy \tan\beta = \sqrt{6}

  • Câu 35: Nhận biết

    Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA\bot(ABCD);SA = a\sqrt{2}. Tính \left( SC;(ABCD) ight)?

    Hình vẽ minh họa

    Ta có: SA\bot(ABCD) nên góc giữa SC và mặt phẳng đáy bằng góc \widehat{SCA}.

    Ta có: SA = a\sqrt{2};AC = a\sqrt{2}

    \Rightarrow \tan\widehat{SCA} = \frac{SA}{AC} = 1 \Rightarrow \widehat{SCA} = 45^{0}

    Vậy \left( SC;(ABCD) ight) = 45^{0}

  • Câu 36: Vận dụng

    Cho hàm số y =\log_{a}x;y = \log_{b}x có đồ thị như hình vẽ:

    Đường thẳng x = 7 cắt trục hoành, đồ thị hàm số y = \log_{a}x;y =\log_{b}x lần lượt tại H,M,N. Biết rằng HM = MN. Khẳng định nào sau đây đúng?

    Ta có:\left\{ \begin{matrix}HM = y_{M} = \log_{a}7 \\MN = y_{N} - y_{M} = \log_{b}7 - \log_{a}7 \\\end{matrix} ight.

    Mặt khác HM = MN nên \log_{b}7 - \log_{a}7 = \log_{a}7

    \Leftrightarrow \log_{b}7 =\log_{\sqrt{a}}7

    \Leftrightarrow b = \sqrt{a} \Leftrightarrow b^{2} = a

  • Câu 37: Thông hiểu

    Ta có: \sqrt[3]{x^{5}\sqrt{x^{2}\sqrt{x}}} = x^{\alpha}. Giá trị \alpha là:

    Ta có:

    \sqrt[3]{x\sqrt[5]{x^{2}\sqrt{x}}} = \sqrt[3]{x\sqrt[5]{x^{2}.x^{\frac{1}{2}}}} = \sqrt[3]{x\sqrt[5]{x^{\frac{5}{2}}}} = \sqrt[3]{x^{\frac{3}{2}}} = x^{\frac{1}{2}}

    \Rightarrow \alpha = \frac{1}{2}

  • Câu 38: Nhận biết

    Với a là số thực dương tùy ý, a^{4}.a^{\frac{1}{2}} bằng:

    Ta có:

    a^{4}.a^{\frac{1}{2}} = a^{4 + \frac{1}{2}} = a^{\frac{9}{2}}

  • Câu 39: Nhận biết

    “Mẫu số liệu … là mẫu số liệu cho dưới dạng bảng tần số của các nhóm số liệu.”. Cụm từ thích hợp để điền vào “…” là: Ghép nhóm||Không ghép nhóm|| Ghép nhóm và không ghép nhóm

    Đáp án là:

    “Mẫu số liệu … là mẫu số liệu cho dưới dạng bảng tần số của các nhóm số liệu.”. Cụm từ thích hợp để điền vào “…” là: Ghép nhóm||Không ghép nhóm|| Ghép nhóm và không ghép nhóm

    Hoàn thành câu: Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số của các nhóm số liệu.

  • Câu 40: Thông hiểu

    Cho hình chóp tam giác S.ABC có ABC vuông tại B và SA\bot(ABC). Kẻ đường cao AH của tam giác SAB. Khẳng định nào dưới đây là khẳng định sai?

    Hình vẽ minh họa

    Ta có: SA\bot(ABC) \Rightarrow SA\bot BC

    Ta có: \left\{ \begin{matrix} BC\bot AB(gt) \\ BC\bot SA;\left( do\ SA\bot(ABC) ight) \\ \end{matrix} ight.

    \Rightarrow BC\bot(SAB) \Rightarrow BC\bot AH

    Mà AH\bot SB \Rightarrow AH\bot(SBC)

    \Rightarrow \left\{ \begin{matrix} AH\bot SC \\ AH\bot BC \\ \end{matrix} ight.

    Vậy khẳng định sai là: “AH\bot AC”.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi giữa HK2 Toán 11 Cánh Diều năm học 2023 – 2024 (Đề 3) Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi giữa HK2 Toán 11 Cánh Diều năm học 2023 – 2024 (Đề 3)
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập