Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, ![]() chiếu vuông góc H của S trên mặt phẳng đáy trùng với trọng tâm tam giác ABC và
chiếu vuông góc H của S trên mặt phẳng đáy trùng với trọng tâm tam giác ABC và ![]() . Gọi M và N lần lượt là trung điểm của các cạnh BC và SC. Gọi α là góc giữa đường thẳng MN với mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
. Gọi M và N lần lượt là trung điểm của các cạnh BC và SC. Gọi α là góc giữa đường thẳng MN với mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
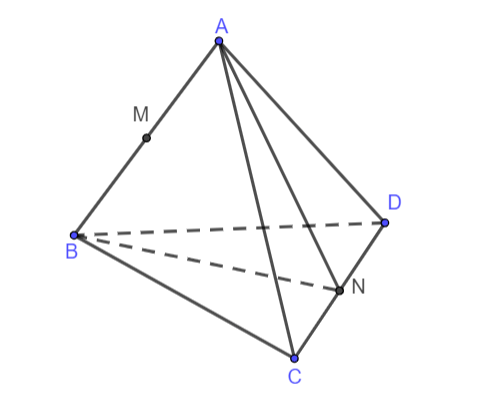
Hình vẽ minh họa:
Ta có: MN // SB
=>
Do SH ⊥ (ABCD)
Ta có:
=>








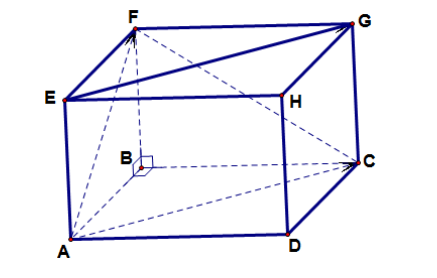
 . Tính
. Tính 