Đề thi giữa HK2 Toán 11 Kết nối tri thức năm học 2023 – 2024 (Đề 5)

Mô tả thêm: Đề thi giữa HK2 Toán 11 được biên soạn chuẩn ma trận đề thi gồm 40 các câu hỏi trắc nghiệm bám sát chương trình sách Kết nối tri thức, giúp bạn học củng cố kiến thức chuẩn bị cho kì thi sắp tới

Thời gian làm: 90 phút
Số câu hỏi: 40 câu
Số điểm tối đa: 40 điểm
Tài khoản: Đăng nhập

Mua gói để Làm bài

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Câu 1: Vận dụng cao
Cho tứ diện ABCD có độ dài các cạnh AB = a, AD = BC = b, AB là đoạn vuông góc chung của BC và AD và (AB, CD) = α, 0⁰ < α < 90⁰, tan α < $\frac{2b}{a}$ . Gọi I là trung điểm AB, điểm M thuộc đoạn AB sao cho IM = x và (P) là mặt phẳng đi qua M vuông góc với AB đồng thời cắt CD tại N. Diện tích hình tròn tâm M bán kính MN bằng
- A.
  $\frac{\pi}{4}\left\lbrack 4b^{2} +\left( 4x^{2} - a^{2} ight)tan^{2}\alphaightbrack$
- B.
  $\pi\left\lbrack 4b^{2} + \left(4x^{2} - a^{2} ight)tan^{2}\alpha ightbrack$
- C.
  $\frac{\pi}{4}\left\lbrack 2b^{2} +\left( 4x^{2} + a^{2} ight)tan^{2}\alphaightbrack$
- D.
  $\frac{\pi}{4}\left\lbrack 4b^{2} +\left( 4x^{2} - a^{2} ight)sin^{2}\alphaightbrack$
Hình vẽ minh họa:
Dựng hình lăng trụ đứng tam giác ADE.BFC như hình vẽ, trong đó AB là cạnh bên.
Khi đó mặt phẳng (P) song song với hai mặt phẳng đáy của hình lăng trụ nói trên.
Gọi P, Q lần lượt là giao điểm của (P) với CE và DF.
Không mất tính tổng quát, giả sử M thuộc đoạn AI.
Ta có $\widehat{CDF}$ = (CD, DF) = (CD, AB) = α, suy ra PQ = CF = a tan α.
Do đó:
$\begin{matrix}\dfrac{NQ}{CF} = \dfrac{DQ}{DF} = \dfrac{AM}{AB} = \dfrac{a - 2x}{2a} \hfill\\\Rightarrow NQ = \dfrac{(a - 2x)\tan\alpha}{2} \hfill \\\Rightarrow \cos\widehat{MQP} = \dfrac{MQ^{2} + PQ^{2} - MP^{2}}{2MQ.PQ} \hfill\\= \dfrac{PQ}{2MQ} = \dfrac{a\tan\alpha}{2b} \hfill\\MN^{2} = MQ^{2} + NQ^{2} - 2MQ.NQ \hfill\\\Rightarrow \cos\widehat{MQN} = \dfrac{4b^{2} + \tan^{2}\alpha\left(4x^{2} - a^{2} ight)}{4} \hfill\\\end{matrix}$
Vậy $\frac{\pi}{4}\left\lbrack 4b^{2} +\left( 4x^{2} - a^{2} ight)tan^{2}\alphaightbrack$
Câu 2: Vận dụng
Số $20172018^{20162017}$ có bao nhiêu chữ số?
- A.
  $147278481$
- B.
  $147278480$
- C.
  $147347190$
- D.
  $147347191$
Số tự nhiên $M$ có $k$ chữ số khi

$10^{k - 1} \leq M \leq 10^{k}$

Đặt $M = 20172018^{20162017}$ suy ra

$\log M = \log\left( 20172018^{20162017} ight)$

$\Leftrightarrow M = 10^{\log\left( 20172018^{20162017} ight)}$

$\Leftrightarrow M = 10^{20162017.log(20172018)}$

$\Leftrightarrow M \approx 10^{1147278480,5} < 10^{147278481}$

Vậy số các chữ số của $20172018^{20162017}$ là 147278481.
Câu 3: Thông hiểu
Cho đồ thị hàm số:
Xác định hàm số tương ứng?
- A.
  $y = 3^{x}$
- B.
  $y = \left( \frac{1}{3}ight)^{x}$
- C.
  $y = \left( \frac{1}{2}ight)^{x}$
- D.
  $y = 2^{x}$
Đồ thị hàm số đi lên và qua điểm có tọa độ $(1;3)$ nên hàm số thỏa mãn là $y = 3^{x}$
Câu 4: Thông hiểu
Cho tứ diện ABCD có AB = AC = AD và $\widehat {BAC} = \widehat {BAD} = {60^0};\widehat {CAD} = {90^0}$ . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vecto $\overrightarrow {AB} ;\overrightarrow {IJ}$ ?
- A. 120⁰
- B. 90⁰
- C. 60⁰
- D. 45⁰
Hình vẽ minh họa:
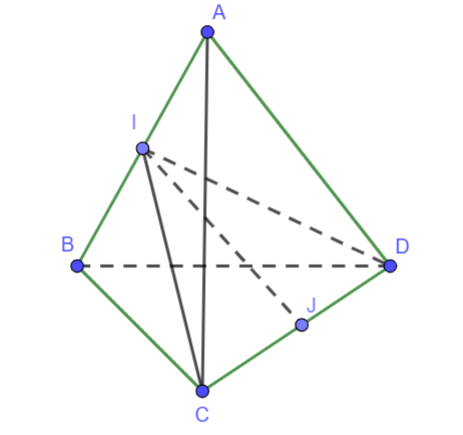
Xét tam giác ICD có J là trung điểm của CD => $\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {JC} + \overrightarrow {ID} } ight)$
Tam giác ABC có AB = AC và $\widehat {BAC} = {60^0}$ => Tam giác ABC đều => CI ⊥ AB
Tương tự ta chứng minh được tam giác aBD đều => DI ⊥ AB
Ta có:
$\begin{matrix} \overrightarrow {AB} .\overrightarrow {IJ} = \dfrac{1}{2}\overrightarrow {AB} .(\overrightarrow {IC} + \overrightarrow {ID} ) \hfill \\ = \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {IC} + \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {ID} = 0 \hfill \\ \Rightarrow \overrightarrow {AB} \bot \overrightarrow {IJ} \Rightarrow \left( {\overrightarrow {AB} ;\overrightarrow {IJ} } ight) = {90^0} \hfill \\ \end{matrix}$
Câu 5: Vận dụng
Cho biểu thức $D =\left\lbrack \dfrac{x^{\frac{1}{2}} - a^{\frac{3}{2}}}{x^{\frac{1}{2}} -a^{\frac{1}{2}}} + (ax)^{\frac{1}{2}} ightbrack.\left(\dfrac{x^{\frac{1}{2}} - a^{\frac{1}{2}}}{x - a} ight)$ . Khẳng định nào sau đây đúng?
- A.
  $D = - 1$
- B.
  $D = \frac{1}{\sqrt{x} + \sqrt{a}}$
- C.
  $D = \sqrt{x - a}$
- D.
  $D = 1$
Ta có:

$D = \left\lbrack \frac{x^{\frac{1}{2}} - a^{\frac{3}{2}}}{x^{\frac{1}{2}} - a^{\frac{1}{2}}} + (ax)^{\frac{1}{2}} ightbrack.\left( \frac{x^{\frac{1}{2}} - a^{\frac{1}{2}}}{x - a} ight)$

$= \left\lbrack \frac{\left( x^{\frac{1}{2}} ight)^{3} - \left( a^{\frac{1}{2}} ight)^{3}}{x^{\frac{1}{2}} - a^{\frac{1}{2}}} + (ax)^{\frac{1}{2}} ightbrack^{2}.\left\lbrack \frac{x^{\frac{1}{2}} - a^{\frac{1}{2}}}{\left( x^{\frac{1}{2}} ight)^{2} - \left( a^{\frac{1}{2}} ight)^{2}} ightbrack$

$= \left\lbrack \frac{\left( x^{\frac{1}{2}} - a^{\frac{1}{2}} ight)\left( \left( x^{\frac{1}{2}} ight)^{2} + x^{\frac{1}{2}}a^{\frac{1}{2}} + \left( a^{\frac{1}{2}} ight)^{2} ight)}{x^{\frac{1}{2}} - a^{\frac{1}{2}}} + (ax)^{\frac{1}{2}} ightbrack\left\lbrack \frac{x^{\frac{1}{2}} - a^{\frac{1}{2}}}{\left( x^{\frac{1}{2}} - a^{\frac{1}{2}} ight)\left( x^{\frac{1}{2}} + a^{\frac{1}{2}} ight)} ightbrack$

$= \left\lbrack \left( x^{\frac{1}{2}} ight)^{2} + 2x^{\frac{1}{2}}a^{\frac{1}{2}} + \left( a^{\frac{1}{2}} ight)^{2} ightbrack\left( \frac{1}{x^{\frac{1}{2}} + a^{\frac{1}{2}}} ight)^{2}$

$= \left( x^{\frac{1}{2}} + a^{\frac{1}{2}} ight)^{2}\left( \frac{1}{x^{\frac{1}{2}} + a^{\frac{1}{2}}} ight)^{2} = 1$
Câu 6: Nhận biết
Xác định nghiệm của bất phương trình $5^{x - 2} \leq \frac{1}{5}$ ?
- A.
  $\lbrack 1; + \infty)$
- B.
  $( - \infty;0)$
- C.
  $\lbrack 2; + \infty)$
- D.
  $( - \infty;1brack$
Ta có:

$5^{x - 2} \leq \frac{1}{5} \Leftrightarrow 5^{x - 2} \leq 5^{- 1}$

$\Leftrightarrow x - 2 \leq - 1 \Leftrightarrow x \leq 1$ hay $x \in ( - \infty;1brack$
Câu 7: Nhận biết
Biết $a \in \mathbb{R}^{+}$ , $\sqrt{a^{3}}$ bằng:
- A.
  $a^{\frac{1}{6}}$
- B.
  $a^{\frac{2}{3}}$
- C.
  $a^{6}$
- D.
  $a^{\frac{3}{2}}$
Ta có: $\sqrt{a^{3}} = a^{\frac{3}{2}}$
Câu 8: Nhận biết
Hình chóp tam giác đều $S.ABC$ . Gọi $G$ là trọng tâm tam giác $ABC$ . Khẳng định nào sau đây đúng?
- A.
  $SA\bot(ABC)$
- B.
  $SG\bot(ABC)$
- C.
  $AB\bot(ASC)$
- D.
  $SG\bot(ABS)$
Ta có khối chóp tam giác đều $S.ABC$ có đáy $ABC$ là tam giác đều, trọng tâm G cũng là tâm của đáy nên $SG\bot(ABC)$ .
Câu 9: Nhận biết
Cho hình chóp tứ giác $S.ABCD$ có $SA\bot(ABCD)$ và đáy là hình vuông. Chọn kết luận đúng?
- A.
  $BC\bot(SAB)$
- B.
  $AC\bot(SAD)$
- C.
  $AC\bot(SBD)$
- D.
  $AC\bot(SAB)$
Hình vẽ minh họa

Ta có: $SA\bot(ABCD) \Rightarrow SA\bot BC$

Ta có: $\left\{ \begin{matrix} SA\bot BC \\ AB\bot BC \\ \end{matrix} ight.\ \Rightarrow BC\bot(SAB)$
Câu 10: Nhận biết
Có bao nhiêu cách lấy hai con bài từ cỗ bài tú lơ khơ gồm 52 con?
- A. 104
- B. 450
- C. 1326
- D. 2652
Mỗi cách lấy 2 con bài từ 52 con là một tổ hợp chập 2 của 52 phần tử.
Vậy số cách lấy hai con bài từ cỗ bài tú lơ khơ 52 con là $C_{52}^2 = 1326$ cách.
Câu 11: Nhận biết
Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Chọn mô tả đúng dưới đây?
- A.
  $\Omega = \left\{ (a;b)|a,b \in \left\{ 1;2;3;4;5 ight\} ight\}$
- B.
  $\Omega = \left\{ (a;b)|a,b \in \left\{ 1;2;3;4;5;6 ight\} ight\}$
- C.
  $\Omega = \left\{ (a;b)|a,b \in \left\{ 1;2;3;4;5 ight\};a eq b ight\}$
- D.
  $\Omega = \left\{ (a;b)|a,b \in \left\{ 1;2;3;4;5;6 ight\};a eq b ight\}$
Mô tả không gian mẫu đúng là: $\Omega = \left\{ (a;b)|a,b \in \left\{ 1;2;3;4;5;6 ight\} ight\}$
Câu 12: Vận dụng
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ , $SA$ vuông góc với mặt phẳng đáy, $SA = a$ . Gọi $M$ là trung điểm của $SD$ và $\alpha$ là góc giữa hai đường thẳng $AC$ và $BM$ . Chọn kết luận đúng?
- A.
  $\cos\alpha = \frac{\sqrt{6}}{3}$
- B.
  $\cos\alpha = \frac{1}{\sqrt{3}}$
- C.
  $\cos\alpha = \frac{\sqrt{3}}{6}$
- D.
  $\cos\alpha = \frac{\sqrt{2}}{6}$
Hình vẽ minh họa

Gọi O là giao điểm của AC và BD, I là giao điểm của SO và BM.

Trong mặt phẳng (SAC) kẻ NK // AC, $NK \cap SA = N;NK \cap SC = K$

Ta có: I là trọng tâm tam giác SBD.

Ta có: $SO = \sqrt{SA^{2} + AO^{2}} = \frac{a\sqrt{3}}{2}$

Tam giác SBD đều cạnh bằng $a\sqrt{2} \Rightarrow BM = \frac{a\sqrt{2}.\sqrt{3}}{2} = \frac{a\sqrt{6}}{2} \Rightarrow BI = \frac{2}{3}MB = \frac{a\sqrt{6}}{3}$

$\Rightarrow \frac{IK}{OC} = \frac{2}{3} \Rightarrow IK = \frac{2}{3}OC = \frac{2}{3}.\frac{a\sqrt{2}}{2} = \frac{a\sqrt{2}}{3}$

$\frac{SK}{SC} = \frac{2}{3} \Rightarrow SK = \frac{2}{3}SC = \frac{2}{3}.a\sqrt{3}$

Tam giác SBC vuông tại B $\Rightarrow \cos\widehat{SBC} = \frac{SB}{SC} = \frac{a\sqrt{2}}{a\sqrt{3}} = \frac{\sqrt{6}}{3}$

Lại có:

$KB^{2} = SK^{2} + SB^{2} - 2SK.SB.cos\widehat{BSK}$

$= \left( \frac{2a\sqrt{3}}{3} ight)^{2} + 2a^{2} - 2.\frac{2a\sqrt{3}}{3}.a\sqrt{2}.\frac{\sqrt{6}}{3} = \frac{2}{3}a^{2}$

$\Rightarrow \cos\widehat{KIB} = \frac{IK^{2} + IB^{2} - KB^{2}}{2.IK.IB}$

$= \frac{\left( \frac{a\sqrt{2}}{3} ight)^{2} + \left( \frac{a\sqrt{6}}{3} ight)^{2} - \frac{2a^{2}}{3}}{2.\frac{a\sqrt{2}}{3}.\frac{a\sqrt{6}}{3}} = \frac{1}{2\sqrt{3}} = \frac{\sqrt{3}}{6}$

Vậy cosin góc giữa hai đường thẳng $AC$ và $BM$ là $\frac{\sqrt{3}}{6}$ .

VD

1
Câu 13: Thông hiểu
Cho hai số thực dương $a,b$ . Tính giá trị biểu thức: $M = \log_{\sqrt{2}}a - \log_{2}b$ biết $a^{2} - 16b = 0$ ?
- A.
  $M = 2$
- B.
  $M = 4$
- C.
  $M = 16$
- D.
  $M = 8$
Ta có: $a^{2} - 16b = 0 \Rightarrow b = \frac{a^{2}}{16}$

$M = \log_{\sqrt{2}}a - \log_{2}b =\log_{\sqrt{2}}a - \log_{2}\frac{a^{2}}{16}$

$= 2\log_{a}a - 2\log_{2}a + \log_{2}16 =\log_{2}16 = 4$
Câu 14: Vận dụng
Trong một tuần bạn A dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình thăm một bạn không quá một lần
- A. 3991680
- B. 12!
- C. 35831808
- D. 7!
Một tuần có bảy ngày và mỗi ngày thăm một bạn.
Có 12 cách chọn bạn vào ngày thứ nhất.
Có 11 cách chọn bạn vào ngày thứ hai.
Có 10 cách chọn bạn vào ngày thứ ba.
Có 9 cách chọn bạn vào ngày thứ tư.
Có 8 cách chọn bạn vào ngày thứ năm.
Có 7 cách chọn bạn vào ngày thứ sáu.
Có 6 cách chọn bạn vào ngày thứ bảy.
Vậy theo quy tắc nhân ta có 12.11.10.9.8.7.6 = 3991680 cách.
Câu 15: Thông hiểu
Tìm tất cả các giá trị thực của tham số m để hàm số $f(x) = \left( 1 + \ln might)^{x}$ đồng biến trên tập số thực.
- A.
  $\frac{1}{e} < m < 1$
- B.
  $m> 1$
- C.
  $m > 0$
- D.
  $m > e$
Ta có hàm số $f(x) = \left( 1 + \ln m ight)^{x}$ đồng biến trên $\mathbb{R}$

Khi và chỉ khi $1 + \ln m > 1\Leftrightarrow m > 1$
Câu 16: Nhận biết
Tính giá trị biểu thức $M = 2^{\log_{2}a} + \log_{a}\left( a^{b}ight)$ với điều kiện $a > 0;a eq 1$ ?
- A.
  $M = 2^{a} + b$
- B.
  $M = a + b$
- C.
  $M = 2a + b$
- D.
  $M = a - 2b$
Ta có:

$M = 2^{\log_{2}a} + \log_{a}\left( a^{b}ight) = a + b$
Câu 17: Nhận biết
Biết $\forall n \in \mathbb{R}^{+}$ . Kết luận nào dưới đây đúng?
- A.
  $\log_{4}n^{4} = 4$
- B.
  $\log_{4}n^{4} =\frac{1}{4}\log_{4}n$
- C.
  $\log_{4}n^{4} = 4\log_{4}n$
- D.
  $\log_{4}n^{4} =\frac{1}{4}$
Ta có: $\log_{4}n^{4} = 4\log_{4}|n| =4\log_{4}n$
Câu 18: Nhận biết
Cho hình lập phương $ABCD.A'B'C'D'$ . Góc giữa hai đường thẳng $A'B$ và $AD'$ bằng:
- A.
  $90^{0}$
- B.
  $45^{0}$
- C.
  $60^{0}$
- D.
  $30^{0}$
Hình vẽ minh họa

Ta có: $A'B//D'C$ nên góc giữa hai đường thẳng $A'B$ và $AD'$ bằng góc giữa hai đường thẳng $D'C$ và $AD'$ và bằng góc $\widehat{AD'C}$

Mà tam giác ACD’ là tam giác đều nên $\widehat{AD'C} = 60^{0}$

$\Rightarrow (A'B;AD') = 60^{0}$
Câu 19: Vận dụng
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = a;AD = 2a;AA' = a\sqrt{2}$ . Gọi mặt phẳng $(\alpha)$ qua $A$ và vuông góc với $A'B$ . Tính diện tích thiết diện tạo bởi $(\alpha)$ và hình hộp chữ nhật đã cho?
- A.
  $\frac{a^{2}\sqrt{3}}{2}$
- B.
  $2a^{2}$
- C.
  $a^{2}\sqrt{2}$
- D.
  $a^{2}\sqrt{6}$
Hình vẽ minh họa

Hình chữ nhật $ABB'A'$ có $AB = a;AA' = a\sqrt{2}$ . Lấy $M$ là trung điểm của $BB'$ . Ta dễ dàng chứng minh $AM\bot A'B$

Ta lại có $AD\bot A'B$ suy ra mặt phẳng $(\alpha)$ chính là mặt phẳng $(ADM)$ .

Qua điểm M kẻ MN // AD. Thiết diện khi đó là hình chữ nhật ADMN.

Ta tính được $AM = \frac{a\sqrt{6}}{2};AD = 2a$

Suy ra diện tích hình chữ nhật ADMN là: $a^{2}\sqrt{6}$ .
Câu 20: Nhận biết
Biết $m,n$ là hai số dương tùy ý thì $\log\left( m^{3}n^{2} ight)$ có giá trị tương ứng với biểu thức nào sau đây?
- A.
  $3\log m + 2\log n$
- B.
  $3\log m + \frac{1}{2}\log n$
- C.
  $2\log m + 3\log n$
- D.
  $3\left( \log m + \frac{1}{2}\log n ight)$
Ta có: $m,n > 0$

$\log\left( m^{3}n^{2} ight) = \log m^{3} + \log n^{2} = 3\log m + 2\log n$
Câu 21: Vận dụng

Bà A gửi ngân hàng 100 triệu đồng vào ngân hàng với lãi suất 10%/ 1 năm theo hình thức lại kép một thời gian dài (nghĩa là nếu bà không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo). Năm nay gia đình có việc cần nên bà rút hết tiền trong ngân hàng để xử lí công việc. Sau khi rút cả vốn và lãi, bà trích ra 10 triệu để mua đồ tân gia cho con trai thì bà còn 240 triệu. Hỏi bà A đã gửi tiết kiệm được bao nhiêu năm? 10 năm||12 năm||20 năm||15 năm

Đáp án là:

Bà A gửi ngân hàng 100 triệu đồng vào ngân hàng với lãi suất 10%/ 1 năm theo hình thức lại kép một thời gian dài (nghĩa là nếu bà không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo). Năm nay gia đình có việc cần nên bà rút hết tiền trong ngân hàng để xử lí công việc. Sau khi rút cả vốn và lãi, bà trích ra 10 triệu để mua đồ tân gia cho con trai thì bà còn 240 triệu. Hỏi bà A đã gửi tiết kiệm được bao nhiêu năm? 10 năm||12 năm||20 năm||15 năm

Giả sử bà A đã gửi ngân hàng trong x năm

Số tiền bà nhận được là 250 triệu đồng

Áp dụng công thức lại kép thì sau n năm số tiền bà A nhận được là $T = 100.10^{6}.(1 + 0,1)^{n}$

$\Leftrightarrow 250.10^{6} = 100.10^{6}.(1 + 0,1)^{n}$

$\Leftrightarrow n = \log_{1,1}2,5\Leftrightarrow n \approx 9,61$

Vậy bà A đã gửi tiết kiệm trong 10 năm.
Câu 22: Nhận biết
Tìm hàm số đồng biến trên $\mathbb{R}$ trong các hàm số dưới đây?
- A.
  $y = \left( \frac{\pi}{2} ight)^{x}$
- B.
  $y = \left( 3 - \sqrt{5} ight)^{x}$
- C.
  $y = \left( \sqrt{3} - 1 ight)^{x}$
- D.
  $y = \left( \frac{e}{5} ight)^{x}$
Xét hàm số $y = \left( \frac{\pi}{2} ight)^{x}$ có $\frac{\pi}{2} > 1$ nên hàm số $y = \left( \frac{\pi}{2} ight)^{x}$ đồng biến trên $\mathbb{R}$ ?
Câu 23: Thông hiểu
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$ , $AC = a\sqrt{3}$ và $AA' = 3a$ . Chọn kết luận đúng về số đo góc giữa $A'C$ và $(ABC)$ ?
- A.
  $45^{0}$
- B.
  $90^{0}$
- C.
  $60^{0}$
- D.
  $30^{0}$
Hình vẽ minh họa

Ta có hình chiếu của A”C lên mặt phẳng (ABC) là AC

Suy ra $\left( A'C;(ABC) ight) = (A'C;AC) = \widehat{A'CA}$

Ta có: $\tan\widehat{A'CA} = \frac{AA'}{AC} = \frac{3a}{a\sqrt{3}} = \sqrt{3}$

$\Rightarrow \widehat{A'CA} = 60^{0} \Rightarrow \left( A'C;(ABC) ight) = 60^{0}$
Câu 24: Thông hiểu
Cho hai số thực dương a và b. Đơn giản biểu thức $E = \frac{a^{\frac{1}{3}}\sqrt{b} + b^{\frac{1}{3}}.\sqrt{a}}{\sqrt[6]{a} + \sqrt[6]{b}}$ ta được $E = a^{x}.b^{y}$ . Tích $x.y$ là:
- A.
  $x.y = \frac{1}{8}$
- B.
  $x.y = \frac{1}{21}$
- C.
  $x.y = \frac{1}{9}$
- D.
  $x.y = \frac{1}{18}$
Ta có:

$K = E = \frac{a^{\frac{1}{3}}\sqrt{b} + b^{\frac{1}{3}}.\sqrt{a}}{\sqrt[6]{a} + \sqrt[6]{b}} = \frac{a^{\frac{1}{3}}.b^{\frac{1}{2}} + b^{\frac{1}{3}}.a^{\frac{1}{2}}}{a^{\frac{1}{6}} + b^{\frac{1}{6}}}$

$= \frac{a^{\frac{1}{3}}.b^{\frac{1}{3}}\left( a^{\frac{1}{6}} + b^{\frac{1}{6}} ight)}{a^{\frac{1}{6}} + b^{\frac{1}{6}}} = a^{\frac{1}{3}}.b^{\frac{1}{3}}$

$\Rightarrow \left\{ \begin{matrix} x = \frac{1}{3} \\ y = \frac{1}{3} \\ \end{matrix} ight.\ \Rightarrow xy = \frac{1}{9}$
Câu 25: Nhận biết
Rút gọn biểu thức $W = b^{\frac{5}{3}}:\sqrt[3]{b}$ với $b > 0$ ta được:
- A.
  $W = b^{\frac{- 4}{3}}$
- B.
  $W = b^{\frac{4}{3}}$
- C.
  $W = b^{\frac{5}{9}}$
- D.
  $W = b^{2}$
Ta có:

$W = b^{\frac{5}{3}}:\sqrt[3]{b} = b^{\frac{5}{3}}:b^{\frac{1}{3}} = b^{\frac{5}{3} - \frac{1}{3}} = b^{\frac{4}{3}}$
Câu 26: Thông hiểu
Trong mặt phẳng (P) cho tam giác ABC, M là điểm không nằm trên (P) sao cho MA = MB = MC, d là đường thẳng đi qua M và vuông góc với (P). Khi đó đường thẳng d đi qua:
- A.
  Trực tâm của tam giác ABC.
- B.
  Trọng tâm của tam giác ABC.
- C.
  Tâm đường tròn ngoại tiếp tam giác ABC.
- D.
  Tâm đường đường tròn nội tiếp tam giác ABC.
Gọi H là giao điểm của đường thẳng d và mặt phẳng (P)
=> H là hình chiếu của M trên (P) nên từ MA = MB = MC
=> HA = HB = HC
=> Khi đó đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC.
Câu 27: Nhận biết
Cho $a > 0,n;m\mathbb{\in R}$ . Khẳng định nào sau đây đúng?
- A.
  $a^{m} + a^{n} = a^{m + n}$
- B.
  $a^{m}.a^{n} = a^{m - n}$
- C.
  $\left( a^{m} ight)^{n} = \left( a^{n} ight)^{m}$
- D.
  $\frac{a^{m}}{a^{n}} = a^{n - m}$
Theo tính chất lũy thừa ta có:

$\left( a^{m} ight)^{n} = \left( a^{n} ight)^{m}$
Câu 28: Thông hiểu
Một hộp dựng 10 viên bi xanh và 5 viên bi vàng. Có bao nhiêu cách lấy ngẫu nhiên 4 viên bi trong đó có ít nhất 2 viên bi màu xanh?
- A. 1050
- B. 1260
- C. 105
- D. 1200
Hộp chứa 10 + 5 = 15 viên bi
Số cách lấy 4 viên bi trong hộp là: $C_{15}^4 = 1365$ cách
Số cách lấy 4 viên bi không có viên bi xanh là: $C_5^4 = 5$ cách
Số cách lấy 4 viên bi có 1 viên bi xanh là: $C_{10}^1.C_5^3 = 100$ cách
=> Số lấy ngẫu nhiên 4 viên bi trong đó có ít nhất 2 viên bi màu xanh là: $1365 - 5 - 100 = 1260$ cách
Câu 29: Thông hiểu
Biết rằng $m,n$ là các số thực dương thỏa mãn $\dfrac{\log_{3}m.\log_{2}3}{1 + \log_{2}5} + \log n =1$ . Tìm khẳng định đúng trong các khẳng định sau?
- A.
  $m + n = 1$
- B.
  $m = 1 - n\log_{2}5$
- C.
  $mn = 10$
- D.
  $m\log_{2}5 + n = 1$
Ta có:

$\dfrac{\log_{3}m.\log_{2}3}{1 + \log_{2}5} + \log n =1$

$\Leftrightarrow\frac{\log_{2}m}{\log_{2}10} + \log n = 1$

$\Leftrightarrow \log m + \log n = 1 \Leftrightarrow \log(mn) = 1$

$\Leftrightarrow mn = 10$
Câu 30: Nhận biết
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác cân tại $A$ . Gọi $M$ là trung điểm cạnh $BC$ . Chọn kết luận đúng?
- A.
  $(B'C';AM) = 60^{0}$
- B.
  $(B'C';AM) = 30^{0}$
- C.
  $(B'C';AM) = 45^{0}$
- D.
  $(B'C';AM) = 90^{0}$
Hình vẽ minh họa

Vì tam giác ABC cân tại A và M là trung điểm của BC

=> $AM\bot BC$

Ta có: $BC//B'C'$

$\Rightarrow (B'C';AM) = (BC;AM) = 90^{0}$
Câu 31: Thông hiểu
Giáo viên trong lớp chuẩn bị 3 chiếc hộp:

Hộp 1 chứa 3 quả cầu đỏ và 5 quả cầu trắng.

Hộp 2 chứa 2 quả cầu đỏ và 2 quả cầu vàng.

Hộp 3 chứa 2 quả cầu đỏ và 3 quả cầu xanh.

Lấy ngẫu nhiên một hộp rồi lấy một quả cầu trong hộp đó. Gọi $X_{1}$ là biến cố lấy được hộp 1, $X_{2}$ là biến cố lấy được hộp 2, $X_{3}$ là biến cố lấy được hộp 3. Khi đó biến cố lấy ngẫu nhiên một hộp rồi lấy được một quả màu đỏ trong hộp đó biểu diễn như thế nào?
- A.
  $\left( X \cap X_{1} ight) \cap \left( X \cap X_{2} ight) \cap \left( X \cap X_{3} ight)$
- B.
  $X \cap X_{2} \cap X_{3}$
- C.
  $\left( X \cap X_{1} ight) \cup \left( X \cap X_{2} ight) \cup \left( X \cap X_{3} ight)$
- D.
  $X \cup X_{2} \cup X_{3}$
Lấy ngẫu nhiên một hộp trong hộp đó lấy ngẫu nhiên 1 quả cầu được quả màu đỏ thì hoặc là lấy được quả đỏ từ hộp 1 hoặc là lấy được quả đỏ từ hộp 2 hoặc lấy được quả đỏ từ hộp 3. Do đó ta biểu diễn biến cố cần tìm như sau:

$\left( X \cap X_{1} ight) \cup \left( X \cap X_{2} ight) \cup \left( X \cap X_{3} ight)$
Câu 32: Thông hiểu
Ta có: $4^{x} +4^{- x} = 14$ . Biểu thức $2^{x} +2^{- x}$ có giá trị là:
- A.
  $4$
- B.
  $16$
- C.
  $\sqrt{14}$
- D.
  $\pm 4$
Ta có:
$4^{x} + 4^{- x} = 14 \Leftrightarrow\left( 2^{x} + 2^{- x} ight)^{2} = 16$
$\Leftrightarrow \left\lbrack\begin{matrix}2^{x} + 2^{- x} = 4(tm) \\2^{x} + 2^{- x} = - 4(ktm) \\\end{matrix} ight.$
$\Rightarrow 2^{x} + 2^{- x} =4$
Câu 33: Vận dụng
Biết phương trình $8lo{g_{2}}^{2}\sqrt[3]{x} + 2(m - 1)log_{\frac{1}{4}}x - 2019 = 0$ có hai nghiệm phân biệt thỏa mãn $x_{1}x_{2} = 4$ . Chọn mệnh đề đúng.
- A.
  $m \in (1;2)$
- B.
  $m \in (2;5)$
- C.
  $m \in (0;1)$
- D.
  $m \in (4;7)$
Ta có:

$8\log{_{2}}^{2}\sqrt[3]{x} + 2(m -1)\log_{\frac{1}{4}}x - 2019 = 0$

$\Leftrightarrow\frac{8}{9}\log{_{2}}^{2}x - (m - 1)\log_{2}x - 2019 = 0$

Đặt $t = \log_{2}x \Leftrightarrow x =2^{t}$ ta được:

$\Leftrightarrow \frac{8}{9}t^{2} - (m - 1)t - 2019 = 0$

Phương trình đã cho có hai nghiệm phân biệt thỏa mãn $x_{1}x_{2} = 4$ khi và chỉ khi

$\frac{8}{9}t^{2} - (m - 1)t - 2019 = 0$ có hai nghiệm phân biệt thỏa mãn.

$2^{t_{1} + t_{2}} = 4 \Leftrightarrow t_{1} + t_{2} = 2$

$\Leftrightarrow \frac{9(m - 1)}{8} = 2 \Rightarrow m = \frac{25}{9} \in (2;5)$ .
Câu 34: Nhận biết
Tìm điều kiện xác định của hàm số $y =\log_{2}(x - 1)^{2}$ ?
- A.
  $x > 0$
- B.
  $x eq 1$
- C.
  $x\mathbb{\in R}$
- D.
  $x > 1$
Điều kiện xác định của hàm số $y =\log_{2}(x - 1)^{2}$ là:

$(x - 1)^{2} > 0 \Leftrightarrow x eq 1$
Câu 35: Thông hiểu
Giả sử $x_{1};x_{2}$ là hai nghiệm của phương trình $2^{x^{2} - x + 8} - 4^{1 - 3x} = 0$ . Xác định giá trị biểu thức $M = 4{x_{1}}^{2} - {x_{2}}^{2}$ biết $x_{1} > x_{2}$ ?
- A.
  $M = 7$
- B.
  $M = 32$
- C.
  $M = 40$
- D.
  $M = 11$
Ta có:

$2^{x^{2} - x + 8} - 4^{1 - 3x} = 0 \Leftrightarrow 2^{x^{2} - x + 8} = \left( 2^{2} ight)^{1 - 3x}$

$\Leftrightarrow 2^{x^{2} - x + 8} = 2^{2.(1 - 3x)}$

$\Leftrightarrow x^{2} - x + 8 = 2.(1 - 3x)$

$\Leftrightarrow x^{2} + 5x + 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x_{1} = - 2 \\ x_{2} = - 3 \\ \end{matrix} ight.\ (tm)$

$\Rightarrow M = 4{x_{1}}^{2} - {x_{2}}^{2} = 7$
Câu 36: Thông hiểu
Cho hình chóp tam giác $S.ABC$ có $SA = SB = SC = AB = a$ và $BC = a\sqrt{2}$ . Tính cosin góc giữa hai đường thẳng $AB$ và $SC$ .
- A.
  $\frac{\sqrt{2}}{2}$
- B.
  $\frac{1}{2}$
- C.
  $\frac{\sqrt{3}}{2}$
- D.
  $1$
Hình vẽ minh họa

Giả sử M, N, Q lần lượt là trung điểm các cạnh SA, SB, AC

Mặt khác ta có: $\left\{ \begin{matrix} MN//AB \\ MQ//SC \\ \end{matrix} ight.\ \Rightarrow (AB;SC) = (MN;MQ)$

Ta có: $AN = \frac{a\sqrt{3}}{2}$

$NC = \sqrt{\frac{SC^{2} + BC^{2}}{2} -\frac{SB^{2}}{4}}$ $= \sqrt{\dfrac{a^{2} + 2a^{2}}{2} - \dfrac{a^{2}}{4}} =\dfrac{a\sqrt{5}}{2}$

Xét tam giác NAC có:

$NQ = \sqrt{\frac{NA^{2} + CN^{2}}{2} -\frac{AC^{2}}{4}}$ $= \sqrt{\dfrac{\dfrac{3a^{2}}{4} + \dfrac{5a^{2}}{4}}{2}- \dfrac{a^{2}}{4}} = \dfrac{a\sqrt{3}}{2}$

Xét tam giác MNQ ta có:

$\cos\widehat{NMQ} = \frac{MN^{2} +MQ^{2} - NQ^{2}}{2MN.MQ}$ $= \dfrac{\dfrac{a^{2}}{4} + \dfrac{a^{2}}{4} -\dfrac{3a^{2}}{4}}{2.\dfrac{a}{2}.\dfrac{a}{2}} = -\dfrac{1}{2}$

$\Rightarrow \widehat{NMQ} = 120^{0} \Rightarrow (MN,MQ) = 180^{0} - 120^{0} = 60^{0}$

$\Rightarrow \cos(AB,SC) = \frac{1}{2}$
Câu 37: Nhận biết
Trong các kết quả dưới đây, kết quả nào là tập nghiệm của bất phương trình $\left( \frac{1}{3} ight)^{x} < 2$ ?
- A.
  $\left( \log_{2}\frac{1}{3}; + \inftyight)$
- B.
  $\left( \log_{\frac{1}{3}}2; + \inftyight)$
- C.
  $\left( - \infty;\log_{2}\frac{1}{3}ight)$
- D.
  $\left( - \infty;\log_{\frac{1}{3}}2ight)$
Ta có:

$\left( \frac{1}{3} ight)^{x} < 2 \Leftrightarrow x > log_{\frac{1}{3}}2$

Vậy tập nghiệm của bất phương trình đã cho là $x \in \left(\log_{\frac{1}{3}}2; + \inftyight)$
Câu 38: Nhận biết
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$ . Gọi $I;J$ lần lượt là trung điểm của các cạnh $SA$ và $SC$ .

Khẳng định nào sau đây đúng?
- A.
  $IJ\bot AB$
- B.
  $IJ\bot AD$
- C.
  $IJ\bot BD$
- D.
  $IJ\bot SD$
Vì IJ là đường trung bình của tam giác SAC nên $IJ//AC$

Ta có: $\left\{ \begin{matrix} IJ//AC \\ BD\bot AC \\ \end{matrix} ight.\ \Rightarrow BD\bot IJ$
Câu 39: Thông hiểu

Giả sử phương trình $\log_{\sqrt{3}}(x - 2) + \log_{3}(x - 4)^{2} =0$ có hai nghiệm $x_{1};x_{2}$ với $x_{1} > x_{2}$ . Khi đó giá trị của biểu thức $T = \left( x_{1} - x_{2} ight)^{2}=$ 2||9||-1||-7

Đáp án là:

Giả sử phương trình $\log_{\sqrt{3}}(x - 2) + \log_{3}(x - 4)^{2} =0$ có hai nghiệm $x_{1};x_{2}$ với $x_{1} > x_{2}$ . Khi đó giá trị của biểu thức $T = \left( x_{1} - x_{2} ight)^{2}=$ 2||9||-1||-7

Điều kiện xác định $\left\{ \begin{matrix}(x - 4)^{2} > 0 \\x - 2 > 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x eq 4 \\x > 2 \\\end{matrix} ight.$
Phương trình đã cho tương đương:
$\Leftrightarrow \log_{3^{\frac{1}{2}}}(x- 2) + 2\log_{3}|x - 4| = 0$
$\Leftrightarrow 2\log_{3}(x - 2) +2\log_{3}|x - 4| = 0$
$\Leftrightarrow \log_{3}\left\lbrack (x -2).|x - 4| ightbrack = \log_{3}1$
$\Leftrightarrow (x - 2).|x - 4| =1$
$\Leftrightarrow \left\lbrack\begin{matrix}\left\{ \begin{matrix}x \geq 4 \\(x - 2)(x - 4) = 1 \\\end{matrix} ight.\ \\\left\{ \begin{matrix}x < 4 \\(x - 2)(x - 4) = - 1 \\\end{matrix} ight.\ \\\end{matrix} ight.$
$\Leftrightarrow \left\lbrack\begin{matrix}\left\{ \begin{matrix}x \geq 4 \\x^{2} - 6x + 7 = 0 \\\end{matrix} ight.\ \\\left\{ \begin{matrix}x < 4 \\x^{2} - 6x + 9 = 0 \\\end{matrix} ight.\ \\\end{matrix} ight.$
$\Leftrightarrow \left\lbrack\begin{matrix}x_{1} = 3 + \sqrt{2} \\x_{2} = 3 \\\end{matrix} ight.\ \Rightarrow S = 2$
Câu 40: Thông hiểu
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = BC = a;AA' = a\sqrt{6}$ (như hình vẽ)

Gọi $\alpha$ là góc giữa đường thẳng $A'C$ và mặt phẳng đáy $(ABCD)$ . Khi đó:
- A.
  $\cos\alpha = \frac{1}{2}$
- B.
  $\cos\alpha = \frac{\sqrt{2}}{2}$
- C.
  $\cos\alpha = \frac{\sqrt{3}}{2}$
- D.
  $\cos\alpha = \frac{1}{\sqrt{3}}$
Hình vẽ minh họa

Ta có: $\left( A'C;(ABCD) ight) = (A'C;AC) = \widehat{A'CA} = \alpha$

Lại có: $AC = \sqrt{AB^{2} + BC^{2}} = a\sqrt{2}$

Xét tam giác $A'CA$ ta có:

$\Rightarrow \tan\alpha = \frac{AA}{AC} = \frac{a\sqrt{6}}{a\sqrt{2}} = \sqrt{3}$

$\Rightarrow \cos\alpha = \frac{1}{2}$

7 lượt xem

Sắp xếp theo

Xóa Gửi bình luận

Đề thi giữa HK2 Toán 11 Kết nối tri thức năm học 2023 – 2024 (Đề 5)

Chúc mừng Bạn đã hoàn thành bài!