Cho hai biểu đồ chấm như hình dưới của mẫu A và mẫu B.

Chọn kết luận đúng.
Khoảng biến thiên của mẫu A và mẫu B đều là .
Vậy hai mẫu số liệu có khoảng biến thiên như nhau.
Cho hai biểu đồ chấm như hình dưới của mẫu A và mẫu B.

Chọn kết luận đúng.
Khoảng biến thiên của mẫu A và mẫu B đều là .
Vậy hai mẫu số liệu có khoảng biến thiên như nhau.
Trong mặt phẳng tọa độ ![]() , cho hai vecto
, cho hai vecto ![]() và
và ![]() . Tính
. Tính ![]() ?
?
Theo bài ra ta có:
và
Khi đó:
Tìm giá trị bất thường của mẫu số liệu: 8 50 6 4 2
Sắp xếp mẫu theo thứ tự không giảm: 2 4 6 8 50
Số liệu chính giữa là 6 nên .
Trung vị của mẫu số liệu 2 4 là .
Trung vị của mẫu số liệu 8 50 là .
Khoảng tứ phân vị là .
Ta có: .
Ta có: .
Không có giá trị nào trong mẫu nhỏ hơn -36 và lớn hơn 68. Vậy mẫu không có giá trị bất thường.
Trong hộp có 5 quả cầu đỏ và 7 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 4 quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh.
Trường hợp 1: 4 quả đỏ + 0 quả xanh
Chọn 4 quả đỏ từ 5 quả đỏ có: (cách).
Trường hợp 2: 3 quả đỏ + 1 quả xanh
Chọn 3 quả đỏ từ 5 quả đỏ, 1 quả xanh từ 7 quả xanh có: (cách).
Vậy có (cách).
Có 3 bạn nam và 4 bạn nữ. Hỏi có bao nhiêu cách xếp 7 bạn vào 1 dãy ghế hàng ngang liền nhau gồm 7 chỗ ngồi?
Xếp 7 bạn vào dãy 7 ghế: có 7! (cách).
Phương sai của một mẫu số liệu ![]() bằng
bằng
Phương sai của một mẫu số liệu bằng bình phương của độ lệch chuẩn.
Cho tập hợp ![]() . Có thể lập được bao nhiêu số tự nhiên chẵn có 4 chữ số đôi một khác nhau từ các chữ số thuộc tập hợp
. Có thể lập được bao nhiêu số tự nhiên chẵn có 4 chữ số đôi một khác nhau từ các chữ số thuộc tập hợp ![]() ?
?
Gọi số tự nhiên có bốn chữ số là:
TH1: d = 0 => d có 1 cách.
Số cách chọn a, b, c lần lượt là 5, 4, 3
=> Số các số tạo thành là: 1.5.4.3 = 60 (số)
TH2: => Chữ số d có 2 cách chọn.
=> Chữ số a có 4 cách.
=> Số cách chọn b, c lần lượt là 4, 3 cách.
=> Số các số tạo thành là: 2.4.4.3 = 96 (số)
Vậy có tất cả 60 + 96 = 156 (số) thỏa mãn yêu cầu đề bài.
Cho số gần đúng của ![]() là
là ![]() . Sai số tuyệt đối của số gần đúng này là:
. Sai số tuyệt đối của số gần đúng này là:
Sai số tuyệt đối là:
Độ lệch chuẩn là gì?
Độ lệch chuẩn là căn bậc hai của phương sai.
Mỗi khi thực hiện giao dịch qua app thanh toán tiền, ngân hàng sẽ gửi một mã xác thực (OTP – One Time Password) gồm 6 chữ số từ 0 đến 9. Hỏi có thể có bao nhiêu mã OTP?
Mỗi mã xác thực gồm 6 chữ số được tạo thành từ các số từ 0 đến 9
=> Với mỗi chữ số trong mã xác thực sẽ có 10 cách chọn
=> Số mã xác thực có thể tạo thành là: mã.
Cho đa giác đều gồm ![]() đỉnh với
đỉnh với ![]() . Số tam giác tạo thành từ 3 đỉnh của đa giác nhưng không có cạnh nào trùng với cạnh của đa giác gấp 5 lần số tam giác tạo thành từ 3 đỉnh của đa giác nhưng có đúng 1 cạnh trùng với 1 cạnh của đa giác. Hỏi đa giác có bao nhiêu đỉnh?
. Số tam giác tạo thành từ 3 đỉnh của đa giác nhưng không có cạnh nào trùng với cạnh của đa giác gấp 5 lần số tam giác tạo thành từ 3 đỉnh của đa giác nhưng có đúng 1 cạnh trùng với 1 cạnh của đa giác. Hỏi đa giác có bao nhiêu đỉnh?
Số tam giác tạo thành từ 3 đỉnh của đa giác là (tam giác)
Số tam giác tạo thành có đúng hai cạnh trùng với hai cạnh của đa giác là n (tam giác).
Số tam giác tạo thành có đúng một cạnh là cạnh của đa giác là:
Số tam giác tạo thành không có cạnh nào là cạnh của đa giác là:
Theo giả thiết ta có:
Vậy đa giác có 35 đỉnh.
Cho giá trị gần đúng của ![]() là
là ![]() . Sai số tuyệt đối của số
. Sai số tuyệt đối của số ![]() không vượt quá giá trị nào sau đây?
không vượt quá giá trị nào sau đây?
Sai số tuyệt đối của số là:
Suy ra sai số tuyệt đối của số không vượt quá
.
Trong mặt phẳng tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() có phương trình
có phương trình ![]() . Hãy chỉ ra một vectơ pháp tuyến của đường thẳng đã cho?
. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng đã cho?
Một vectơ pháp tuyến của đường thẳng là:
.
Cho hình vuông ![]() , tính
, tính ![]() .
.
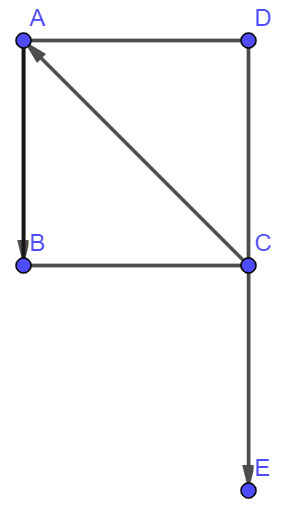
Vẽ .
Ta có: .
Cho dãy số liệu thống kê ![]() . Tìm số nguyên dương
. Tìm số nguyên dương ![]() , biết số trung bình cộng của dãy số liệu thống kê đó bằng
, biết số trung bình cộng của dãy số liệu thống kê đó bằng ![]() .
.
Điểm trung bình cộng của dãy số trên là
Vậy thỏa mãn yêu cầu bài toán.
Trong mặt phẳng tọa độ ![]() ,cho tam giác
,cho tam giác ![]() có tọa độ các điểm
có tọa độ các điểm ![]() . Đường thẳng
. Đường thẳng ![]() đi qua
đi qua ![]() và song song với
và song song với ![]() có phương trình tổng quát là:
có phương trình tổng quát là:
Ta có:
Phương trình tổng quát AC là:
Đường thẳng song song với
nên d có dạng
Do điểm
Vậy .
Cho dãy số liệu ![]() . Kết luận nào dưới đây đúng?
. Kết luận nào dưới đây đúng?
Sắp xếp dãy số liệu theo thứ tự không tăng như sau:
Khi đó:
Vậy kết luận đúng là: .
Trong mặt phẳng tọa độ ![]() , cho tam giác
, cho tam giác ![]() biết
biết ![]() . Tính độ dài đường trung tuyến kẻ từ đỉnh
. Tính độ dài đường trung tuyến kẻ từ đỉnh ![]() của tam giác
của tam giác ![]() ?
?
Gọi M là trung điểm của BC
Khi đó tọa độ của M là:
Suy ra độ dài đường trung tuyến kẻ từ đỉnh A hay độ dài đoạn AM là:
Vậy độ dài đường trung tuyến kẻ từ đỉnh A của tam giác ABC là .
Cho tam giác ![]() ,
, ![]() . Tính tọa độ điểm
. Tính tọa độ điểm ![]() là chân đường phân giác góc
là chân đường phân giác góc ![]() . Biết
. Biết ![]() .
.
Theo tính chất đường phân giác: . Suy ra
.
Gọi . Suy ra
.
Ta có:
Vậy tọa độ điểm .
Trong mặt phẳng hệ trục tọa độ ![]() cho các tọa độ các điểm
cho các tọa độ các điểm ![]() và
và ![]() . Xác định tọa độ điểm
. Xác định tọa độ điểm ![]() sao cho
sao cho ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() ?
?
Xét tam giác ABD có G là trọng tâm khi đó ta có:
Vậy tọa độ điểm .
Cho tập hợp M = {a; b; c}. Số hoán vị của ba phần tử của M là:
Số hoán vị của ba phần tử của M là: 3! = 6.
Xác định số trung vị của dãy số liệu ![]() ?
?
Dãy số đã cho được sắp xếp theo thứ tự không giảm.
Dãy số có 7 số liệu nên số trung vị đứng giữa dãy số.
Do đó số trung vị của dãy trên là 7.
Kết quả đi chiều dài của một cây thước là ![]() thì sai số tương đối của phép đo là:
thì sai số tương đối của phép đo là:
Ta có:
Tìm hệ số của ![]() trong khai triển nhị thức Newton của
trong khai triển nhị thức Newton của ![]() ?
?
Số hạng tổng quát là:
Hệ số của tìm được khi
Vậy hệ số của trong khai triển là
.
Xác định số hạng không chứa x trong khai triển nhị thức Newton ![]() . Biết rằng
. Biết rằng ![]() .
.
Ta có:
Xét khai triển
Số hạng tổng quát
Số hạng không chứa x ứng với
Suy ra số hạng không chứa x là .
Trong balo của học sinh A có 8 bút chì khác, 6 bút bi và 10 quyển vở. Số cách chọn một đồ vật trong balo là:
Áp dụng quy tắc cộng, số cách chọn một đồ vật trong balo là: 8 + 6 + 10 = 24 cách.
Tính tổng các hệ số các đơn thức trong khai triển nhị thức Newton ![]() ?
?
Để có tổng các hệ số ta thay ta được:
Trong các phương trình sau đây, phương trình nào là phương trình tham số của đường thẳng?
Phương trình tham số của đường thẳng là:
Giá của một số bó hoa (đơn vị: nghìn đồng) trong cửa hàng được thống kê như sau: ![]() . Mốt của mẫu số liệu này là:
. Mốt của mẫu số liệu này là:
Bó hoa có giá 300 nghìn đồng có tần số lớn nhất nên suy ra .
Trên giá sách có 8 quyển tiểu thuyết khác nhau và 6 quyển truyện tranh khác nhau. Số cách chọn một trong các quyển sách đó là:
Số cách chọn một trong các quyển sách đó là: 8 + 6 = 14 cách.
Trong các vecto dưới đây, vecto nào cùng phương với vecto ![]() ?
?
Nhận thấy nên
cùng phương với
.
Trong mặt phẳng tọa độ ![]() cho
cho ![]() . Xác định tọa độ trọng tâm
. Xác định tọa độ trọng tâm ![]() của tam giác
của tam giác ![]() ?
?
Vì H là trọng tâm tam giác OPQ nên ta có:
Vậy trọng tâm tam giác cần tìm là .
Cho ba nhóm học sinh:
Nhóm 1 gồm 6 học sinh có cân nặng trung bình là 45kg.
Nhóm 2 gồm 11 học sinh có cân nặng trung bình là 50kg.
Nhóm 3 gồm 8 học sinh có cân nặng trung bình là 42kg.
Hãy tính khối lượng trung bình của cả ba nhóm học sinh trên?
Tổng khối lượng của mỗi nhóm lần lượt là:
Khối lượng trung bình của cả ba nhóm là:
Vậy khối lượng trung bình của cả ba nhóm học sinh là .
Trong mặt phẳng tọa độ ![]() , cho hình chữ nhật
, cho hình chữ nhật ![]() . Gọi
. Gọi ![]() là hình chiếu của điểm
là hình chiếu của điểm ![]() trên cạnh
trên cạnh ![]() , điểm
, điểm ![]() là trung điểm của
là trung điểm của ![]() . Viết phương trình tổng quát đường thẳng
. Viết phương trình tổng quát đường thẳng ![]() , biết rằng tọa độ điểm
, biết rằng tọa độ điểm ![]() , đường chéo
, đường chéo ![]() có phương trình
có phương trình ![]() và tọa độ điểm
và tọa độ điểm ![]() ?
?
Hình vẽ minh họa
Ta có: có một vecto pháp tuyến
nên AH nhận
làm một vecto chỉ phương.
Do đó đường thẳng có phương trình tham số là
H là giao điểm của AH và BD nên tọa độ của H thỏa mãn hệ phương trình:
Ta có: mà I là trung điểm của BH nên suy ra
Đường thẳng đi qua điểm nhận
làm một vecto pháp tuyến có phương trình tổng quát là
Cho tam giác ![]() . Tập hợp các điểm
. Tập hợp các điểm ![]() thỏa mãn
thỏa mãn ![]() là:
là:
Vì , mà
cố định nên suy ra tập hợp
là đường thẳng đi qua
và vuông góc với
.
Gọi ![]() là tập hợp tất cả các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ các chữ số
là tập hợp tất cả các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ các chữ số ![]() Tính tổng tất cả các số thuộc tập
Tính tổng tất cả các số thuộc tập ![]()
Số các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ là
số.
Vì vai trò các chữ số như nhau nên mỗi chữ số xuất hiện ở hàng đơn vị là
lần.
Tổng các chữ số ở hàng đơn vị là .
Tương tự thì mỗi lần xuất hiện ở các hàng chục, trăm, nghìn, chục nghìn của mỗi chữ số là 24 lần.
Vậy tổng các số thuộc tập là
.
Tìm hệ số của ![]() trong khai triển nhị thức Newton
trong khai triển nhị thức Newton ![]() với
với ![]() , biết
, biết ![]() là số tự nhiên lớn nhất thỏa mãn
là số tự nhiên lớn nhất thỏa mãn ![]() .
.
Điều kiện:
Khi đó
.
Số hạng tổng quát trong khai triển là
.
Tìm sao cho
.
Vậy hệ số của số hạng chứa là
.
Số quy tròn của số gần đúng ![]() với
với ![]() là:
là:
Quy tròn đến hàng trăm nên số quy tròn của số gần đúng
là:
.
Nhà sản xuất công bố chiều dài và chiều rộng của 1 tấm ván hình chữ nhật lần lượt là ![]() và
và ![]() (đơn vị: cm). Tính diện tích của tấm thép.
(đơn vị: cm). Tính diện tích của tấm thép.
Gọi và
lần lượt là chiều dài và chiều rộng thực của tấm thép.
Ta có: và
.
Suy ra: .
Do đó:
Vậy diện tích tấm thép là .
Trong mặt phẳng tọa độ ![]() , cho tọa độ hai điểm
, cho tọa độ hai điểm ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() đối xứng với điểm
đối xứng với điểm ![]() qua
qua ![]() ?
?
Gọi tọa độ điểm C là
Vì điểm đối xứng với điểm
qua
suy ra
là trung điểm của
Vậy tọa độ điểm C cần tìm là .
