Biết hệ số của ![]() trong khai triển nhị thức Newton của
trong khai triển nhị thức Newton của ![]() là
là ![]() . Xác định giá trị
. Xác định giá trị ![]() ?
?
Số hạng thứ trong khai triển
là:
với
và
Số hạng chứa ứng với
Ta có:
Vậy .
Biết hệ số của ![]() trong khai triển nhị thức Newton của
trong khai triển nhị thức Newton của ![]() là
là ![]() . Xác định giá trị
. Xác định giá trị ![]() ?
?
Số hạng thứ trong khai triển
là:
với
và
Số hạng chứa ứng với
Ta có:
Vậy .
Tính giá trị ![]() biết rằng
biết rằng ![]() ?
?
Ta có:
Tích các nghiệm của phương trình ![]() là:
là:
Điều kiên:
Phương trình tương đương:
Đặt
Với t = 4 ta có:
Tìm tập xác định của hàm số ![]() ?
?
Điều kiện xác định:
.
Vậy tập xác định của hàm số là .
Số nghiệm của phương trình ![]() là
là
Điều kiện: .
⇔
⇔
⇔ ⇔ x = 0(TM).
Vậy, phương trình có một nghiệm.
Trong mặt phẳng tọa độ ![]() , tọa độ vecto
, tọa độ vecto ![]() là:
là:
Ta có: .
Cho biểu thức ![]() , khi khai triển nhị thức đã cho ta được bao nhiêu số hạng?
, khi khai triển nhị thức đã cho ta được bao nhiêu số hạng?
Trong khai triển nhị thức Newton có
số hạng.
Có ![]() viên bi đen khác nhau,
viên bi đen khác nhau, ![]() viên bi đỏ khác nhau,
viên bi đỏ khác nhau, ![]() viên bi xanh khác nhau. Hỏi có bao nhiêu cách xếp các viên bi trên thành dãy sao cho các viên bi cùng màu ở cạnh nhau?
viên bi xanh khác nhau. Hỏi có bao nhiêu cách xếp các viên bi trên thành dãy sao cho các viên bi cùng màu ở cạnh nhau?
Số cách xếp viên bi đen khác nhau thành một dãy bằng.
.
Số cách xếp viên bi đỏ khác nhau thành một dãy bằng.
.
Số cách xếp viên bi đen khác nhau thành một dãy bằng.
.
Số cách xếp nhóm bi thành một dãy bằng.
.
Vậy số cách xếp thỏa yêu cầu đề bài bằng cách.
Tính giá trị biểu thức: ![]() .
.
Xét khai triển
Thay ta được:
Trong mặt phẳng tọa độ ![]() cho hai vecto
cho hai vecto ![]() . Khi nào hai vecto
. Khi nào hai vecto ![]() và
và ![]() bằng nhau?
bằng nhau?
Ta có:
Vậy hai vecto và
bằng nhau khi
.
Trong mặt phẳng tọa độ ![]() , gọi
, gọi ![]() là trực tâm tam giác
là trực tâm tam giác ![]() có tọa độ các đỉnh
có tọa độ các đỉnh ![]() và
và ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Gọi . Vì I là trọng tâm tam giác ABC nên ta có hệ phương trình:
Ta có: là trực tâm tam giác ABC nên
Ta có hệ phương trình
Vậy biểu thức
Tính góc giữa hai đường thẳng ![]() và
và ![]()
Ta có:
Vectơ pháp tuyến của hai đường thẳng lần lượt là
Suy ra
Suy ra
Trong các phương trình sau đây, phương trình nào là phương trình tham số của đường thẳng?
Phương trình tham số của đường thẳng là:
Ngân hàng câu hỏi kiểm tra Toán lớp 11A gồm 35 câu hỏi đại số và 15 câu hỏi hình học. Học sinh được chọn một câu hỏi để trả lời. Khi đó số khả năng có thể xảy ra bằng:
Áp dụng quy tắc cộng ta có số khả năng có thể xảy ra là: 35 + 15 = 50 khả năng.
Có thể lập được bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau từ tập hợp ![]() và không vượt quá
và không vượt quá ![]() ?
?
TH1: Số cần tìm có dạng
Chữ số d có 7 cách chọn là một trong các chữ số .
Suy ra có 7 số thỏa mãn.
TH2: Số cần tìm có dạng
3 vị trí còn lại có cách chọn
Suy ra có 504 số thỏa mãn
Kết hợp cả hai trường hợp ta có: 504 + 7 = 511 số được tạo thành thỏa mãn yêu cầu đề bài.
Xác định vị trí tương đối của hai đường thẳng ![]() và
và ![]() ?
?
Ta có: suy ra hai đường thẳng (d) và (d’) song song với nhau.
Cho tập hợp ![]() có 10 phần tử. Hỏi có bao nhiêu tập con có 8 phần tử của tập hợp
có 10 phần tử. Hỏi có bao nhiêu tập con có 8 phần tử của tập hợp ![]() ?
?
Mỗi tập con có 8 phần tử của tập hợp là một tổ hợp chập 8 của 10. Vậy số tập con có 8 phần tử của tập hợp
là.
.
Số nghiệm thực của phương trình ![]() là
là
ĐK: ,
.
Giả sử phương trình đường thẳng ![]() với
với ![]() và
và ![]() là phân số tối giản. Biết rằng đường thẳng
là phân số tối giản. Biết rằng đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và cách điểm
và cách điểm ![]() một khoảng bằng
một khoảng bằng ![]() . Khi đó giá trị biểu thức
. Khi đó giá trị biểu thức ![]() là:
là:
Ta có:
Với thì
(loại do
)
Xét thì
Với thì ta chọn
Vậy
Trong mặt phẳng tọa độ ![]() , mỗi đường thẳng có bao nhiêu vectơ pháp tuyến?
, mỗi đường thẳng có bao nhiêu vectơ pháp tuyến?
Một đường thẳng có vô số vectơ pháp tuyến và chúng có cùng phương với nhau.
Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao chữ số đầu chẵn chữ số đứng cuối lẻ.
Vì chữ số đứng đầu chẵn nên có
cách chọn, chữ số đứng cuối lẻ nên
có 4 cách chọn. Các số còn lại có
cách chọn
Vậy có số thỏa yêu cầu bài toán.
Cho tam giác ![]() có tọa độ ba đỉnh
có tọa độ ba đỉnh ![]() . Trọng tâm G của tam giác
. Trọng tâm G của tam giác ![]() là:
là:
Vì G là trọng tâm tam giác ABC nên tọa độ G là nghiệm hệ phương trình:
Xác định m để biểu thức ![]() là tam thức bậc hai.
là tam thức bậc hai.
Để biểu thức là tam thức bậc hai ta có:
Tập nghiệm của bất ![]() là:
là:
Ta có: .
Vậy
Các giá trị của tham số m để phương trình ![]() (1) có nghiệm là:
(1) có nghiệm là:
Đặt
⇒ t2 = x2 − x + 1 ⇒ (2x−1)2 = 4x2 − 4x + 1 = 4t2 − 3
Vì nên
Phương trình (1) trở thành 4t2 − 3 + m = t ⇔ − 4t2 + t + 3 = m.
Xét hàm số y = − 4t2 + t − 3 với
Ta có
Bảng biến thiên
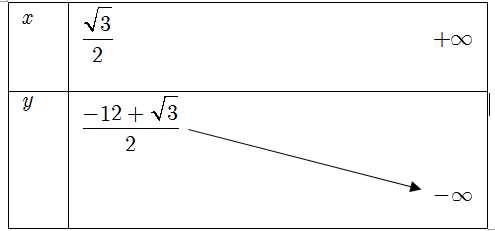
Phương trình (1) có nghiệm ⇔ phương trình có nghiệm
⇔ đồ thị hàm số y = − 4t2 + t − 3 trên cắt đường thẳng
.
Vậy phương trình (1) có nghiệm khi và chỉ khi .
Cho hai vectơ ![]() và
và ![]() khác
khác ![]() . Xác định góc
. Xác định góc ![]() giữa hai vectơ
giữa hai vectơ ![]() và
và ![]() khi
khi ![]() .
.
Ta có .
Mà theo giả thiết
Suy ra
Cho tam giác ![]() có tọa độ ba đỉnh
có tọa độ ba đỉnh ![]() . Xác định tọa độ điểm
. Xác định tọa độ điểm ![]() thỏa mãn
thỏa mãn ![]() ?
?
Giả sử tọa độ điểm D là:
Ta có: thỏa mãn
Ta có:
Có thể lập được bao nhiêu số tự nhiên có 4 chữ số từ tập hợp các chữ số ![]() ?
?
Gọi số tự nhiên có 4 chữ số là: .
Mỗi chữ số có 6 cách chọn.
Mà số cần lập gồm 4 chữ số nên theo quy tắc nhân có thể lập được số.
Tìm m để f(x) = x2 − 2(2m−3)x + 4m − 3 > 0, ∀x ∈ ℝ?
f(x) = x2 − 2(2m−3)x + 4m − 3 > 0, ∀x ∈ ℝ⇔Δ < 0 ⇔ 4m2 − 16m + 12 < 0 ⇔ 1 < m < 3.
Cho hai điểm ![]() . Đường thẳng nào sau đây cách đều hai điểm
. Đường thẳng nào sau đây cách đều hai điểm ![]() ?
?
Gọi đường thẳng cần tìm là đường thẳng d.
Khi đó đường thẳng d cách đều hai điểm C và D khi:
TH1: Đường thẳng đó song song hoặc trùng với đường thẳng CD,
Ta có: nên một vectơ pháp tuyến của CD là
Vậy trong các đường thẳng đã cho chỉ có đường thẳng .
TH2: d là đường trung trực của CD.
Khi đó d đi qua trung điểm của CD và nhận
làm VTPT.
Suy ra phương trình đường thẳng d là:
Vậy đáp án là
Một chiếc hộp chứ 5 quả cầu trắng và 6 quả cầu đỏ. Lấy ngẫu nhiên đồng thời ba quả trong hộp, biết rằng các quả cầu có kích thước và khối lượng như nhau. Hỏi có bao nhiêu cách lấy được đồng thời 3 quả cầu sao cho 3 quả cầu lấy ra có ít nhất một quả cầu trắng?
Trường hợp 1: 1 quả trắng và 2 quả đỏ.
Số cách lấy là
Trường hợp 2: 2 quả trắng và 1 quả đỏ.
Số cách lấy là
Trường hợp 3: 3 quả trắng.
Số cách lấy là
Do vậy số cách lấy ngẫu nhiên 3 quả cầy trong hộp sao cho trong 3 quả cầu lấy ra có ít nhất 1 quả cầu trắng là: 75 + 60 + 10 = 145 (cách)
Tìm giá trị thực của m để phương trình |2x2−3x+2| = 5m − 8x − 2x2 có nghiệm duy nhất.
Ta thấy 2x2 − 3x + 2 > 0, ∀x ∈ ℝ nên |2x2−3x+2| = 2x2 − 3x + 2.
Do đó phương trình đã cho tương đương với 4x2 + 5x + 2 − 5m = 0. (*)
Khi đó để phương trình đã cho có nghiệm duy nhất khi và chỉ khi (*) có nghiệm duy nhất .
Cho các tam thức f(x) = 2x2 − 3x + 4; g(x) = − x2 + 3x − 4; h(x) = 4 − 3x2. Số tam thức đổi dấu trên ℝ là:
Tam thức đổi dấu khi tam thức có 2 nghiệm phân biệt hay Δ > 0.Vậy chỉ có h(x) = 4 − 3x2 có 2 nghiệm.
Trong mặt phẳng ![]() , cho tam giác
, cho tam giác ![]() có tọa độ các điểm
có tọa độ các điểm ![]() . Gọi
. Gọi ![]() là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác ![]() . Xác định giá trị biểu thức
. Xác định giá trị biểu thức ![]() ?
?
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IA = IB = IC
Ta có:
Từ đó ta suy ra hệ phương trình:
Cho f(x) = x2 − 4x + 3. Trong các mệnh đề sau, mệnh đề đúng là:
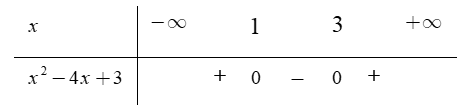
Dựa vào bảng xét dấu thì f(x) ≤ 0, ∀x ∈ [ 1; 3 ].
Cho tam giác đều ![]() có cạnh bằng
có cạnh bằng ![]() Tính tích vô hướng
Tính tích vô hướng ![]()
.
Cho tọa độ ba điểm ![]() . Tính
. Tính ![]() ?
?
Ta có:
Trong mặt phẳng tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() và tọa độ một điểm
và tọa độ một điểm ![]() . Ta kí hiệu khoảng cách từ điểm
. Ta kí hiệu khoảng cách từ điểm ![]() đến đường thẳng
đến đường thẳng ![]() là
là ![]() . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
Khoảng cách từ điểm A đến đường thẳng được tính bởi công thức:
Vậy kết luận đúng là: “”.
Biết rằng ![]() thỏa mãn biểu thức
thỏa mãn biểu thức ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có:
Lại có:
Trong mặt phẳng tọa độ ![]() , cho tam giác
, cho tam giác ![]() có
có ![]() . Phương trình tổng quát của đường trung tuyến kẻ từ đỉnh
. Phương trình tổng quát của đường trung tuyến kẻ từ đỉnh ![]() của tam giác
của tam giác ![]() là:
là:
Gọi I là trung điểm của AC. Ta có:
Đường trung tuyến BI đi qua điểm B và nhận làm vectơ chỉ phương nên có vectơ pháp tuyến
.
Phương trình tổng quát của đường thẳng là:
