Diện tích hình phẳng được gạch chéo trong hình bên bằng

Dựa và hình vẽ ta có diện tích hình phẳng được gạch chéo trong hình bên là:
Diện tích hình phẳng được gạch chéo trong hình bên bằng

Dựa và hình vẽ ta có diện tích hình phẳng được gạch chéo trong hình bên là:
Cho hàm số ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên khoảng
trên khoảng ![]() . Giá trị biểu thức
. Giá trị biểu thức ![]() bằng:
bằng:
Ta có:
Theo bài ra ta có:
Nguyên hàm của hàm số ![]() là:
là:
Ta có:
.
Cho F(x) là một nguyên hàm của hàm số ![]() . Hàm số
. Hàm số ![]() có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
=> có 5 nghiệm đơn
=> Hàm số có 5 điểm cực trị
Cho hàm số ![]() xác định trên
xác định trên ![]() thỏa mãn
thỏa mãn ![]() ;
; ![]() . Tính
. Tính ![]() ?
?
Trên khoảng ta có:
Mà
Trên khoảng ta có:
Mà
Vậy
.
Trong không gian với hệ tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() và
và ![]() với
với ![]() là tham số thực. Tổng các giá trị của m để
là tham số thực. Tổng các giá trị của m để ![]() và
và ![]() vuông góc nhau bằng bao nhiêu?
vuông góc nhau bằng bao nhiêu?
Ta có:
có vectơ pháp tuyến
có véc-tơ pháp tuyến
(P) và (Q) vuông góc với nhau khi và chỉ khi
Điều này tương đương với
.
Cho hai vectơ ![]() Xác định vectơ
Xác định vectơ ![]() , biết
, biết ![]() cùng phương với
cùng phương với ![]() và
và ![]()
Gọi tọa độ của là
Theo đề bài, ta có cùng phương
Mặt khác, , thay vào ta được:
Viết công thức tính thể tích ![]() của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số ![]() , trục
, trục ![]() và hai đường thẳng
và hai đường thẳng ![]() xung quanh trục
xung quanh trục ![]() .
.
Thể tích của khối tròn xoay cần tính là:
Hàm số nào sau đây là một nguyên hàm của hàm số ![]() ?
?
Vì:
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:
Gọi bán kính đáy là R.
Hình trụ có chu vi đáy bằng 2a nên ta có .
Suy ra hình trụ này có đường cao .
Vậy thể tích khối trụ (đvtt).
Trong không gian hệ trục tọa độ ![]() , cho tam giác
, cho tam giác ![]() có tọa các điểm
có tọa các điểm ![]() . Tính số đo góc
. Tính số đo góc ![]() ?
?
Ta có:
Tích phân  có giá trị là:
có giá trị là:
Tích phân có giá trị là:
Ngoài ra ta có thể kiểm tra bằng máy tính, dễ dàng thu được kết quả như cách trên.
Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:
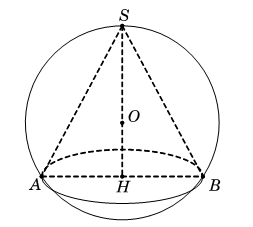
Hình vẽ kết hợp với giả thiết, ta có
Suy ra và
Thể tích khối nón (đvtt).
Thể tích khối cầu (đvtt).
Suy ra
Trong không gian với hệ tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() . Xác định
. Xác định ![]() để hai mặt phẳng
để hai mặt phẳng ![]() và
và ![]() song song với nhau?
song song với nhau?
Hai mặt phẳng đã cho song song với nhau khi và chỉ khi
Tập xác định
Vậy thì hai mặt phẳng
song song với nhau.
Tính diện tích hình phẳng giới hạn bởi các đường thẳng ![]() ?
?
Hình vẽ minh họa
Ta có:
Từ đó ta thấy phương trình hoành độ không có nghiệm nào thuộc khoảng
Diện tích hình giới hạn là
Cho hàm số f(x) xác định trên ![]() thỏa mãn
thỏa mãn ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức ![]()
=>
Theo bài ra ta có:
=>
=>
Tìm họ nguyên hàm của hàm số ![]() ?
?
Ta có:
Tính tích phân ![]() ?
?
Ta có:
Trong không gian với hệ tọa độ ![]() , cho ba điểm
, cho ba điểm ![]() và mặt phẳng
và mặt phẳng ![]() . Điểm
. Điểm ![]() nằm trên mặt phẳng
nằm trên mặt phẳng ![]() thỏa mãn
thỏa mãn ![]() . Tính
. Tính ![]() ?
?
Ta có
Với , ta có
Với , ta có
Từ (1); (2); (3) ta có hệ phương trình:
Trong không gian ![]() , cho tọa độ các vectơ
, cho tọa độ các vectơ ![]() ;
; ![]() và
và ![]() . Mệnh đề nào sau đây sai?
. Mệnh đề nào sau đây sai?
Ta có: suy ra “
” là mệnh đề sai.
Trong không gian tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() và
và ![]() . Tìm
. Tìm ![]() để
để ![]() vuông góc với
vuông góc với ![]() ?
?
Ta có: (P) vuông góc với (Q) khi và chỉ khi các vectơ pháp tuyến của chúng vuông góc với nhau, tức là .
Tìm nguyên hàm của hàm số ![]() ?
?
Ta có:
Trong không gian ![]() , tính khoảng cách từ điểm
, tính khoảng cách từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]() ?
?
Khoảng cách từ điểm đến mặt phẳng
là:
Tìm nguyên hàm của hàm số ![]()
Cho giá trị của tích phân  ,
,  . Giá trị của a + b là:
. Giá trị của a + b là:
Ta có:
Ngoài ra ta có thể sử dụng máy tính cầm tay nhập trực tiếp biểu thức và tính ra kết quả.
Gọi ![]() là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có:
Cho F(x) là một nguyên hàm của hàm số ![]() thỏa mãn
thỏa mãn ![]() . Tìm F(x)
. Tìm F(x)
Mặt khác
=>
Cho tích phân  , a và b là các số hữu tỉ. Giá trị của
, a và b là các số hữu tỉ. Giá trị của ![]() là:
là:
Ta có:
, với
Trong không gian Oxyz cho hai vectơ![]() khác
khác ![]() cùng phương. Câu nào sau đây sai? (có thể chọn 2 đáp án)
cùng phương. Câu nào sau đây sai? (có thể chọn 2 đáp án)
Ta xét đáp án : sai vì thiếu điều kiện
.
Xét đáp án : luôn đúng vì 2 vecto cùng phương với nhau.
Ta xét tiếp: : cũng sai, vì thiếu điều kiện
Như vậy ta sẽ chọn 2 đáp án có 2 ý sai.
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Điểm đối xứng với
. Điểm đối xứng với ![]() qua mặt phẳng
qua mặt phẳng ![]() có tọa độ là:
có tọa độ là:
Giữ nguyên y, z và đổi dấu x nên ta suy ra điểm đối xứng với A qua có tọa độ là
.
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng ![]() . Khoảng cách giữa AB và trục của hình trụ bằng:
. Khoảng cách giữa AB và trục của hình trụ bằng:
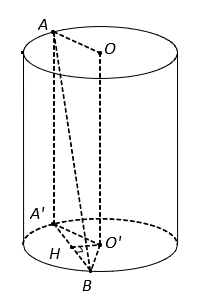
Từ hình vẽ kết hợp với giả thiết, ta có .
Gọi AA’ là đường sinh của hình trụ thì và
.
Vì nên
Gọi H là trung điểm A’B, suy ra
nên .
Tam giác ABA’ vuông tại A’ nên
Suy ra tam giác A’BO đều có cạnh bằng R nên
Gọi F(x) là một nguyên hàm của hàm số ![]() thỏa mãn
thỏa mãn ![]() . Tính
. Tính ![]() .
.
Cho các hàm số ![]() và
và ![]() liên tục trên
liên tục trên ![]() thỏa mãn
thỏa mãn ![]() với
với ![]() . Tính
. Tính ![]() , biết rằng
, biết rằng ![]() ?
?
Ta có: .
Cho hình vẽ:

Diện tích hình phẳng (phần gạch chéo) giới hạn bởi đồ thị 3 hàm số ![]() như hình bên, bằng kết quả nào sau đây?
như hình bên, bằng kết quả nào sau đây?
Diện tích miền tích phân được chia thành hai phần. Phần 1 với x nằm trong khoảng a đến b và phần 2 với x nằm trong khoảng b đến c:
.
Họ nguyên hàm của hàm số ![]() là:
là:
Ta có:
Khi đó:
Tìm nguyên hàm ![]() của hàm số
của hàm số ![]() , biết rằng
, biết rằng ![]() ?
?
Ta có:
Vậy .
Trong không gian ![]() , cho bốn điểm
, cho bốn điểm ![]() . Hai điểm
. Hai điểm ![]() lần lượt nằm trên đoạn BC và BD sao cho
lần lượt nằm trên đoạn BC và BD sao cho ![]() và
và ![]() . Phương trình mặt phẳng
. Phương trình mặt phẳng ![]() có dạng
có dạng ![]() . Tính
. Tính ![]() ?
?
Trong không gian , cho bốn điểm
. Hai điểm
lần lượt nằm trên đoạn BC và BD sao cho
và
. Phương trình mặt phẳng
có dạng
. Tính
?
Cho hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() và
và ![]() là một nguyên hàm của
là một nguyên hàm của ![]() . Biết rằng
. Biết rằng ![]() . Xác định tích phân
. Xác định tích phân ![]() ?
?
Ta có: .
Tìm họ các nguyên hàm của hàm số ![]() ?
?
Ta có:
Trong không gian ![]() , cho hai vecto
, cho hai vecto ![]() ,
, ![]() cùng có độ dài bằng
cùng có độ dài bằng ![]() . Biết rằng góc giữa hai vecto đó bằng
. Biết rằng góc giữa hai vecto đó bằng ![]() , giá trị của biểu thức
, giá trị của biểu thức ![]() là
là
Ta có:
Do đó:
.
