Cho hình trụ có bán kính đáy bằng R và chiều cao bằng ![]() . Mặt phẳng
. Mặt phẳng ![]() song song với trục của hình trụ và cách trục một khoảng bằng
song song với trục của hình trụ và cách trục một khoảng bằng ![]() . Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng ![]() là:
là:
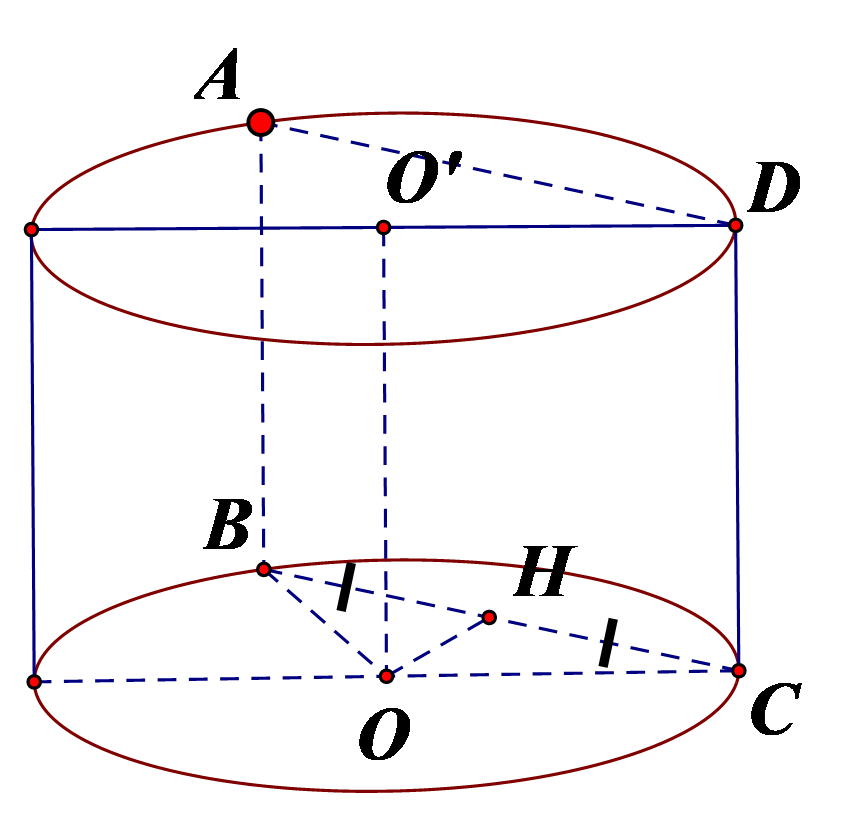
Giả sử thiết diện là hình chữ nhật ABCD như hình vẽ.
Gọi H là trung điểm BC suy ra suy ra
Khi đó
Suy ra .