Tính diện tích hình phẳng giới hạn bởi hai đồ thị ![]() và
và ![]() ?
?
Phương trình hoành độ giao điểm
Diện tích hình giới hạn là
Tính diện tích hình phẳng giới hạn bởi hai đồ thị ![]() và
và ![]() ?
?
Phương trình hoành độ giao điểm
Diện tích hình giới hạn là
Một chiếc máy bay đang bay từ điểm ![]() đến điểm
đến điểm ![]() . Giả sử với đơn vị km, điểm
. Giả sử với đơn vị km, điểm![]() có tọa độ
có tọa độ ![]() và điểm
và điểm ![]() có tọa độ
có tọa độ ![]() . Máy bay được trạm không lưu thông báo có một cơn bão với tâm bão ở vị trí
. Máy bay được trạm không lưu thông báo có một cơn bão với tâm bão ở vị trí ![]() với tọa độ
với tọa độ ![]() , máy bay được an toàn khi cách tâm bão tối thiểu là
, máy bay được an toàn khi cách tâm bão tối thiểu là ![]() . Tính gọi
. Tính gọi ![]() là điểm trên đường bay (giữa
là điểm trên đường bay (giữa ![]() và
và ![]() ) mà máy bay cần chuyển hướng để tránh cơn bão. Tính độ dài quãng đường
) mà máy bay cần chuyển hướng để tránh cơn bão. Tính độ dài quãng đường ![]() (kết quả lấy phần nguyên).
(kết quả lấy phần nguyên).
Đáp án: 173,21 km
Một chiếc máy bay đang bay từ điểm đến điểm
. Giả sử với đơn vị km, điểm
có tọa độ
và điểm
có tọa độ
. Máy bay được trạm không lưu thông báo có một cơn bão với tâm bão ở vị trí
với tọa độ
, máy bay được an toàn khi cách tâm bão tối thiểu là
. Tính gọi
là điểm trên đường bay (giữa
và
) mà máy bay cần chuyển hướng để tránh cơn bão. Tính độ dài quãng đường
(kết quả lấy phần nguyên).
Đáp án: 173,21 km
Hình vẽ minh họa
Giả sử
Vì là điểm trên đường bay (giữa
và
). Khi đó ta có ba điểm
thẳng hàng.
Ta lại có là điểm mà máy bay cần chuyển hướng để tránh cơn bão.
Khi đó
Ta có hệ phương trình:
Giải (*) ta có
Vì là điểm gần
hơn do đó chọn
hay
Vậy độ dài quãng đường:
Giả sử hàm số f(x) luôn xác định. Tìm họ nguyên hàm của hàm số ![]()
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng ![]() . Khoảng cách giữa AB và trục của hình trụ bằng:
. Khoảng cách giữa AB và trục của hình trụ bằng:
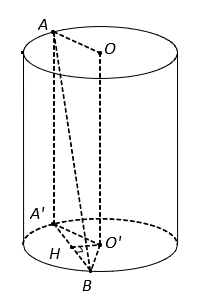
Từ hình vẽ kết hợp với giả thiết, ta có .
Gọi AA’ là đường sinh của hình trụ thì và
.
Vì nên
Gọi H là trung điểm A’B, suy ra
nên .
Tam giác ABA’ vuông tại A’ nên
Suy ra tam giác A’BO đều có cạnh bằng R nên
Một ô tô đang chạy đều với vận tốc ![]() thì người lái xe đạp phanh. Từ thời điểm ô tô chuyển động chậm dần đều với vận tốc
thì người lái xe đạp phanh. Từ thời điểm ô tô chuyển động chậm dần đều với vận tốc ![]() . Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 56m. Tính giá trị của
. Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 56m. Tính giá trị của ![]() ?
?
Khi dừng hẳn
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là:
Cho ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() thỏa mãn
thỏa mãn ![]() . Tìm
. Tìm ![]() ?
?
Ta có:
Lại có
Vậy .
Cho tứ diện ![]() , có
, có ![]() đôi một vuông góc,
đôi một vuông góc, ![]() là điểm thuộc miền trong của tam giác
là điểm thuộc miền trong của tam giác ![]() . Gọi khoảng cách từ
. Gọi khoảng cách từ ![]() đến các mặt phẳng
đến các mặt phẳng ![]() lần lượt là
lần lượt là ![]() . Tính độ dài đoạn
. Tính độ dài đoạn ![]() sao cho tứ diện
sao cho tứ diện ![]() có thể tích nhỏ nhất.
có thể tích nhỏ nhất.
Xét hệ trục tọa độ Oxyz sao cho A thuộc tia Ox; B thuộc tia Oy và C thuộc tia Oz.
Ta có
Ta có:
Đẳng thức xảy ra khi chỉ khi
Tích phân  có giá trị là:
có giá trị là:
Ta có:
Đặt
Đổi cận
Tìm họ nguyên hàm của hàm số ![]()
Cho hàm số y = f(x) liên tục, f(x) nhận giá trị dương trên ![]() và thỏa mãn f(1) = 1,
và thỏa mãn f(1) = 1, ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Ta có: và
=>
=>
Mà f(1) = 1 => và
Một khối cầu có bán kính ![]() , người ta cắt bỏ
, người ta cắt bỏ ![]() phần bằng
phần bằng ![]() mặt phẳng song song và vuông góc với bán kính, hai mặt phẳng đó đều cách tâm của khối cầu
mặt phẳng song song và vuông góc với bán kính, hai mặt phẳng đó đều cách tâm của khối cầu ![]() để làm một chiếc lu đựng nước. Tính thể tích nước mà chiếc lu chứa được (coi độ dày của bề mặt không đáng kể).
để làm một chiếc lu đựng nước. Tính thể tích nước mà chiếc lu chứa được (coi độ dày của bề mặt không đáng kể).
Hình vẽ minh họa
Đặt trục tọa độ như hình vẽ. Thể tích cái được tính bằng cách cho đường tròn có phương trình quay quanh trục Ox.
Thể tích cái lu bằng;
Trong không gian với hệ trục tọa độ ![]() , cho hình bình hành
, cho hình bình hành ![]() . Biết
. Biết ![]() và
và ![]() . Diện tích hình bình hành
. Diện tích hình bình hành ![]() là:
là:
Ta có:
Suy ra diện tích ABCD là:
Cho hàm số ![]() có một nguyên hàm là
có một nguyên hàm là ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() liên túc trên
liên túc trên ![]() . Giá trị biểu thức
. Giá trị biểu thức ![]() bằng:
bằng:
Ta có:
Vì hàm số liên tục trên
nên liên tục tại
tức là
Do đó
Trong không gian hệ trục tọa độ ![]() , cho ba điểm
, cho ba điểm ![]() . Tìm điểm
. Tìm điểm ![]() sao cho
sao cho ![]() đạt giá trị nhỏ nhất?
đạt giá trị nhỏ nhất?
Vì suy ra
. Ta có:
Theo bài ra:
Vậy nhỏ nhất bằng
khi
. Hay
Tích tất cả giá trị của ![]() để góc tạo bởi đường thẳng
để góc tạo bởi đường thẳng ![]() và đường thẳng
và đường thẳng ![]() bằng
bằng ![]() là:
là:
Đáp án: -4||- 4
Tích tất cả giá trị của để góc tạo bởi đường thẳng
và đường thẳng
bằng
là:
Đáp án: -4||- 4
Gọi là góc giữa hai đường thẳng đã cho.
Đường thẳng có vectơ chỉ phương là
.
Đường thẳng có vectơ chỉ phương là
.
Ta có:
Vậy tích tất cả các giá trị của tham số a bằng -4.
Tìm nguyên hàm của hàm số ![]() ?
?
Ta có:
Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng ![]() . Diện tích toàn phần của hình nón là:
. Diện tích toàn phần của hình nón là:
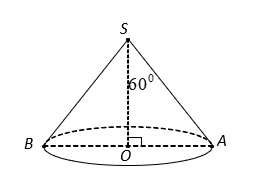
Gọi S là đỉnh, O là tâm của đáy, thiết diện qua trục là SAB.
Theo giả thiết, ta có và
.
Trong tam giác SAO vuông tại O, ta có
Vậy diện tích toàn phần:
(đvdt).
Cho hai điểm ![]() và mặt phẳng
và mặt phẳng ![]() Mặt phẳng
Mặt phẳng ![]() chứa hai điểm A,B và vuông góc với mặt phẳng
chứa hai điểm A,B và vuông góc với mặt phẳng ![]() có phương trình:
có phương trình:
Theo đề bài, ta có: ;
Suy ra ;
có vectơ pháp tuyến
Ta có cùng phương với vectơ
Chọn làm 1 vectơ pháp tuyến cho mặt phẳng
.
Phương trình mặt phẳng có dạng:
Mặt phẳng :
Cho hàm số ![]() xác định trên
xác định trên ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Hệ số góc của phương trình tiếp tuyến của đồ thị hàm số
. Hệ số góc của phương trình tiếp tuyến của đồ thị hàm số ![]() tại giao điểm với trục hoành là:
tại giao điểm với trục hoành là:
Ta có:
Lấy nguyên hàm hai vế ta được:
Lại có
Từ đó suy ra
Xét phương trình hoành độ giao điểm
Ta có:
Vậy hệ số góc phương trình tiếp tuyến cần tìm là 1.
Cho hàm số ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Ta có:
.
Theo bài ra ta có:
Vậy .
Trong không gian ![]() , phương trình nào sau đây là phương trình của mặt phẳng?
, phương trình nào sau đây là phương trình của mặt phẳng?
Phương trình tổng quát của mặt phẳng là: .
Giả sử ![]() là các hàm số bất kì liên tục trên
là các hàm số bất kì liên tục trên ![]() và
và ![]() là các số thực. Mệnh đề nào sau đây sai?
là các số thực. Mệnh đề nào sau đây sai?
Theo tính chất tích phân ta có:
Vậy mệnh đề sai:
Trong không gian với hệ trục tọa độ ![]() , cho ba điểm
, cho ba điểm ![]() . Điểm
. Điểm ![]() là đỉnh thứ tư của hình bình hành
là đỉnh thứ tư của hình bình hành ![]() . Khi đó giá trị biểu thức
. Khi đó giá trị biểu thức ![]() có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
Gọi tọa độ điểm
Ta có:
Ta có: là hình bình hành
suy ra điểm
Khi đó .
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số ![]() quanh trục
quanh trục ![]() bằng
bằng
Ta có:
Dòng diện xoay chiều hình sin chạy qua mạch điện dao động ![]() lí tưởng có phương trình
lí tưởng có phương trình ![]() . Ngoài ra
. Ngoài ra ![]() với
với ![]() là điện tích tức thời trong tụ. Tính từ lúc
là điện tích tức thời trong tụ. Tính từ lúc ![]() , điện lượng chạy qua tiết diện thẳng của dây dẫn của mạch trong thời gian
, điện lượng chạy qua tiết diện thẳng của dây dẫn của mạch trong thời gian ![]() là
là
Điện lượng cần tìm là:
Cho hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() . Gọi
. Gọi ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() . Thể tích khối tròn xoay tạo thành khi quay
. Thể tích khối tròn xoay tạo thành khi quay ![]() quanh trục hoành được tính theo công thức:
quanh trục hoành được tính theo công thức:
Thể tích của khối tròn xoay cần tính là:
Trong không gian hệ trục tọa độ ![]() , điểm nào dưới đây thuộc trục
, điểm nào dưới đây thuộc trục ![]() ?
?
Điểm . Suy ra trong bốn điểm đã cho điểm
.
Trong không gian Oxyz, mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và vuông góc với trục Ox có phương trình là:
và vuông góc với trục Ox có phương trình là:
Ta có: .
Phương trình mặt phẳng đi qua và vuông góc với trục Ox có phương trình là:
Trong không gian ![]() , phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm
, phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm ![]() và song song với mặt phẳng
và song song với mặt phẳng ![]() ?
?
Mặt phẳng có phương trình là
nên có một vectơ pháp tuyến là
.
Phương trình của mặt phẳng cần tìm có dạng
.
Tìm nguyên hàm của hàm số ![]() ??
??
Đặt
Hình nón có đường sinh ![]() và hợp với đáy góc
và hợp với đáy góc ![]() . Diện tích toàn phần của hình nón bằng:
. Diện tích toàn phần của hình nón bằng:
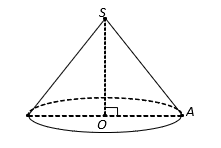
Theo giả thiết, ta có
và
.
Suy ra:
.
Vậy diện tích toàn phần của hình nón bằng: (đvdt).
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:
Gọi bán kính đáy là R.
Hình trụ có chu vi đáy bằng 2a nên ta có .
Suy ra hình trụ này có đường cao .
Vậy thể tích khối trụ (đvtt).
Tìm nguyên hàm của hàm số ![]() là
là
Ta có:
Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu giá của ba vectơ cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.
Diện tích hình phẳng giới hạn bởi các đường ![]() , trục hoành,
, trục hoành, ![]() và
và ![]() bằng
bằng
Diện tích hình giới hạn là
Công thức diện tích hình phẳng giới hạn bởi đồ thị hàm số ![]() ,
, ![]() liên tục trên đoạn
liên tục trên đoạn ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]()
![]() là
là
Diện tích hình phẳng giới hạn bởi đồ thị hàm số ,
liên tục trên đoạn
và hai đường thẳng
,
là
.
Cho hình trụ có bán kính đáy bằng R và chiều cao bằng ![]() . Mặt phẳng
. Mặt phẳng ![]() song song với trục của hình trụ và cách trục một khoảng bằng
song song với trục của hình trụ và cách trục một khoảng bằng ![]() . Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng ![]() là:
là:
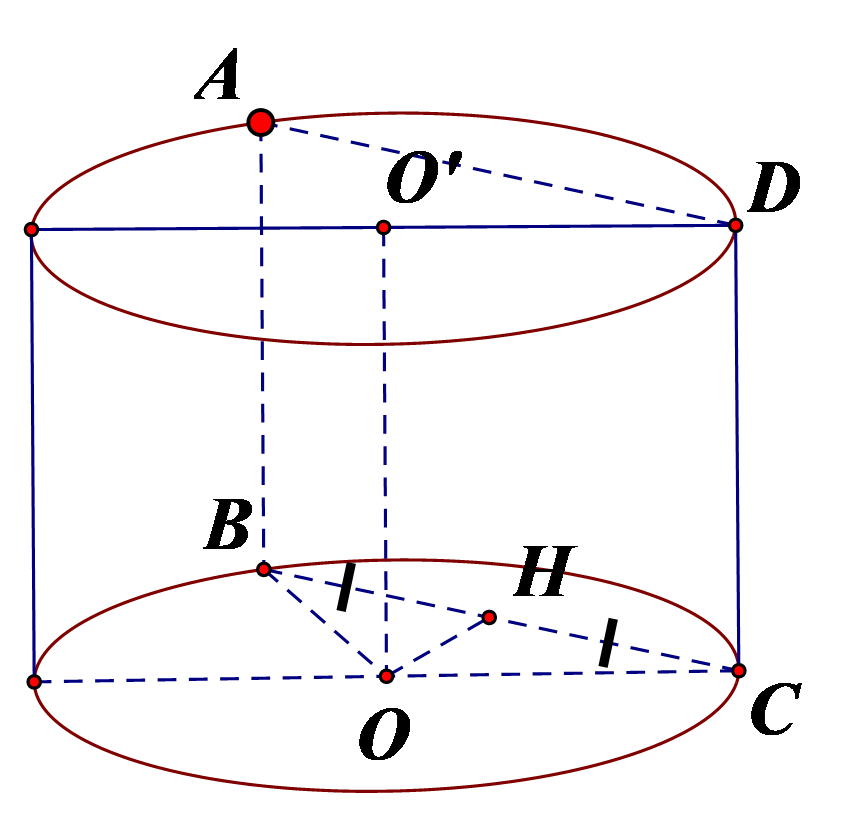
Giả sử thiết diện là hình chữ nhật ABCD như hình vẽ.
Gọi H là trung điểm BC suy ra suy ra
Khi đó
Suy ra .
Cho hàm số ![]() . Tính
. Tính ![]()
Ta có:
.
Cho ![]() . Với
. Với ![]() , khẳng định nào sau đây đúng?
, khẳng định nào sau đây đúng?
Xét , đặt t = ax + b
=>
=>
Trong không gian với hệ tọa độ ![]() , cho các điểm
, cho các điểm ![]() . Phương trình mặt phẳng
. Phương trình mặt phẳng ![]() nào dưới đây đi qua
nào dưới đây đi qua ![]() , gốc tọa độ
, gốc tọa độ ![]() và cách đều hai điểm
và cách đều hai điểm ![]() và
và ![]() ?
?
Vì đi qua O nên phương trình mặt phẳng
có dạng
.
Vì A ∈ (P) và B, C cách đều (P) nên
Chọn a = −6, ta có b = 3, suy ra c = ±4.
Vậy có hai mặt phẳng thỏa mãn là hoặc
.
