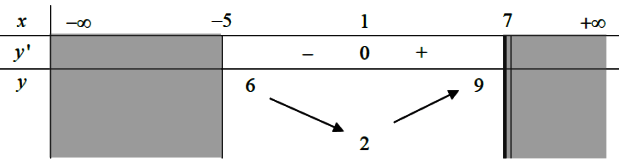Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo Đề 5

Mô tả thêm: Đề thi giữa HK1 Toán 12 được biên soạn bám sát chương trình sách chân trời sáng tạo giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức

Thời gian làm: 90 phút
Số câu hỏi: 22 câu
Số điểm tối đa: 22 điểm
Tài khoản: Đăng nhập

Mua gói để Làm bài

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Câu 1: Nhận biết
Cho hàm số $y = f(x)$ xác định và liên tục trên khoảng $( - \infty; + \infty)$ , có bảng biến thiên như hình sau:

Mệnh đề nào sau đây đúng?
- A.
  Hàm số nghịch biến trên khoảng $( - \infty;1)$ .
- B.
  Hàm số đồng biến trên khoảng $( - 1; + \infty)$ .
- C.
  Hàm số nghịch biến trên khoảng $(1; + \infty)$ .
- D.
  Hàm số đồng biến trên khoảng $( - \infty; - 2)$ .
Dựa vào bảng biến thiên ta thấy:

Hàm số nghịch biến trên khoảng $( - 1;1)$

Hàm số đồng biến trên khoảng $( - \infty; - 1) \cup (1; + \infty)$

Vậy đáp án cần tìm là: “Hàm số đồng biến trên khoảng $( - \infty; - 2)$ ”.
Câu 2: Nhận biết
Cho hình vẽ là đồ thị hàm số $y = f'(x)$ . Hỏi hàm số $y = f(x)$ đồng biến trên khoảng nào dưới đây?
- A.
  $(2; + \infty)$
- B.
  $(0;1)$ và $(1; + \infty)$
- C.
  $(0;1)$
- D.
  $(1;2)$
Từ đồ thị $y = f'(x)$ ta có bảng xét dấu $y = f'(x)$ như sau:
Vậy hàm số đồng biến trên khoảng $(0;1)$
Câu 3: Thông hiểu
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y = x^{3} - 3mx^{2} + 3\left( m^{2} - 2 ight)x$ đồng biến trên khoảng $(12; + \infty)$ ?
- A.
  $11$
- B.
  $10$
- C.
  $13$
- D.
  $0$
Ta có: $y' = 3x^{2} - 6mx + 3\left( m^{2} - 2 ight)$

Hàm số $y = x^{3} - 3mx^{2} + 3\left( m^{2} - 2 ight)x$ đồng biến trên khoảng $(12; + \infty)$

$\Leftrightarrow y' \geq 0 \Leftrightarrow 3x^{2} - 6mx + 3\left( m^{2} - 2 ight) \geq 0$

$\Leftrightarrow x^{2} - 2mx + m^{2} - 2 \geq 0$

$\Leftrightarrow (x - m)^{2} \geq 2 \Leftrightarrow \left\lbrack \begin{matrix} x - m \geq \sqrt{2} \\ x - m \leq - \sqrt{2} \\ \end{matrix} ight.$

$\Leftrightarrow \left\lbrack \begin{matrix} x \geq m + \sqrt{2} \\ x \leq m - \sqrt{2} \\ \end{matrix} ight.$

Theo yêu cầu bài toán ta có: $\sqrt{2} + m \leq 12 \Leftrightarrow m \leq 12 - \sqrt{2}$

Mà $m\mathbb{\in Z \Rightarrow}m \in \left\{ 1;2;3;...;9;10 ight\}$

Suy ra có tất cả 10 giá trị nguyên của tham số m thỏa mãn yêu cầu đề bài.
Câu 4: Nhận biết
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Kết luận nào sau đây đúng?
- A.
  Hàm số có hai điểm cực đại.
- B.
  Hàm số có bốn điểm cực trị.
- C.
  Hàm số có hai điểm cực trị.
- D.
  Hàm số có hai điểm cực tiểu.
Dựa vào bảng xét dấu đạo hàm ta thấy: hàm số đạt cực trị tại $x = 1;x = 3;x = 4$ .

Tại $x = 1;x = 4$ ta thấy $f'(x)$ đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại $x = 1;x = 4$ .

Tại $x = 3$ ta thấy $f'(x)$ đổi dấu từ dương sang âm nên hàm số đạt cực đại tại $x = 3$ .
Câu 5: Nhận biết
Cho hàm số $f(x) = x^{3} - 3x$ . Tìm giá trị nhỏ nhất của hàm số đã cho trên đoạn $\lbrack - 2;1brack$ ?
- A.
  $2$
- B.
  $- 2$
- C.
  $3$
- D.
  $- 3$
Xét hàm số $f(x) = x^{3} - 3x$ xác định trên tập số thực có:

$f'(x) = 3x^{2} - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 1 \\ \end{matrix} ight.$

$\Rightarrow \left\{ \begin{matrix} f( - 2) = - 2 \\ f(1) = - 2 \\ f( - 1) = 2 \\ \end{matrix} ight.\ \Rightarrow \min_{\lbrack - 2;1brack}f(x) = - 2$

Vậy giá trị nhỏ nhất của hàm số là -2 khi x = 1 hoặc x = -2.
Câu 6: Nhận biết
Cho hàm số y = f(x) và có bảng biến thiên trên [-5; 7) như sau:
Mệnh đề nào sau đây đúng?
- A. $\mathop {\min }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 2$ và hàm số không đạt giá trị lớn nhất trên [-5; 7)
- B. $\mathop {\max }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 6$ và $\mathop {\min }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 2$
- C. $\mathop {\max }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 9$ và $\mathop {\min }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 2$
- D. $\mathop {\max }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 9$ và $\mathop {\min }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 6$
Dựa vào bảng biến thiên dễ dàng ta thấy $\mathop {\min }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 2$
$\mathop {\max }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 6$ là sai vì f(x) sẽ nhận các giá trị 7; 8 lớn hơn 6 khi x tiến tới 7
$\mathop {\max }\limits_{\left[ { - 5;7} ight)} f\left( x ight) = 9$ là sai vì f(x) không bằng 9 mà chỉ tiến đến 9 khi x dần đến 7 (x khác 7)
Vậy chọn đáp án A.
Câu 7: Nhận biết
Tâm đối xứng của đồ thị hàm số $y = \frac{3x - 1}{x + 2}$ là điểm nào sau đây?
- A.
  $( - 2;3)$
- B.
  $(3; - 2)$
- C.
  $(2; - 1)$
- D.
  $( - 1;2)$
Đồ thị hàm số $y = \frac{3x - 1}{x + 2}$ có tiệm cận đứng $x = - 2$ , tiệm cận ngang $y = 3$

Suy ra tâm đối xứng là $( - 2;3)$ .
Câu 8: Thông hiểu
Xác định số đường tiệm cận của đồ thị hàm số $y = \frac{\sqrt{x^{2} + 1}}{x + 1}$ ?
- A.
  $2$
- B.
  $3$
- C.
  $1$
- D.
  $0$
Tập xác định $D\mathbb{= R}\backslash\left\{ - 1 ight\}$

Vì $\lim_{x ightarrow - 1^{+}}f(x) = + \infty$ nên đồ thị hàm số nhận đường thẳng $x = - 1$ làm đường tiệm cận đứng.

Vì $\lim_{x ightarrow - \infty}f(x) =\lim_{x ightarrow - \infty}\dfrac{\sqrt{x^{2} + 1}}{x + 1} = \lim_{xightarrow - \infty}\dfrac{- \sqrt{1 + \dfrac{1}{x^{2}}}}{1 +\dfrac{1}{x}} = - 1$ nên đồ thị hàm số nhận đường thẳng $y = - 1$ làm đường tiệm cận ngang.

Vì $\lim_{x ightarrow + \infty}f(x) =\lim_{x ightarrow + \infty}\dfrac{\sqrt{x^{2} + 1}}{x + 1} = \lim_{xightarrow + \infty}\dfrac{\sqrt{1 + \dfrac{1}{x^{2}}}}{1 + \dfrac{1}{x}}= 1$ nên đồ thị hàm số nhận đường thẳng $y = 1$ làm đường tiệm cận ngang.

vậy đồ thị hàm số có tổng số đường tiệm cận bằng 3.
Câu 9: Nhận biết
Số giao điểm của hai đồ thị hàm số $y = f(x)$ và $y = g(x)$ bằng số nghiệm phân biệt của phương trình nào sau đây?
- A.
  $\frac{f(x)}{g(x)} = 0$
- B.
  $f(x) + g(x) = 0$
- C.
  $f(x) - g(x) = 0$
- D.
  $f(x)g(x) = 0$
Hoành độ giao điểm là nghiệm của phương trình $f(x) = g(x)$ hay $f(x) - g(x) = 0$ .
Câu 10: Thông hiểu
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

Tổng các giá trị nguyên của tham số $m$ để đường thẳng $y = m$ cắt đồ thị hàm số tại ba điểm phân biệt bằng bao nhiêu?
- A.
  $0$
- B.
  $- 3$
- C.
  $- 5$
- D.
  $- 1$
Hình vẽ minh họa

Đường thẳng $y = m$ cắt đồ thị hàm số tại ba điểm phân biệt $\Leftrightarrow - 4 < m < 2$

Mà $m\mathbb{\in Z \Rightarrow}m \in \left\{ - 3; - 2; - 1;0;1 ight\}$

Vậy tổng tất cả các giá trị nguyên của tham số m thỏa mãn yêu cầu bằng -5.
Câu 11: Nhận biết
Cho hai điểm phân biệt $A;B$ và một điểm $O$ bất kì. Hãy xét xem mệnh đề nào sau đây là đúng?
- A.
  Điểm $M$ thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow{OM} = \overrightarrow{OB} = k.\overrightarrow{BA}$ .
- B.
  Điểm $M$ thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow{OM} = k.\left( \overrightarrow{OB} - \overrightarrow{OA} ight)$ .
- C.
  Điểm $M$ thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow{OM} = k\overrightarrow{OA} + (1 - k).\overrightarrow{OB}$ .
- D.
  Điểm $M$ thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow{OM} = \overrightarrow{OA} + \overrightarrow{OB}$ .
Mệnh đề đúng: “Điểm $M$ thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow{OM} = k\overrightarrow{OA} + (1 - k).\overrightarrow{OB}$ ”.
Câu 12: Nhận biết
Điều kiện cần và đủ để ba vectơ $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ không đồng phẳng là:
- A.
  Giá của chúng không cùng thuộc một mặt phẳng.
- B.
  Giá của chúng cùng thuộc một mặt phẳng.
- C.
  Giá của chúng không cùng song song với một mặt phẳng.
- D.
  Giá của chúng cùng song song với một mặt phẳng.
Ba vectơ $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ đồng phẳng khi và chỉ khi giá của chúng cùng song song với một mặt phẳng.
Câu 13: Nhận biết

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\left\{ \pm 2 ight\}$ và có bảng biến thiên như sau:

Xét tính đúng sai của các khẳng định sau.

a) Hàm số không có điểm cực trị. Đúng||Sai

b) $\lim_{x ightarrow ( - 2)^{-}}f(x) = + \infty$ . Sai||Đúng

c) Đồ thị hàm số có đúng 1 tiệm cận ngang. Đúng||Sai

d) Đồ thị hàm số có đúng 1 tiệm cận đứng. Sai||Đúng

Đáp án là:

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\left\{ \pm 2 ight\}$ và có bảng biến thiên như sau:

Xét tính đúng sai của các khẳng định sau.

a) Hàm số không có điểm cực trị. Đúng||Sai

b) $\lim_{x ightarrow ( - 2)^{-}}f(x) = + \infty$ . Sai||Đúng

c) Đồ thị hàm số có đúng 1 tiệm cận ngang. Đúng||Sai

d) Đồ thị hàm số có đúng 1 tiệm cận đứng. Sai||Đúng

Dựa vào bảng biến thiên ta thấy

a) Hàm số không có điểm cực trị.

b) lim $\lim_{x ightarrow ( - 2)^{-}}f(x) = - 10$ .

c) $\lim_{x ightarrow \pm \infty}f(x) = 0$ . Suy ra đồ thị có đúng 1 đường tiệm cận ngang là $y = 0$ .

d) $\lim_{x ightarrow ( - 2)^{+}}f(x) = + \infty$ và $\lim_{x ightarrow 2^{+}}f(x) = + \infty$ nên đồ thị hàm số có đúng 2 đường tiệm cận đứng $x = \pm 2$ .
Câu 14: Thông hiểu

Cho hàm số $y = f(x) = x^{2} - 4\ln(1 -x)$ . Xét tính đúng sai của các khẳng định sau:

a) Tập xác định của hàm số là $D = (1; + \infty)$ . Sai||Đúng

b) Đạo hàm của hàm số là $y' = \frac{- 2x^{2} + 2x + 4}{1 - x}$ . Đúng||Sai

c) Giá trị lớn nhất của hàm số trên $\lbrack - 2;0brack$ là 2. Sai||Đúng

d) Giá trị nhỏ nhất của hàm số trên $\lbrack - 2;0brack$ là $1 - 4\ln2$ . Đúng||Sai

Đáp án là:

Cho hàm số $y = f(x) = x^{2} - 4\ln(1 -x)$ . Xét tính đúng sai của các khẳng định sau:

a) Tập xác định của hàm số là $D = (1; + \infty)$ . Sai||Đúng

b) Đạo hàm của hàm số là $y' = \frac{- 2x^{2} + 2x + 4}{1 - x}$ . Đúng||Sai

c) Giá trị lớn nhất của hàm số trên $\lbrack - 2;0brack$ là 2. Sai||Đúng

d) Giá trị nhỏ nhất của hàm số trên $\lbrack - 2;0brack$ là $1 - 4\ln2$ . Đúng||Sai

Tập xác định của hàm số là $D = (1; + \infty)$ .

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

Ta có: $y' = 2x + \frac{4}{1 - x} = \frac{- 2x^{2} + 2x + 4}{1 - x}$

Khi đó $y' = 0 \Leftrightarrow \frac{- 2x^{2} + 2x + 4}{1 - x} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1(TM) \\ x = 2(L) \\ \end{matrix} ight.$

Ta có: $\left\{ \begin{matrix}f( - 2) = 4 - 4\ln3 \\f( - 1) = 1 - 4\ln2 \\f(0) = 0 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}M = 0 \\m = 1 - 4\ln2 \\\end{matrix} ight.$
Câu 15: Thông hiểu

Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích $1800m^{3}$ và chiều sâu $2m$ (như hình vẽ).

Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

Xét tính đúng sai của các khẳng định sau:

a) Thể tích bể chứa được tính theo công thức $V = 2x^{2}y$ . Sai|| Đúng

b) Mối liên hệ giữa x và y là $y = \frac{900}{x}$ . Đúng||Sai

c) Tổng diện tích mặt bên của bể tính theo x, y là $S = 4(x + y)$ . Đúng||Sai

d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là $40m$ . Sai|| Đúng

Đáp án là:

Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích $1800m^{3}$ và chiều sâu $2m$ (như hình vẽ).

Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

Xét tính đúng sai của các khẳng định sau:

a) Thể tích bể chứa được tính theo công thức $V = 2x^{2}y$ . Sai|| Đúng

b) Mối liên hệ giữa x và y là $y = \frac{900}{x}$ . Đúng||Sai

c) Tổng diện tích mặt bên của bể tính theo x, y là $S = 4(x + y)$ . Đúng||Sai

d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là $40m$ . Sai|| Đúng

a) Thể tích của bể là $V = B.h = xy.\ h$ .

b) Với $V = xy.h \Rightarrow 1800 = xy.2 \Rightarrow xy = \frac{1800}{2} = 900$ .

c) Tổng diện tích mặt bên gồm 4 hình chữ nhật (trước, sau, trái, phải) là:

$\ S = 2x + 2x + 2y + 2y = 4x + 4y = 4(x + y)$

d) Tổng diện tích của bể là: $4x + 4y + xy = 4x + 4.\frac{900}{x} + 900$

Vì chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể nên chi phí cần có là $4x + 4.\frac{900}{x} + 2.900$

Đặt $f(x) = 4x + 4.\frac{900}{x} + 1800$ ta có: $f'(x) = 4 - \frac{3600}{x^{2}} \Rightarrow f'(x) = 0 \Leftrightarrow x = 30$ ta có bảng biến thiên như sau:

Với $x = 30m;y = 30 m$ và thì chi phí xây dựng bể là thấp nhất.
Câu 16: Thông hiểu

Cho tứ diện $ABCD$ . Gọi $M, N$ theo thứ tự là trung điểm $AB$ và $CD$ . Khẳng định nào sau đây đúng?

Xác định tính đúng sai của các khẳng định sau:

a) $\overrightarrow{MC} + \overrightarrow{MD} + \overrightarrow{NA} + \overrightarrow{NB} = 4\overrightarrow{MN}$ Sai||Đúng

b) $\overrightarrow{AC} + \overrightarrow{BD} = 2\overrightarrow{MN}$ Đúng||Sai

c) $\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{MN}$ Sai||Đúng

d) $\overrightarrow{AC} + \overrightarrow{AD} = 2\overrightarrow{AN}$ Đúng||Sai

Đáp án là:

Cho tứ diện $ABCD$ . Gọi $M, N$ theo thứ tự là trung điểm $AB$ và $CD$ . Khẳng định nào sau đây đúng?

Xác định tính đúng sai của các khẳng định sau:

a) $\overrightarrow{MC} + \overrightarrow{MD} + \overrightarrow{NA} + \overrightarrow{NB} = 4\overrightarrow{MN}$ Sai||Đúng

b) $\overrightarrow{AC} + \overrightarrow{BD} = 2\overrightarrow{MN}$ Đúng||Sai

c) $\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{MN}$ Sai||Đúng

d) $\overrightarrow{AC} + \overrightarrow{AD} = 2\overrightarrow{AN}$ Đúng||Sai

a) Vì $M, N$ là trung điểm của $AB$ và $CD$ nên $\overrightarrow{MC} + \overrightarrow{MD} = 2\overrightarrow{MN}$ và $\overrightarrow{NA} + \overrightarrow{NB} = 2\overrightarrow{NM}$

Nên $\overrightarrow{MC} + \overrightarrow{MD} + \overrightarrow{NA} + \overrightarrow{NB} = \overrightarrow{0}$ .

b) Ta có:

$\overrightarrow{AC} + \overrightarrow{BD} = \overrightarrow{AM} + \overrightarrow{MC} + \overrightarrow{BM} + \overrightarrow{MD}$

$= \left( \overrightarrow{AM} + \overrightarrow{BM} ight) + \left( \overrightarrow{MC} + \overrightarrow{MD} ight)$

$= \overrightarrow{0} + 2\overrightarrow{MN} = 2\overrightarrow{MN}$

c) Ta có:

$\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AC} + \overrightarrow{CD} + \overrightarrow{BD} + \overrightarrow{DC}$

$= \left( \overrightarrow{AC} + \overrightarrow{BD} ight) + \left( \overrightarrow{CD} + \overrightarrow{DC} ight) = \overrightarrow{AC} + \overrightarrow{BD} = 2\overrightarrow{MN}$

d) Do N là trung điểm của CD nên $\overrightarrow{AC} + \overrightarrow{AD} = 2\overrightarrow{AN}$
Câu 17: Thông hiểu

Xác định số giá trị nguyên của tham số $m$ để hàm số $y = \frac{mx - 2}{- 2x +m}$ nghịch biến trên khoảng $\left(\frac{1}{2}; + \infty ight)$ ?
Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Xác định số giá trị nguyên của tham số $m$ để hàm số $y = \frac{mx - 2}{- 2x +m}$ nghịch biến trên khoảng $\left(\frac{1}{2}; + \infty ight)$ ?
Chỗ nhập nội dung câu trả lời tự luận
Câu 18: Thông hiểu

Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật $s(t) = t^{3} - 4t^{2} + 12(m)$ , trong đó $t(s)$ là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi $t$ bằng bao nhiêu?

Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật $s(t) = t^{3} - 4t^{2} + 12(m)$ , trong đó $t(s)$ là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi $t$ bằng bao nhiêu?

Chỗ nhập nội dung câu trả lời tự luận
Câu 19: Vận dụng

Cho hàm số $y = \frac{x + 1}{\sqrt{ax^{2}+ 1}}$ có đồ thị $(C)$ . Tìm giá trị $a$ để đồ thị hàm số có đường tiệm cận và đường tiệm cận đó cách đường tiếp tuyến của $(C)$ một khoảng bằng $\sqrt{2} - 1$ ?
Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Cho hàm số $y = \frac{x + 1}{\sqrt{ax^{2}+ 1}}$ có đồ thị $(C)$ . Tìm giá trị $a$ để đồ thị hàm số có đường tiệm cận và đường tiệm cận đó cách đường tiếp tuyến của $(C)$ một khoảng bằng $\sqrt{2} - 1$ ?
Chỗ nhập nội dung câu trả lời tự luận
Câu 20: Vận dụng

Trong hệ trục toạ độ $(Oxy)$ , cho đồ thị hàm số $(C):y = \frac{x^{2} + x + 1}{x + 1}$ với $x > - 1$ mô tả chuyển động của một chiếc thuyền trên biển. Một trạm phát sóng đặt tại điểm $I( - 1; - 1)$ , biết hoành độ điểm $M$ thuộc đồ thị $(C)$ mà tại đó thuyền thu được sóng tốt nhất là $x_{0} = \frac{1}{\sqrt[n]{a}} - b$ (loại trừ các điều kiện ảnh hưởng đến việc thu phát sóng). Tính giá trị biểu thức $P = a.n + b$ ?

Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Trong hệ trục toạ độ $(Oxy)$ , cho đồ thị hàm số $(C):y = \frac{x^{2} + x + 1}{x + 1}$ với $x > - 1$ mô tả chuyển động của một chiếc thuyền trên biển. Một trạm phát sóng đặt tại điểm $I( - 1; - 1)$ , biết hoành độ điểm $M$ thuộc đồ thị $(C)$ mà tại đó thuyền thu được sóng tốt nhất là $x_{0} = \frac{1}{\sqrt[n]{a}} - b$ (loại trừ các điều kiện ảnh hưởng đến việc thu phát sóng). Tính giá trị biểu thức $P = a.n + b$ ?

Chỗ nhập nội dung câu trả lời tự luận
Câu 21: Vận dụng

Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.
Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ $900(km/h)$ lên $920(km/h)$ , trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc $900(km/h)$ và $920(km/h)$ lần lượt biểu diễn bởi hai vectơ $\overrightarrow{F_{1}}$ và $\overrightarrow{F_{2}}$ với $\overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight)$ . Tính giá trị của $k$ (Làm tròn kết quả đến chữ số thập phân thứ hai).
Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.
Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ $900(km/h)$ lên $920(km/h)$ , trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc $900(km/h)$ và $920(km/h)$ lần lượt biểu diễn bởi hai vectơ $\overrightarrow{F_{1}}$ và $\overrightarrow{F_{2}}$ với $\overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight)$ . Tính giá trị của $k$ (Làm tròn kết quả đến chữ số thập phân thứ hai).
Chỗ nhập nội dung câu trả lời tự luận
Câu 22: Vận dụng cao

Có tất cả bao nhiêu giá trị nguyên của tham số $m \in ( - 2021;2021)$ để hàm số $y = \left| x^{4} - 4x^{2} + m + 2020ight|$ có 7 điểm cực trị?
Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Có tất cả bao nhiêu giá trị nguyên của tham số $m \in ( - 2021;2021)$ để hàm số $y = \left| x^{4} - 4x^{2} + m + 2020ight|$ có 7 điểm cực trị?
Chỗ nhập nội dung câu trả lời tự luận

3 lượt xem

Sắp xếp theo

Xóa Gửi bình luận

Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo Đề 5

Chúc mừng Bạn đã hoàn thành bài!