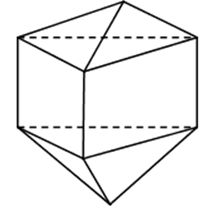
Cho hình lăng trụ ![]() có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của
có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của ![]() lên mặt phẳng
lên mặt phẳng ![]() trùng với trung điểm
trùng với trung điểm ![]() của
của ![]() . Góc tạo bởi cạnh bên
. Góc tạo bởi cạnh bên ![]() với mặt đáy là
với mặt đáy là ![]() . Tính thể tích khối trụ
. Tính thể tích khối trụ ![]() .
.
3 || Ba || ba || V=3
Cho hình lăng trụ có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của
lên mặt phẳng
trùng với trung điểm
của
. Góc tạo bởi cạnh bên
với mặt đáy là
. Tính thể tích khối trụ
.
3 || Ba || ba || V=3
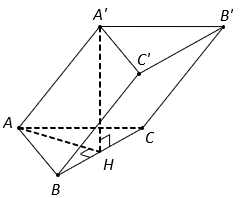
Tam giác đều ABC cạnh bằng 2 nên .
Vì nên hình chiếu vuông góc của
trên mặt đáy
là AH.
Do đó .
Suy ra tam giác vuông cân tại H nên
.
Diện tích tam giác đều ABC là .
Vậy .









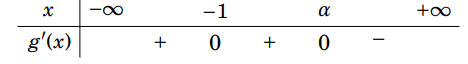
 . Khi đó m + n bằng:
. Khi đó m + n bằng: